pytorch:线性回归实战
pytorch:线性回归实战
- 数学原理
- pytorch实现
数学原理
首先我们看一下什么是线性回归,直观的看就是一张图上有很多散列的点
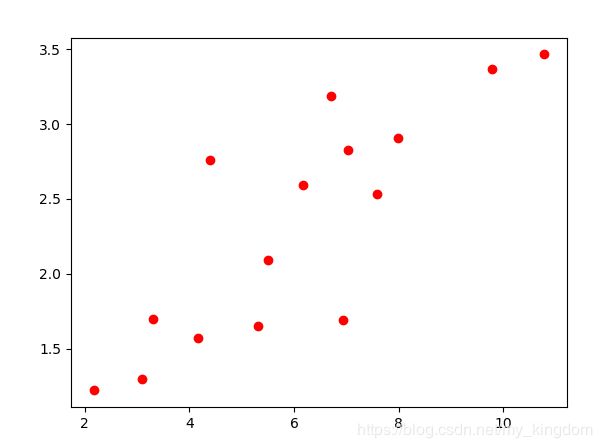
我们要找一个函数来描述这种关系,而线性回归的话表示我们要找一个形如:
f ( x ) = w ∗ x + b f(x)=w*x+b f(x)=w∗x+b
这样的函数来描述这样关系,也可以写成:
f ( x ) = w 1 ∗ x 1 + w 2 ∗ x 2 f(x)=w_1*x_1+w_2*x_2 f(x)=w1∗x1+w2∗x2
其中 x 1 = 1 x_1=1 x1=1
而如果写成矩阵的形式的话,就是:
f ( x ) = W X T f(x)=WX^T f(x)=WXT
其中:
W = ( w 2 , w 1 ) , X = ( x 2 , 1 ) W=(w_2,w_1),X=(x_2,1) W=(w2,w1),X=(x2,1)
因此问题就变成了,求最优w,使损失函数最小,损失函数用均方误差(MSE)来描述,即:
l o s s = 1 2 ∗ ( y ^ − y ) 2 loss=\frac{1}{2}*(\hat{y}-y)^2 loss=21∗(y^−y)2
其中y hat 表示预测的y值,y表示真实的y值。
最优w求解是使用梯度下降算法,通过对凸函数loss求导,另一阶导等于0,得到w的最优值,详细推倒可以参考西瓜数和吴恩达的视频讲解。
最后得到如下结果图:

pytorch实现
使用pytoch实现起来很简单,按照数学的思路,我们的实现也大致分为:1.定义好函数,在pytoch中使用torch.nn.Linear实现。2.定义好损失函数,pytorch里面有MSE函数可用。3.使用梯度下降优化得到最优w,pytorch里面同样有现成函数实现。其他都是一些象加载数据,处理数据,画图显示这样的旁线操作。把握住数学推倒过程这一主线,拿pytorch给你造好的轮子快速实现。
完整代码如下:
import torch as t
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
import numpy as np
lr = 0.01
num_epochs = 100
in_size = 1
out_size = 1
# Toy dataset
x_train = np.array([[3.3], [4.4], [5.5], [6.71], [6.93], [4.168],
[9.779], [6.182], [7.59], [2.167], [7.042],
[10.791], [5.313], [7.997], [3.1]], dtype=np.float32)
y_train = np.array([[1.7], [2.76], [2.09], [3.19], [1.694], [1.573],
[3.366], [2.596], [2.53], [1.221], [2.827],
[3.465], [1.65], [2.904], [1.3]], dtype=np.float32)
#define function,can accomplish using a line code: model= nn.Linear(in_size, out_size)
class LinerRegression(nn.Module):
def __init__(self, in_size, out_size):
super(LinerRegression, self).__init__()
self.fc1 = nn.Linear(in_size, out_size)
def forward(self, x):
y_hat = self.fc1(x)
return y_hat
model = LinerRegression(in_size, out_size)
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=lr)
for epoch in range(num_epochs):
x = t.from_numpy(x_train)
y = t.from_numpy(y_train)
y_hat = model(x)
loss = criterion(y_hat, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
print("[{}/{}] loss:{:.4f}".format(epoch+1, num_epochs, loss))
#plot graph
y_pred = model(t.from_numpy(x_train)).detach().numpy()
plt.plot(x_train, y_train, 'ro', label='Original Data')
plt.plot(x_train, y_pred, 'b-', label='Fitted Line')
plt.legend()
plt.show()