保边平滑滤波器之双边滤波理论学习

双边滤波那些事

双边滤波是接触到计算摄影领域后觉得比较经典的保边滤波器，一直都想好好学习一下保边平滑相关的算法，现在终于痛下决心来写博客记录下自己的学习历程，也希望看到这篇博客的小伙伴能多多指教！
双边滤波在保边平滑滤波领域可以算是鼻祖了，是1998年发表在IEEE上的一篇文章，原文链接：Bilateral Filter

前言

在介绍保边平滑滤波之前，先回顾下低通滤波。

低通滤波器，顾名思义，就是允许低频信号通过，截断高频信号的滤波器。

高斯滤波（gauss filter）

—— 图像处理邻域最具代表性的低通滤波器

基本思想：当前位置处的滤波结果为以其为窗口中心点，整个窗口内所有像素点的一个加权平均的结果，其中，窗口中邻域点的滤波权重由邻域点和当前点之间的距离所决定，距离越远的邻域点像素值的权重越小。

特点：显然，这种滤波器不关心图像内容，不管是边缘区域还是平坦区域，只要两个点的位置关系不变，滤波器权重都不变。因此，此类滤波器对边缘区域并不具备保留作用，

然而，在人类的视觉系统中，对图像中的梯度信息是十分敏感的。因此，具有保边平滑性质的滤波器在图像处理领域得到了很好的发展。

保边平滑滤波，顾名思义，就是在对图像进行平滑的同时，能够保留边缘信息；

双边滤波（bilateral filter）

——一种基于邻域像素点非线性结合实现保边滤波的滤波器；非迭代型，局部，简单，主要是对像素值和空间距离相似度较高的像素点进行滤波；

如何实现平滑的同时保留边缘？

双边滤波的基本思想是这样的：当前位置处的滤波结果为以其为窗口中心点，整个窗口内所有像素点的一个加权平均的结果。与高斯滤波不同的是： 窗口中邻域点的滤波权重由1）邻域点和当前点之间的距离以及2）这两个像素点之间的像素值差异所决定。距离越远，像素值差越大的邻域点像素值对当前位置滤波结果的影响权重越小。

双边滤波基础理论

同上，先列出熟悉的灰度图像高斯滤波的理论公式：

g(x,y)=∑(i,j)∈Ωwg(i,j)f(i,j)∑(i,j)∈Ωwg(i,j) g ( x , y ) = ∑ ( i , j ) ∈ Ω w g ( i , j ) f ( i , j ) ∑ ( i , j ) ∈ Ω w g ( i , j )

其中， (i,j) ( i , j ) 为以 (x,y) ( x , y ) 为中心 r r 为半径的方形窗口内的所有元素, 权重 wg(i,j) w g ( i , j ) 的定义如下：

wg(i,j)=exp(−||(i,j)−(x,y)||22σ2) w g ( i , j ) = exp ⁡ ( − | | ( i , j ) − ( x , y ) | | 2 2 σ 2 )

而灰度图像的双边滤波的定义如下：

g(x,y)=∑(i,j)∈Ωwb(i,j)f(i,j)∑(i,j)∈Ωwb(i,j) g ( x , y ) = ∑ ( i , j ) ∈ Ω w b ( i , j ) f ( i , j ) ∑ ( i , j ) ∈ Ω w b ( i , j )

其中， (i,j) ( i , j ) 为以 (x,y) ( x , y ) 为中心 r r 为半径的方形窗口内的所有元素, 和高斯滤波不同的是：双边滤波权重 wb(i,j) w b ( i , j ) 的定义如下：

wb(i,j)=exp(−||(i,j)−(x,y)||22σ2d−||f(i,j)−f(x,y)||22σ2c) w b ( i , j ) = exp ⁡ ( − | | ( i , j ) − ( x , y ) | | 2 2 σ d 2 − | | f ( i , j ) − f ( x , y ) | | 2 2 σ c 2 )

——双边滤波器可看作由一个空间滤波器和一个颜色滤波器构成

从上面的公式明显可以看出：

1. 两种滤波算法的总框架一致，均为加权平均；双边滤波的权重由像素点间的空间距离和颜色距离共同决定，而高斯滤波的权重仅由空间距离所决定，这也就决定了前者具有保边平滑特性，而后者不具；

2. 两种算法的计算复杂度因权重计算的不同有着较大差异；高斯滤波因其线性性质，算法复杂度可从 O(N2) O ( N 2 ) 降至 O(N) O ( N ) ；而作为一种非线性滤波器的双边滤波，从上述公式可以看出，其复杂度为 O(rN2) O ( r N 2 ) ；其中， N N 为待滤波图像的像素点数， r r 为滤波窗口尺寸。

因此，双边滤波复杂度的降低就成为后来学者的关注重点，相关论文以后会慢慢分析，接下来结合上述公式从其在灰度图像以及彩色图像的应用分析其特性。

双边滤波特性分析

考虑在边缘附近使用bilateral filter，则会有下图的一个效果：

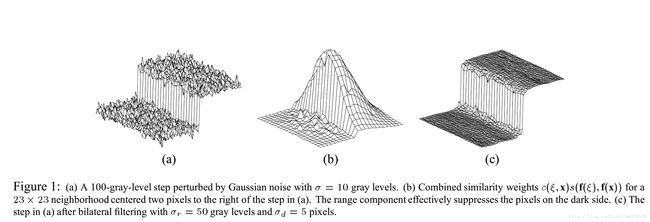
当在遇到图(a)所示的待滤波区域时，一个窗口为23 * 23的双边滤波权重如图(b)所示。

结果：

对边缘处的像素点进行滤波时，窗口中边缘上的点权重较大，边缘外的点，权重趋于零，经过滤波后，即可保持边缘处像素点的值；
对非边缘处的像素点进行滤波时，窗口中的像素点和权重相当，滤波以后的图像得到平滑；
由此，双边滤波后的结果如上图(c)所示。

双边滤波作用于灰度图

NOTE:此算法可用于在图像传输，图片编辑操作以及用在检索领域的图像描述等做数据降维

上图展示的是在不同的 σr σ r 和 σd σ d 的设置下，双边滤波的结果

从上图可以看出：

对于一张灰度图，

• σr σ r 取100或300时，对于 σd=1 σ d = 1 的情况影响较小，此时，空间滤波器可看作一个标准的高斯滤波器，如右上角图片所示；
• σr σ r 取值较小时，整个滤波器就体现出来保边平滑性，如左上角图像所示；
• σd=10 σ d = 10 ， σr σ r 较大的情况，一些细节被平滑了，如右下角图所示。

双边滤波作用于彩色图

在处理彩色图像时，传统算法通常会有新的颜色(artifacts)产生，比如下图中的图(c), 是在对边缘进行平滑的时候产生的，看上去会有些突兀：

而双边滤波可以避免这个问题，在滤波的时候，双边滤波可以合理的将三个通道的像素融合起来，并在此空间对像素距离进行度量。

结论

1. 双边滤波的可推广性极强，甚至可以定义一个新的尺度空间， σr σ r 作相应的尺度变换即可，在这个空间中增加 σr σ r ，即可保边平滑细节

   Perhaps even a new scale space can be defined in which the range filter parameter σr σ r corresponds to scale. In such a space, detail is lost for increasing σr σ r , but edges are preserved at all range scales that are below the maximum image intensity value.

2. 比起线性滤波，双边滤波的复杂度较高，其复杂度优化成为后来保边平滑滤波领域一个重要的研究方向。

---

以上就是自己关于双边滤波的学习笔记，为了更加深入的理解双边滤波的“双边性”，下一篇博客会记录双边滤波的实现以及不同参数下的滤波效果。

版权归原作者所有，转载请注明出处！