卷积convolution函数的矩阵化计算方法及其梯度的反向传播

摘要

本文给出卷积 convolution 函数的矩阵化计算方法, 并求解其在反向传播中的梯度

相关

配套代码, 请参考文章 :

Python 实现 TensorFlow 和 PyTorch 验证卷积 convolution 函数矩阵化计算及反向传播

Affine 变换的定义和梯度, 请参考文章 :

affine/linear(仿射/线性)变换函数详解及全连接层反向传播的梯度求导

系列文章索引 :
https://blog.csdn.net/oBrightLamp/article/details/85067981

正文

在本书的前文, 我们给出了卷积函数的定义及其梯度反向传播的计算方法. 为了深入理解卷积的含义, 前文使用的是原生的卷积定义, 编程实现时使用了循环算法. 为了避免过多的循环嵌套造成理解困难, 前文并没有考虑 mini-batch 批处理和多通道卷积算法.

使用卷积的矩阵化计算方法, 可以大大简化批处理和多通道卷积计算的算法实现. 这一方法也有助于理解后面将要介绍的反卷积 (又称转置卷积) 的概念.

因为本书希望以最小的代价理解深度学习的算法原理, 不打算重新造轮子, 这里默认输入的数据已通过合适的 padding 操作和维度相容检查, 不再考虑相关算法的实现. 有兴趣的读者可自行在本文的基础上添加前处理和后处理算法.

1. 主要过程

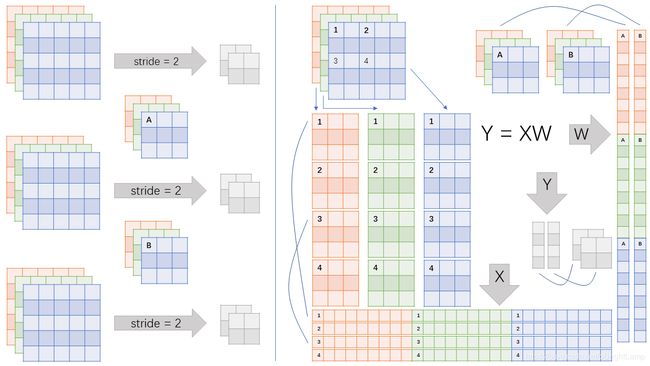
以下图为例, 输入的数据为 3 通道 RGB 彩色图片, 尺寸为 5 x 5, 一个批次共有 3 张图片.

卷积核的同样为 3 通道, 尺寸为 3 x 3, 共有两个.

每一张图片都经过两个卷积核, 卷积的步长为 2, 输出两张 2 x 2 的特征图.

以一张图片为例, 每一个通道按照卷积核的大小, 步长为 2 扫描得到 4 个子矩阵. 相同扫描位置的 3 个通道的子矩阵重排并合并成一个行向量. 共有 4 个扫描位置, 所以有 4 个行向量, 按顺序组成矩阵 X.

对应 3 通道图片的重排顺序, 将每一个卷积核重排成一个列向量, 共有两个列向量, 组成矩阵 W.

通过矩阵乘法可得矩阵 Y, 重排后可得我们需要的两张 2 x 2 的特征图.

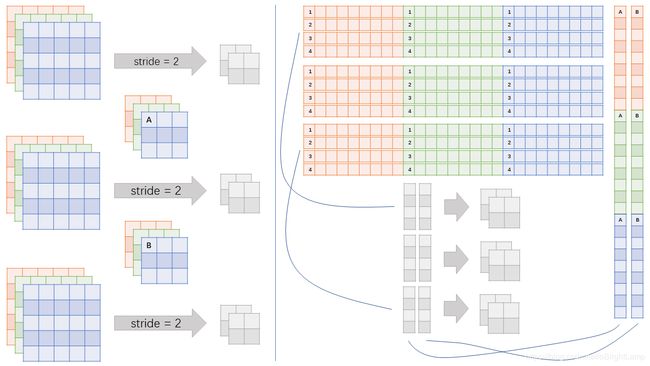
同样的, 一个批次共有 3 张图片, 我们可以将他们组合成一个输入矩阵, 一次性处理.

2. 批处理数据的矩阵化方法

详细的算法请参考配套代码中的 Batch2ConvMatrix 类, 对照上例中的两张图片, 按顺序进行循环遍历即可.

反向传播过程亦类似, 按顺序将相关的梯度传播至批数据的对应位置即可.

卷积的扫描位置若有重叠, 将该位置的梯度相加即可.

3. 矩阵化后的卷积运算及其反向传播

从上面的讨论可知, 对批数据和卷积和矩阵化后, 卷积运算可以使用下式表示 :
$$Y=XW+b$$
这是标准的 Affine 函数运算. 其反向梯度的计算方法请参考本书的相关文章.

全文完.