智能计算作业——BP网络拟合单变量函数
下面是很简单的一个BP网络的例子,来人呐,快来人抄我作业呀╭(╯^╰)╮
问题描述:
用BP网络逼近任意单变量函数。
算法理论:我百科上帮你们抄下来啦╭(╯^╰)╮
BP神经网络是一种按误差反向传播(简称误差反传)训练的多层前馈网络,其算法称为BP算法,它的基本思想是梯度下降法,利用梯度搜索技术,以期使网络的实际输出值和期望输出值的误差均方差为最小。
求解步骤:
利用MATLAB自带函数建立BP网络。
——输入求解问题
——初始化网络net=newff([-2*pi2*pi],[str2double(get(handles.edit1,'String')) 1],{'tansig','tansig'},'traingdx');
——训练网络 net.trainParam.xx()
——测试网络 sim(net,X);
运行结果:
运行bp.m文件,弹出交互界面:
预设该网络为三层BP网络,一层隐含层,求解函数自行输入(输入格式要符合MATLAB语句格式)。以拟合函数y = sin(x)+cos(x)为例,探究隐含层神经元个数对拟合效果的影响。
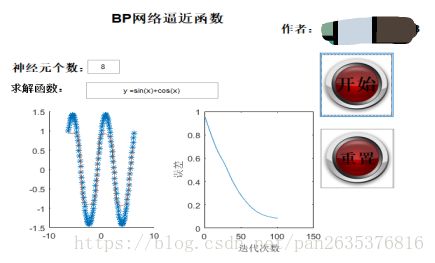
输入y = sin(x)+cos(x),神经元个数为8,点击“开始”,结果如下:
预设该网络为三层BP网络,一层隐含层,求解函数自行输入(输入格式要符合MATLAB语句格式)。以拟合函数y = sin(x)+cos(x)为例,探究隐含层神经元个数对拟合效果的影响。(蓝色星号为原函数,红色连线为拟合函数线)。
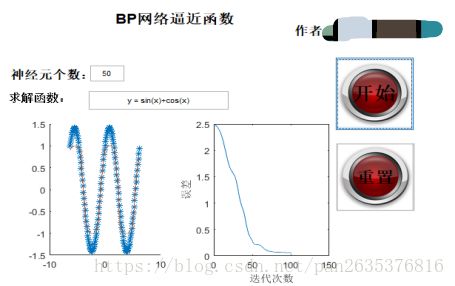
点击“重置”,神经元个数为50,结果如下:
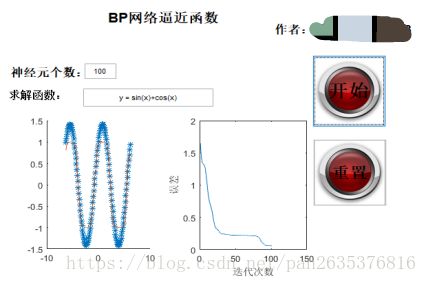
点击“重置”,神经元个数为100,结果如下:
实验总结:
隐含层神经元从8到50到100,隐含层神经元越多,误差越低,收敛速度越快。
我写不出什么花来,你们自己总结一下吧╭(╯^╰)╮
思考:
虽然隐含层神经元越多,拟合效果越好,但是过多的隐含层神经元可能造成过拟合,在测试拟合新的函数时效果变差。
思考不要抄我╭(╯^╰)╮你得自己想
程序如下:
readme.txt文件了解一下╭(╯^╰)╮这个写上,方便老师使用,会显得你专业一点
% BP网络逼近单变量函数
% 姓名:
% 学号:
% 邮箱:
% 环境: MATLABR2017A
% 日期: 2018.10.7
% 运行说明: 运行bp.m即可弹出图形交互界面bp.gui
点击“运行”按钮即可运行程序;
输入神经元个数,如:8
输入要逼近的函数(要求符合MATLAB格式),如:y = exp(x)+sin(x)
点击“重置”按钮恢复;
主程序:bp.m
function varargout = bp(varargin)
%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% BP网络逼近单变量函数
% 姓名:
% 学号:
% 邮箱:
% 环境: MATLABR2017A
% 日期: 2018.10.7
%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
gui_Singleton = 1;
gui_State = struct('gui_Name', mfilename, ...
'gui_Singleton', gui_Singleton, ...
'gui_OpeningFcn', @bp_OpeningFcn, ...
'gui_OutputFcn', @bp_OutputFcn, ...
'gui_LayoutFcn', [], ...
'gui_Callback', []);
if nargin && ischar(varargin{1})
gui_State.gui_Callback = str2func(varargin{1});
end
if nargout
[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});
else
gui_mainfcn(gui_State, varargin{:});
end
function bp_OpeningFcn(hObject, eventdata, handles, varargin)
handles.output = hObject;
A = imread('A.jpg');
A = imresize(A,[100,100]);
set(handles.kaishi,'CData',A);
set(handles.rek,'CData',A);
guidata(hObject, handles);
function varargout = bp_OutputFcn(hObject, eventdata, handles)
varargout{1} = handles.output;
function kaishi_Callback(hObject, eventdata, handles)
X = -2*pi:0.1:2*pi;
D = value(handles.edit2,X);
% D = eval(get(handles.edit2,'String'));
net = newff([-2*pi 2*pi],[str2double(get(handles.edit1,'String')) 1],{'tansig','tansig'},'traingdx');
box on;
net.trainParam.epochs = 100; %训练的最大次数
net.trainParam.goal = 0.005; %全局最小误差
[net tr] = train(net,X,D);
O = sim(net,X);
axes(handles.axes1);
plot(X,D,'*',X,O); %绘制训练后得到的结果和误差曲线
axes(handles.axes2);
a = 1:101;
plot(a,tr.perf);
xlabel('迭代次数');
ylabel('误差');
% V = net.iw{1,1}%输入层到中间层权值
% theta1 = net.b{1}%中间层各神经元阈值
% W = net.lw{2,1}%中间层到输出层权值
% theta2 = net.b{2}%输出层各神经元阈值
function rek_Callback(hObject, eventdata, handles)
cla(handles.axes1);
cla(handles.axes2);
set(handles.edit1,'String','');
set(handles.edit2,'String','');
function edit1_Callback(hObject, eventdata, handles)
function edit1_CreateFcn(hObject, eventdata, handles)
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
set(hObject,'BackgroundColor','white');
end
function traingdx_Callback(hObject, eventdata, handles)
function edit2_Callback(hObject, eventdata, handles)
function edit2_CreateFcn(hObject, eventdata, handles)
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
set(hObject,'BackgroundColor','white');
end
还有一个value.m文件,这个里面写的是要求解的函数,在主程序里调用,复制下来,你不用运行它╭(╯^╰)╮:
function y = value(t,x)
eval(get(t,'String'));
end还有一张图,跟上一篇文章一样,这个是GUI界面的按钮的图╭(╯^╰)╮一定要保存在代码路径下,命名为‘A.png’,不然会报错: