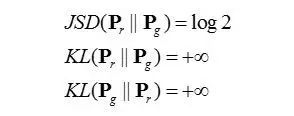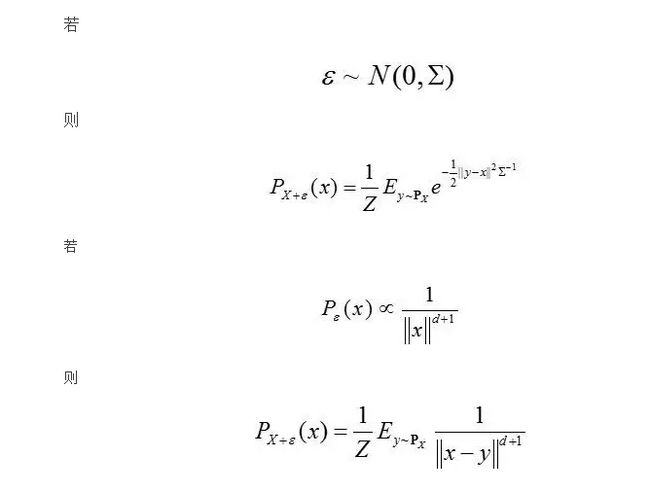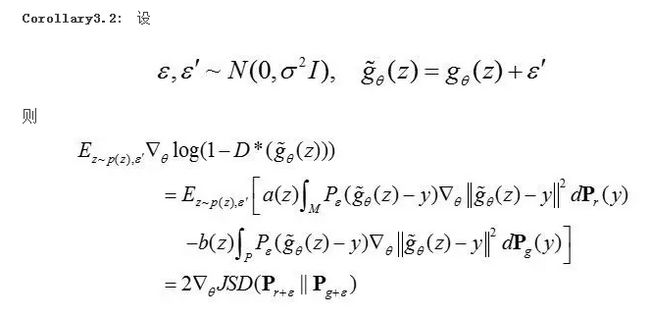Wasserste GAN理解
原文:发布者: 炼数成金_小数 原作者: Gapeng
GAN回顾
GAN回顾
Martin 称这个loss为original cost function(参见[1] 2.2.1章节),而实际操作中采用的loss为the –log D cost(参见[1] 2.2.2章节)。
GAN存在的问题:初探
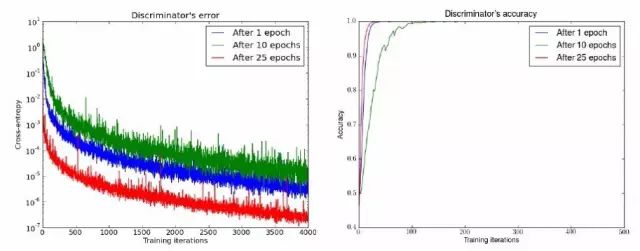
当固定G时,训练D直到收敛,可以发现D的loss会越来越小,趋于0,这表明JSD(Pr || Pg)被最大化了,并且趋于log2。如下图所示。
而这会导致什么问题呢?在实践中人们发现,当D训练得更精确,G的更新会变得越差,训练变得异常地不稳定。为什么会产生这些这样的问题?之前一直没有人给出解答。
JSD(Pr || Pg)达到最大化,有两种可能:
概率分布不是(绝对)连续的,也就是说,它没有密度函数。我们常见的分布一般都有密度函数。如果概率分布是定义在一个低维的流形上(维度低于全空间),那它就不是绝对连续的。
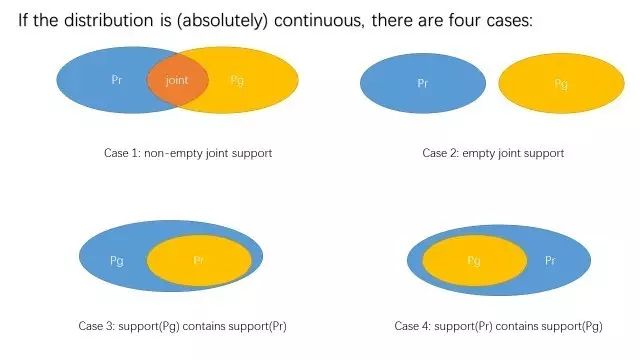
分布是绝对连续的,但是两者的支撑集没有交集。两个分布的支撑集不外乎包含以下四种情形:
经过计算可以发现(参见下期推送),case1 的JSD小于log2,case2的JSD等于log2,case3和4的JSD也不超过log2。实际上这很好理解,两个分布差异越大,交叉熵越大。
这是比较直观的解释,更进一步地,作者从理论上进行了严格的分析和证明。
GAN存在的问题:理论分析
Lemma 1:设
是一个由仿射变换和逐点定义的非线性函数(ReLU、leaky ReLU或者诸如sigmoid、tanh、softplus之类的光滑严格递增函数)复合得到的复合函数,则g(Z)包含在可数多个流形的并集中,并且它的维数至多为dim(Z)。因此,若dim(Z) < dim(X),则g(Z)在X中测度为0。
Lemma1表明,若generator(G)是一个 神经网络,并且G的输入(随机高斯噪声)的维数比产生的图像的维数低,则无论怎样训练,G也只能产生整个图像空间中很小的部分,有多小呢?它在图像空间中只是一个零测集。零测集是什么概念呢,举些例子,二维空间中的一条直线、三维空间中的一个平面。二维平面在三维空间中是没有“厚度”的,它的体积是0。
我们训练GAN时,训练集总归是有限的,Pr一般可以看成是低维的流形;如果Pg也是低维流形,或者它与Pr的支撑集没有交集,则在discriminator (D)达到最优时,JSD就会被最大化。D达到最优将导致G的梯度变得异常地差,训练将变得异常不稳定。
下面的几个定理、引理就是在证明Pg在上述两种情况下,最优的D是存在的。
Theorem2.1: 若分布Pr和Pg的支撑集分别包含在两个无交紧致子集M和P中,则存在一个光滑的最优discriminator D*: X -> [0,1],它的精度是1,并且,对任意的
定理2.1是什么意思呢?如果两个概率分布的支撑集没有交集,则完美的D总是存在的,并且(在两个分布的支撑集的并集上)D的梯度为0,也就是说,这时候任何梯度 算法都将失效。这就是GAN训练的时候,(在两个概率分布的支撑集没有交集的情况下)当D训练效果很好的时候,G的更新将变得很差的原因。
Lemma2: 设M和P是R^d的两个非满维度的正则子流形,再设η 和 η’ 是任意的两个独立连续随机变量,定义两个扰动流形M’ = M + η,P’ = P + η’,则
Lemma 2是为定理2.2做准备,它表明任意两个非满维的正则子流形都可以通过微小的扰动使得它们不是完美对齐(notperfectly align)的,即它们的交点都是横截相交(intersect transversally)的。横截相交和完美对齐的严谨定义将在下期推送中给出,在这里形象地说明一下:
横截相交(intersect transversally):对两个子流形,在任意一个交点处,两者的切平面能够生成整个空间,则称两个子流形横截相交。当然,如果它们没有交集,则根据定义,它们天然就是横截相交的。下图给出了一个示例,在交点P处,平面的切平面是其自身,直线的切平面也是其自身,它们可以张成全空间,因此是横截相交的,而两个直线没办法张成全空间,因此不是横截相交的;如果两个流形是相切的,在切点处它们的切平面是相同的,也不可能张成全空间,因此也不是横截相交的。
完美对齐(perfectly align): 如果两个子流形有交集,并且在某个交点处,它们不是横截相交的。
Pr和Pg的支撑集如果存在交集,那么根据lemma2,我们总可以通过微小的扰动使得它们不是完美对齐的,也就是说,它们是横截相交的。
Lemma3: 设M和P是R^d的两个非完美对齐,非满维的正则子流形,L=M∩P,若M和P无界,则L也是一个流形,且维数严格低于M和P的维数。若它们有界,则L是至多四个维数严格低于全空间的流形之并。无论哪种情形,L在M或者P中的测度均为0。
Lemma 3说的是,两个正则子流形(满足一定条件:非完美对齐,非满维)的交集的维数要严格低于它们自身的维数。也就是说,它们的交集只是冰山一角,小到相对它们自身可以忽略。对于Pr和Pg的支撑集来说,根据Lemma 2,我们总可以通过微小扰动使得它们是非完美对齐的,在根据Lemma 3,Pr和Pg的交集是微不足道。
Theorem2.2: 设Pr和Pg分别是支撑集包含在闭流形M和P中的两个分布,且它们非完美对齐、非满维。进一步地,我们假设Pr和Pg在各自的流形中分别连续,即:若集合A在M中测度为0,则Pr(A) = 0(在Pg上也有类似结果)。则存在精度为1的最优discriminator D*: X->[0,1],并且几乎对M 或者P中的任意点x,D*在x的任意邻域内总是光滑的,且有
定理2.1证明的是对于Pr和Pg无交的情形下,最优的discriminator是存在的。定理2.2承接Lemma 3,它证明了在Pr和Pg的支撑集有交集,且横截相交的情况下,最优的discriminator是存在的。这两个定理实际上把两种可能导致D最优,且梯度消失的情形在理论上做出证明,由于梯度的消失,G的更新将得不到足够的梯度,导致G很差。
Theorem2.3: 在定理2.2的条件下,有
定理2.3表明,随着D越来越好,D的loss将越来越小,趋于0,因此Pr和Pg的JSD被最大化,达到最大值log2,这时,Pr和Pg的交叉熵达到无穷大,也就是说,即使两个分布之间的差异任意地小,它们之间的KL散度仍然会被最大化,趋于无穷。这是什么意思呢?利用KL散度来衡量分布间的相似性在这里并不是一个好的选择。因此,我们有必要寻求一个更好的衡量指标。
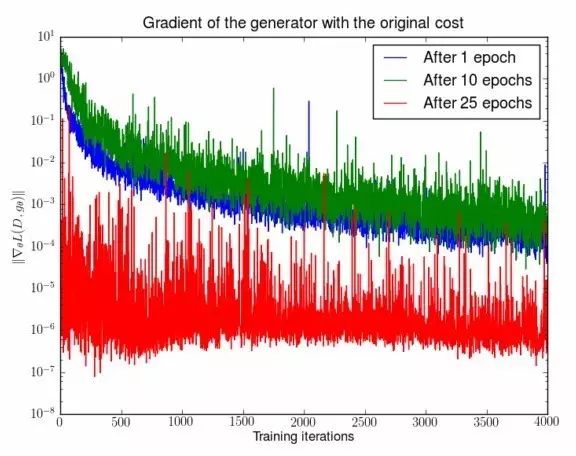
定理2.4 探究了generator在前面所述情况下回出现什么问题,它从理论上给出了,若G采用original cost function(零和博弈),那么它的梯度的上界被D与最优的D*之间的距离bound住。说人话就是,我们训练GAN的时候,D越接近最优的D*,则G的梯度就越小,如果梯度太小了,梯度算法不能引导G变得更好。下图给出了G的梯度变化(固定G,训练D),注意到随着训练的进行,D将变得越来越精确,这时G的梯度强度将变得越来越小,与理论分析符合。
定理2.5研究了G的loss为the –logD cost时将会出现的问题。我们可以看到,当JSD越大时,G的梯度反而会越小,也就是说,它可能会引导两个分布往相异的方向,此外,上式的KL项虽对产生无意义图像会有很大的惩罚,但是对mode collapse惩罚很小,也就是说,GAN训练时很容易落入局部最优,产生mode collapse。KL散度不是对称的,但JSD是对称的,因此JSD并不能改变这种状况。这就是我们在训练GAN时经常出现mode collapse的原因。
定理2.6告诉我们,若G采用the –logD cost,在定理2.1或者2.2的条件下,当D与D*足够接近时,G的梯度会呈现强烈震荡,这也就是说,G的更新会变得很差,可能导致GAN训练不稳定。
下图给出了定理2.6的实验模拟的效果,在DCGAN尚未收敛时,固定G,训练D将导致G的梯度产生强烈震荡。当DCGAN收敛时,这种震荡得到有效的抑制。
既然general GAN采用的loss不是一种好的选择,有什么loss能够有效避免这种情形吗?
一个临时解决方案
一个可行的方案是打破定理的条件,给D的输入添加噪声。后续的几个定理对此作了回答。
定理3.1和推论3.1表明,ε的分布会影响我们对距离的选择。
定理3.2证明了G的梯度可以分为两项,第一项表明,G会被引导向真实数据分布移动,第二项表明,G会被引导向概率很高的生成样本远离。作者指出,上述的梯度格式具有一个很严重的问题,那就是由于g(Z)是零测集,D在优化时将忽略该集合;然而G却只在该集合上进行优化。进一步地,这将导致D极度容易受到生成样本的影响,产生没有意义的样本。
Wasserstein距离
定义3.1: X上的两个分布P、Q的Wasserstein度量W(P,Q)定义为
其中,Г是X×X上所有具有边界分布P和Q的联合分布集。
Wasserstein距离通常也称为转移度量或者EM距离(地动距离),它表示从一个分布转移成另一个分布所需的最小代价。下图给出了一个离散分布下的例子,将f1(x)迁移成f2(x)最小代价即是移动f1(x)在最大值处的2个单位的概率到最小值处,这样就得到了分布f2(x)。更复杂的离散情形需要通过求解规划问题。
定理3.3告诉我们一个有趣的事实,上式右边两项均能被控制。第一项可以通过逐步减小噪声来逐步减小;第二项可以通过训练GAN(给D的输入添加噪声)来最小化。
作者指出,这种通过给D的输入添加噪声的解决方案具有一大好处,那就是我们不需要再担心训练过程。由于引入了噪声,我们可以训练D直到最优而不会遇到G的梯度消失或者训练不稳定的问题,此时G的梯度可以通过推论3.2给出。
总而言之,WGAN的前传从理论上研究了GAN训练过程中经常出现的两大问题:G的梯度消失、训练不稳定。并且提出了利用地动距离来衡量Pr和Pg的相似性、对D的输入引入噪声来解决GAN的两大问题,作者证明了地动距离具有上界,并且上界可以通过有效的措施逐步减小。
这可以说是一个临时性的解决方案,作者甚至没有给出实验进行验证。在WGAN[2]这篇文章中,作者提出了更完善的解决方案,并且做了实验进行验证。下面我们就来看一下这篇文章。
Wasserstein GAN
常见距离
Martin Arjovsky在WGAN论文进一步论述了为什么选择Wasserstein距离(地动距离)。
设X是一个紧致度量空间,我们这里讨论的图像空间([0,1]^d)就是紧致度量空间。用Σ表示X上的所有博雷尔集,用Prob(X)表示定义在X上的概率度量空间。给定Prob(X)上的两个分布Pr, Pg,我们可以定义它们的距离/散度(请注意:散度不是距离,它不是对称的。距离和散度都可以用于衡量两个分布的相似程度):
表示以Pr, Pg为边缘分布的所有联合分布组成的集合。
我们用一个简单的例子来看一下这四种距离/散度是怎么计算的。
考虑下图的两个均匀分布:
二维平面上,P1是沿着y轴的[0,1]区间上的均匀分布,P2是沿着x=θ,在y轴的[0,1]区间上的均匀分布。简而言之,你可以把P1和P2看成是两条平行的线段。容易计算
当θ->0时,W->0,然而TV距离、KL散度、JS散度都不收敛。也就是说,地动距离对某些情况下要更合理一些。更严谨的结论由下面的定理给出。
PS: 为了统一编号,后续的定理编号与原文[2]的编号不一样,两种编号相差3...
3. 上述两个结论对JS散度和KL散度均不成立。
定理4表明,地动距离与JS散度、KL散度相比,具有更好的性质。
WGAN
采用Wasserstein距离作为loss的GAN称为WassersteinGAN,一般简写为WGAN。直接考虑Wasserstein距离需要算inf,计算是很困难的。考虑它的Kantorovich-Rubinstein对偶形式
可以看到,如果把GAN的目标函数的log去掉,则两者只相差一个常数,也就是说,WGAN在训练的时候与GAN几乎一样,除了loss计算的时候不取对数!Loss function中的对数函数导致了GAN训练的不稳定!
WGAN实验
作者发现,如果WGAN训练采用SGD或者RMSProp算法,则收敛效果很好。一般不采用基于momentum的算法,如Adam算法,实现观察发现这类优化算法会导致训练变得不稳定。而我们知道,DCGAN采用Adam算法进行优化效果会比较好。这是WGAN与GAN训练方法的差别。
此外,WGAN当前的loss(Wasserstein距离)能够用于指示训练的效果,即G产生的图像质量,Wasserstein距离越小,G产生的图像质量就越高。先前的GAN由于训练不稳定,我们很难通过loss去判断G产生的质量(先前的GAN的loss大小并不能表明产生图像质量的高低)。这个发现对于训练GAN有很大的帮助。
此外,WGAN如果采用DCGAN架构去训练,产生的图像质量效果与DCGAN没有明显差异;并且,即使generator采用MLP(多层感知机),仍然能够产生质量不错的图像。实验结果如下图所示(图中的曲线不会跟GAN一样产生强烈震荡了!)。
此外,作者指出,WGAN的实验中并没有发现mode collapse!
WGAN代码及材料
Reddit讨论区传送门:
https://www.reddit.com/r/MachineLearning/comments/5qxoaz/r_170107875_wasserstein_gan/?from=groupmessage
推荐一篇用更通俗易懂的语言介绍WGAN的文章:
https://zhuanlan.zhihu.com/p/25071913
WGAN源码,作者提供,Torch版本:
https://github.com/martinarjovsky/WassersteinGAN
Tensorflow版本:https://github.com/Zardinality/WGAN-tensorflow
Keras版本:
https://github.com/tdeboissiere/DeepLearningImplementations/tree/master/WassersteinGAN
参考文献
Arjovsky, M., & Bottou, L.eon. (2017). Towards Principled Methods for Training Generative AdversarialNetworks.
Arjovsky, M., Soumith, C.,& Bottou, L. eon. (n.d.). Wasserstein GAN.