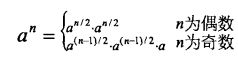【剑指offer】面试题16：数值的整数次方

题目：实现函数 double Power(double base, int exponent)，求 base 的 exponent 次方。不得使用库函数，同时不需要考虑大数问题。

•  1、自以为很简单的解法

 由于不需要考虑大数问题，这道题看起来很简单，可能不少应聘者在看到题目30秒后就能写出如下的代码：

public double powerWithExponent(double base,int exponent){
    double result = 1.0;
    for(int i = 1; i <= exponent; i++){
        result = result*base;
    }
    return result;
}

不过遗憾的是，写的快不一定就能得到面试官的青睐，因为面试官会问输入的指数（exponent）小于1（零和负数）的时候怎么办？上面的代码完全没有考虑，只包括了指数为正数的情况。

• 2、全面但不够高效的解法，我们离Offer已经很近了

我们知道当指数为负数的时候，可以先对指数求绝对值，然后算出次方的结果之后再取倒数。既然有求倒数，我们很自然的就要想到有没有可能对0求倒数，如果对0求倒数怎么办？当底数base是零且指数是负数的时候，如果不做特殊的处理，就会出现对0求倒数，从而导致程序运行出错。怎么告诉函数的调用者出现了这种错误？在Java中可以抛出异常来解决。

最后需要指出的是，由于0的0次方在数学上没有意义的，因此无论是输出0还是1都是可以接收的，但这都需要和面试官说清楚，表明我们已经考虑到了这个边界值了。

有了这些相对而言已经全面很多的考虑，我们就可以把最初的代码修改如下：

// 数值的整数次方
public class Power {

	public double power(double base, int exponent){
		double result = 0.0;
		if(equal(base, 0.0) && exponent < 0){
			throw new IllegalArgumentException("0的负数次幂无意义");
		}
		// 任何数的0次幂都是0
		if(equal(exponent, 0)){
			return 1.0;
		}
		// 当指数小于0的时候，先对指数取绝对值，算出次方的结果之后再取倒数
		if(exponent < 0){
			result = powerWithExponent(1.0 / base, -exponent);
		}else{
			result = powerWithExponent(base, exponent);
		}
		return result;
	}

	private double powerWithExponent(double base, int exponent) {
		double result = 1.0;
		for (int i = 0; i < exponent; i++) {
			result = result * base;
		}
		return result;
	}

	// 判断两个double型数据是否相等，计算机有误差
	private boolean equal(double n1, double n2) {
		if((n1 - n2 > -0.0000001) && (n1 - n2 < 0.0000001)){
			return true;
		}else{
			return false;
		}
	}
	
	// 测试
	public static void main(String[] args) {
		Power power = new Power();
		System.out.println(power.power(3, -1));   // 0.3333333333333333
		System.out.println(power.power(3, 0));    // 1.0
		System.out.println(power.power(3, 2));    // 9.0
	}
}

由于计算机表示小数（包括float和double型小数）都会有误差，我们不能直接用等号（==）判断两个小数是否相等。如果两个小数的差的绝对值很小，比如小于0.0000001，就可以认为他们相等。

此时我们考虑得已经很周详了，已经能够得到很多面试官的要求了。但是如果我们碰到的面试官是一个在效率上追求完美的人，那么他有可能提醒我们函数PowerWithExponent还有更快的办法。

• 3、全面而高效的解法，确保我们能拿到Offer

如果输入的指数exponent为32，我们在函数powerWithExponent的循环中需要做31次乘方。但我们可以换一种思路考虑：我们的目标是求出一个数字的32次方，如果我们已经知道了它的16次方，那么只要16次放的基础上再平方一次就可以了。而16次方又是8次方的平方。这样以此类推，我们求32次方只需要5次乘方：先求平方，在平方的基础上求4次方，在4次方的基础上求8次方，在8次方的基础上求16次方，最后在16此方的基础上求32次方。

也就是说我们可以利用下面这个公示求 a 的 n 次方：

这个公式就是我们前面利用O(logn)时间求斐波那契数列时，讨论的公式，这个公式很容易就能用递归实现。新的PowerWithExponent代码如下：

public class Power {

	public double power(double base, int exponent){
		double result = 0.0;
		if(equal(base, 0.0) && exponent < 0){
			throw new IllegalArgumentException("0的负数次幂无意义");
		}
		// 任何数的0次幂都是0
		if(equal(exponent, 0)){
			return 1.0;
		}
		// 当指数小于0的时候，先对指数取绝对值，算出次方的结果之后再取倒数
		if(exponent < 0){
			result = powerWithExponent(1.0 / base, -exponent);
		}else{
			result = powerWithExponent(base, exponent);
		}
		return result;
	}
	
	// 更高效
	private double powerWithExponent(double base, int exponent){
		if(exponent == 0){
			return 1;
		}
		if(exponent == 1){
			return base;
		}
		
		double result = powerWithExponent2(base, exponent >> 1);
		result *= result;
        // 0x代表16进制
		if((exponent & 0x1) == 1){
			result *= base;
		}
		return result;
	}

	// 判断两个double型数据是否相等，计算机有误差
	private boolean equal(double n1, double n2) {
		if((n1 - n2 > -0.0000001) && (n1 - n2 < 0.0000001)){
			return true;
		}else{
			return false;
		}
	}
	
	// 测试
	public static void main(String[] args) {
		Power power = new Power();
		System.out.println(power.power(3, -1));   // 0.3333333333333333
		System.out.println(power.power(3, 0));    // 1.0
		System.out.println(power.power(3, 2));    // 9.0
	}
}

最后再提醒一个细节：我们用右移运算代替除2，用位与运算符代替了求余运算符（%)来判断一个数是奇数还是偶数。位运算的效率比乘除法及求余运算的效率要高很多。既然要优化代码，我们就把优化做到极致。

• 另一种实现方法【来自牛客网】

https://www.nowcoder.com/questionTerminal/1a834e5e3e1a4b7ba251417554e07c00

1、全面考察指数的正负、底数是否为零等情况。

2、写出指数的二进制表达，例如13表达为二进制1101。

3、举例:10^1101 = 10^0001*10^0100*10^1000。

4、通过&1和>>1来逐位读取1101，为1时将该位代表的乘数累乘到最终结果。

public class PowerNum {

	/**
	 * 1.全面考察指数的正负、底数是否为零等情况。
	 * 2.写出指数的二进制表达，例如13表达为二进制1101。
	 * 3.举例:10^1101 = 10^0001*10^0100*10^1000。
	 * 4.通过&1和>>1来逐位读取1101，为1时将该位代表的乘数累乘到最终结果。
	 */
	public double power(double base, int n){
		double result = 1, current = base;
		int exponent;
		if(n > 0){
			exponent = n;
		}else if(n < 0){
			// 底数等于0
			if(base == 0){
				throw new RuntimeException("分母不能为0");
			}
			exponent = -n;
		}else{
			// n = 0 的情况
			return 1;
		}
		
		while(exponent != 0){
			// 如果当前exponent的最右位为1
			if((exponent & 1) == 1){
				result *= current;
			}
			// 如果当前exponent的最右位为0
			current *= current;  // 翻倍
			exponent >>= 1;      // 右移一位
		}
		// 如果n小于0，需要返回result的倒数
		return n >= 0 ? result : (1 / result);
	}
	
	// 测试
	public static void main(String[] args) {
		PowerNum pn = new PowerNum();
		System.out.println(pn.power(2, 2));   // 4.0
		System.out.println(pn.power(2, -1));  // 0.5
		System.out.println(pn.power(2, 0));   // 1.0
	}
}