梯度下降法(BGD,SGD,MSGD)python+numpy具体实现
梯度下降是一阶迭代优化算法。为了使用梯度下降找到函数的局部最小值,一个步骤与当前位置的函数的梯度(或近似梯度)的负值成正比。如果相反,一个步骤与梯度的正数成比例,则接近该函数的局部最大值;该程序随后被称为梯度上升。梯度下降也被称为最陡峭的下降,或最快下降的方法。(from wikipad)
首先,大家要明白它的本质:这是一个优化算法!!!它是可以用来解决很多问题的,一般学习机器学习的朋友都会在线性回归的遇到这个名词,但是要声明的是,它和最小二乘法类似,是用于求解线性回归问题的一种方法。同时它的功能又不仅于此,它在线性回归中的意义在于通过寻找梯度最大的方向下降(或上升)来找到损失函数最小时候对应的参数值。
好了,绕来绕去的就拿线性回归的例子来和大家讲讲吧。
梯度下降方法
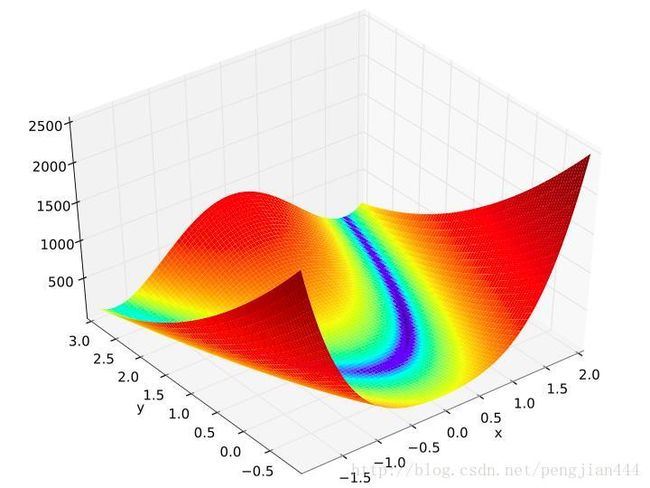
本质是每次迭代的时候都沿着梯度最大的地方更新参数。现在假设有函数(Rosenbrock函数:是一个用来测试最优化算法性能的非凸函数,由Howard Harry Rosenbrock在1960年提出[1]。也称为Rosenbrock山谷或Rosenbrock香蕉函数,也简称为香蕉函数)如下定义:
f(x,y)=(1−x)2+100(y−x2)2
很明显,其最小最为 f(1,1)=0 ,其三维图片如下:
函数 f 分别对 x , y 求导得到
∂f(x,y)∂x=−2(1−x)−2∗100(y−x2)∗2x
∂f(x,y)∂y=2∗100(y−x2)
在实现的过程中可以给出x, y初始值(例如设置为 0, 0) 然后计算函数在这个点的梯度,并按照梯度方向更新x, y的值。
这里给出通过梯度下降法计算上述函数的最小值对应的x 和 y
import numpy as np
def cal_rosenbrock(x1, x2):
"""
计算rosenbrock函数的值
:param x1:
:param x2:
:return:
"""
return (1 - x1) ** 2 + 100 * (x2 - x1 ** 2) ** 2
def cal_rosenbrock_prax(x1, x2):
"""
对x1求偏导
"""
return -2 + 2 * x1 - 400 * (x2 - x1 ** 2) * x1
def cal_rosenbrock_pray(x1, x2):
"""
对x2求偏导
"""
return 200 * (x2 - x1 ** 2)
def for_rosenbrock_func(max_iter_count=100000, step_size=0.001):
pre_x = np.zeros((2,), dtype=np.float32)
loss = 10
iter_count = 0
while loss > 0.001 and iter_count < max_iter_count:
error = np.zeros((2,), dtype=np.float32)
error[0] = cal_rosenbrock_prax(pre_x[0], pre_x[1])
error[1] = cal_rosenbrock_pray(pre_x[0], pre_x[1])
for j in range(2):
pre_x[j] -= step_size * error[j]
loss = cal_rosenbrock(pre_x[0], pre_x[1]) # 最小值为0
print("iter_count: ", iter_count, "the loss:", loss)
iter_count += 1
return pre_x
if __name__ == '__main__':
w = for_rosenbrock_func()
print(w)如果大家想运行这个算法,建议使用默认的参数,效果还不错。不要把step_size设置过大,会出问题的(可能是实现过程有问题,请指正)。
线性回归问题
这里关于回归的前导介绍我建议大家取看周志华老师的西瓜书,介绍得通透明亮,但是周老师对线性回归问题给出的解决方法是通过最小二乘法来做的,而我们在这里要用梯度下降。
这里给出一般的定义吧~
一般的线性回归方程如下:
y=θ1∗x1+θ2∗x2+⋯+θn∗xn+b
转换为:
y=θ1∗x1+θ2∗x2+⋯+θn∗xn+θ0∗b
这里 θ0=1 转换为向量的形式 y=θT∗x , θ , x ,均为为行向量。
现在需要定义损函数,用于判断最后得到的预测参数的预测效果。常用的损失函数是均方误差:
J(θ)=12m∑j=1m(h(θ)i−yi)2
i 是维度索引 j 是样本索引,接下来对 θ 求导得到
∂J(θ)∂θj=1m∑j=1m(h(θ)i−yi)xij
更新公式为:
θi=θi−α1m∑j=1m(h(θ)i−yi)xij
α 就是学习的步长。
BGM(批量梯度下降法)
import numpy as np
def gen_line_data(sample_num=100):
"""
y = 3*x1 + 4*x2
:return:
"""
x1 = np.linspace(0, 9, sample_num)
x2 = np.linspace(4, 13, sample_num)
x = np.concatenate(([x1], [x2]), axis=0).T
y = np.dot(x, np.array([3, 4]).T) # y 列向量
return x, y
def bgd(samples, y, step_size=0.01, max_iter_count=10000):
sample_num, dim = samples.shape
y = y.flatten()
w = np.ones((dim,), dtype=np.float32)
loss = 10
iter_count = 0
while loss > 0.001 and iter_count < max_iter_count:
loss = 0
error = np.zeros((dim,), dtype=np.float32)
for i in range(sample_num):
predict_y = np.dot(w.T, samples[i])
for j in range(dim):
error[j] += (y[i] - predict_y) * samples[i][j]
for j in range(dim):
w[j] += step_size * error[j] / sample_num
for i in range(sample_num):
predict_y = np.dot(w.T, samples[i])
error = (1 / (sample_num * dim)) * np.power((predict_y - y[i]), 2)
loss += error
print("iter_count: ", iter_count, "the loss:", loss)
iter_count += 1
return w
if __name__ == '__main__':
samples, y = gen_line_data()
w = bgd(samples, y)
print(w) # 会很接近[3, 4]SGB(随机梯度下降法)
import numpy as np
def gen_line_data(sample_num=100):
"""
y = 3*x1 + 4*x2
:return:
"""
x1 = np.linspace(0, 9, sample_num)
x2 = np.linspace(4, 13, sample_num)
x = np.concatenate(([x1], [x2]), axis=0).T
y = np.dot(x, np.array([3, 4]).T) # y 列向量
return x, y
def sgd(samples, y, step_size=0.01, max_iter_count=10000):
"""
随机梯度下降法
:param samples: 样本
:param y: 结果value
:param step_size: 每一接迭代的步长
:param max_iter_count: 最大的迭代次数
:param batch_size: 随机选取的相对于总样本的大小
:return:
"""
sample_num, dim = samples.shape
y = y.flatten()
w = np.ones((dim,), dtype=np.float32)
loss = 10
iter_count = 0
while loss > 0.001 and iter_count < max_iter_count:
loss = 0
error = np.zeros((dim,), dtype=np.float32)
for i in range(sample_num):
predict_y = np.dot(w.T, samples[i])
for j in range(dim):
error[j] += (y[i] - predict_y) * samples[i][j]
w[j] += step_size * error[j] / sample_num
# for j in range(dim):
# w[j] += step_size * error[j] / sample_num
for i in range(sample_num):
predict_y = np.dot(w.T, samples[i])
error = (1 / (sample_num * dim)) * np.power((predict_y - y[i]), 2)
loss += error
print("iter_count: ", iter_count, "the loss:", loss)
iter_count += 1
return w
if __name__ == '__main__':
samples, y = gen_line_data()
w = sgd(samples, y)
print(w) # 会很接近[3, 4]MBGB(小批量梯度下降法)
import numpy as np
import random
def gen_line_data(sample_num=100):
"""
y = 3*x1 + 4*x2
:return:
"""
x1 = np.linspace(0, 9, sample_num)
x2 = np.linspace(4, 13, sample_num)
x = np.concatenate(([x1], [x2]), axis=0).T
y = np.dot(x, np.array([3, 4]).T) # y 列向量
return x, y
def mbgd(samples, y, step_size=0.01, max_iter_count=10000, batch_size=0.2):
"""
MBGD(Mini-batch gradient descent)小批量梯度下降:每次迭代使用b组样本
:param samples:
:param y:
:param step_size:
:param max_iter_count:
:param batch_size:
:return:
"""
sample_num, dim = samples.shape
y = y.flatten()
w = np.ones((dim,), dtype=np.float32)
# batch_size = np.ceil(sample_num * batch_size)
loss = 10
iter_count = 0
while loss > 0.001 and iter_count < max_iter_count:
loss = 0
error = np.zeros((dim,), dtype=np.float32)
# batch_samples, batch_y = select_random_samples(samples, y,
# batch_size)
index = random.sample(range(sample_num),
int(np.ceil(sample_num * batch_size)))
batch_samples = samples[index]
batch_y = y[index]
for i in range(len(batch_samples)):
predict_y = np.dot(w.T, batch_samples[i])
for j in range(dim):
error[j] += (batch_y[i] - predict_y) * batch_samples[i][j]
for j in range(dim):
w[j] += step_size * error[j] / sample_num
for i in range(sample_num):
predict_y = np.dot(w.T, samples[i])
error = (1 / (sample_num * dim)) * np.power((predict_y - y[i]), 2)
loss += error
print("iter_count: ", iter_count, "the loss:", loss)
iter_count += 1
return w
if __name__ == '__main__':
samples, y = gen_line_data()
w = mbgd(samples, y)
print(w) # 会很接近[3, 4]