不产生候选集的关联规则挖掘算法FP-Tree

上篇博客讲述了Apriori算法的思想和Java实现，http://blog.csdn.NET/u010498696/article/details/45641719 Apriori算法是经典的关联规则算法，但是如上篇博客所述，它也有两个致命的性能瓶颈，一个是频繁集自连接产生候选集这一步骤中可能产生大量的候选集；另一个是从候选集得到频繁项集需要重复扫描数据库。

2000年，Han等提出了一个称为FP-tree的算法，有效解决了以上两个问题，它只需要扫描数据库2次，并不使用候选集，通过构造一棵频繁模式树（Pattern frequent tree,FP-Tree），将所有数据库信息压缩到频繁模式树上，最后通过这棵树生成关联规则。

FP-tree算法主要步骤，1：利用数据库中的数据构造FP-Tree；2：从FP-Tree中挖掘频繁模式。下面先给出算法描述，再举例说明。

---------------------------------------------------------------------------------------------------------------------------------------------------------

算法：FP-Tree 挖掘频繁模式

输入：事务数据库D；最小支持度阈值min_sup.

输出：频繁模式

方法：1.构造FP-Tree

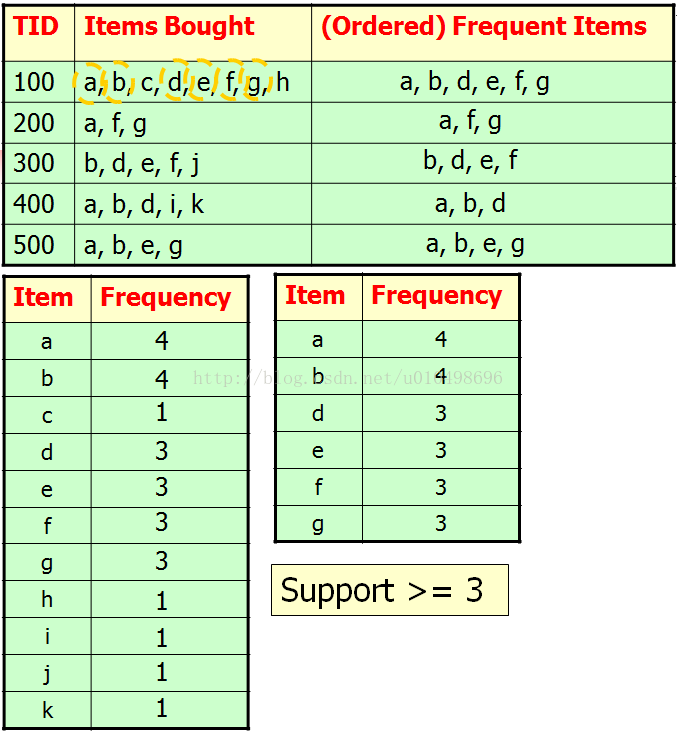
（a）扫描数据库第一次，得到频繁一项集F1，并对F按支持度度排序。-----除了要排序，这一步和Apriori得到频繁一项集完全相同。

（b）创建FP-Tree根节点，以root标记，对于事务数据库D中的每个事务执行如下操作：

选择每个事务中的频繁项并按支持度排序，设排序后的频繁项表为[p|P]，其中p是第一个元素，P为剩余元素的表。调用Insert_tree([p|P],root)将p插入到树  中，直到频繁项表为空。

    2.挖掘FP-Tree

precedure FP-Tree(Tree,a)

if Tree 含有单个路径P then

for路径P中节点的每个组合（记为b）do

产生模式 bUa，其中support=b中节点的最小支持度

else for each ai 在FP-Tree的项头表

产生一个模式b = aiUa， 其支持度support = ai.support；

构造b的条件模式基，然后构造b的条件FP-Tree Tree b；

if Tree b 不为空集   then   call FP_Tree(Tree b,b); 

----------------------------------------------------------------------------------------------------------------------------------------------------------

算法：Insert_tree([p|P],root) 将频繁项[p|P]插入到频繁模式树root中

输入：待插入频繁项[p|P]    FP-tree树root

输出：FP-tree树root

方法：   if（root有孩子child节点使得child.name = p.name）

then child.count++;  //节点child的支持度加1

else

创建新节点，将其支持度置1，链接到其父节点root，并链接到与其具有相同节点名的节点；

-----------------------------------------------------------------------------------------------------------------------------------------------------------

显然 FP-Tree算法只需要扫描数据库2次，第一次是生成频繁1项集，第二次是根据频繁1项集，对数据库中每个元组，将其项目集中的关联和频度信息放入FP-Tree中。

在频繁模式树的构造过程中，总是将出现频度高的项放在更靠近根节点的地方，这样构造的树才是紧凑的，在频繁模式的挖掘过程中，是从项头表的最后一项，也就是1项频繁集中的最不频繁项开始挖掘，直到第一项为止。

FP-Tree树结构优点：1完整性，保留了频繁模式挖掘的完整信息，不会破坏任何一个事务的长模式

2紧致性，减少了非相关信息（非频繁项被丢弃）不会比原始数据库大。

java实现中，节点类的定义如下：

 public class TreeNode  {
     private String name; // 节点名称
     private int count; // 计数
     private TreeNode parent; // 父节点
     private List children; // 子节点
     private TreeNode nextHomonym; // 下一个同名节点
     //方法略
     ...
 }

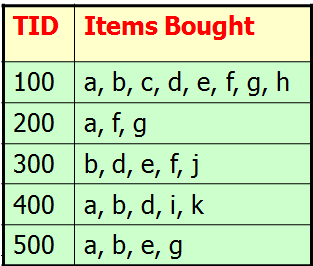
下面举例说明，对于如下数据库中的数据：

第一次扫面数据库，得到按支持度排序的频繁1项集

下面构造FP-Tree，依次从第一行开始，将每一个事务中的频繁项加入到树中。

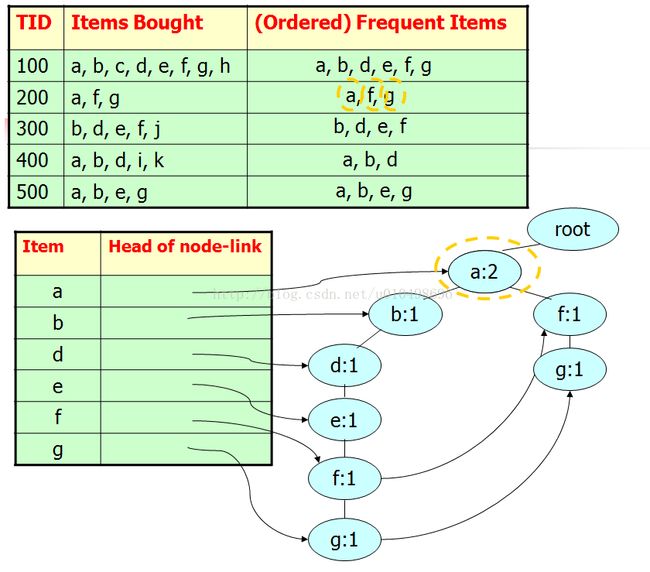
如下图为加入TID=100事务后构造的树。先加入a节点，再一次b，d，e，f，g

如下图，添加完第一个行数据后，形成树的一条分支，下面继续添加第二行，a，f，g。由于已经有a节点，所以并不需要新建节点，只需要将原来节点a的支持度+1变为2即可

添加 f 时，a的孩子中没有f节点，故新建f节点，置支持度为1，以f节点为根继续添加g节点。添加完后如下所示：

依次类推，将剩下的事务添加到树中，形成如下FP-tree

5个事务共形成4条分支，并且表头节点形成链表，连接所有节点名相同的所有结点。下面进行挖掘过程：

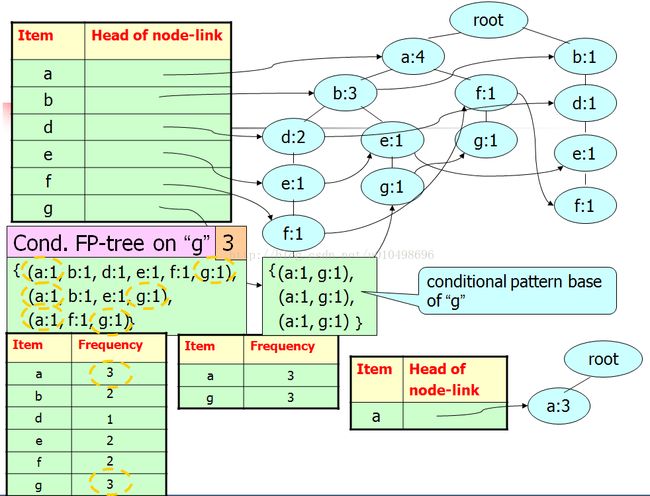
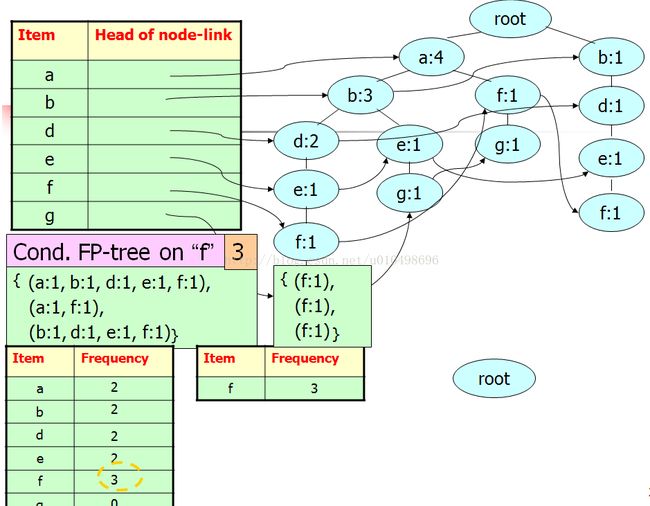
首先从最不频繁的频繁项g节点开始，寻找g的条件模式基（由FP-tree中以g节点结束的所有从根节点到g的路径组成）

如下图所示：以g结束的路径共有3条，计算每个节点出现的支持度，大于等于3的只有a节点

所以g节点的条件模式基只有节点a

在寻找节点f的条件模式基如下：为空

依次寻找 e d b a节点的条件模式基，汇总如下：

最后，得到的频繁模式如下

支持度为3

支持度为3

支持度为3

支持度为3

总结：FP-Tree方法将发现长频繁模式的问题转换成递归发现一些短模式，然后与后缀连接。它使用最不频繁项作为后缀，提供了好的选择性。该方法大大降低了搜索开销。

主要问题有

1）在挖掘频繁模式时，它需要递归地生成条件FP-tree，并且每产生一个频繁模式就要生成一个条件FP-tree。

2）在支持度阀值较小时，即使对于很小的数据库，也将产生数以十万计的频繁模式。动态的生成和释放数以十万计的条件FP-树，将耗费大量时间和空间。

3）此外，FP-tree和条件FP-tree需要自顶向下生成，而频繁模式的挖掘需要自底向上处理。由于递归地生成条件FP-树，因此FP-树和条件FP-树必须双向可遍历。这样，        FP-tree和条件FP-tree的节点中就需要更多的指针，从而需要更大的内存空间来维护FP-tree和条件FP-tree。

关于FP-Tree算法的java实现可见博客：http://www.cnblogs.com/zhangchaoyang/articles/2198946.html

参考文献《数据挖掘概念与技术》 Jiawei Han Micheline Kamber

转载：http://blog.csdn.net/u010498696/article/details/45817689