栈的应用--简单计算器转换知识
栈的应用
1. 表达式求值
- 1.问题描述:
这里限定的表达式求值问题是:用户输入一个包含“+”、“-”、“*”、“/”、正整数和圆括号的合法数学表达式,计算该表达式的运算结果。 - 2.数据组织
算术表达式exp采用字符数组表示,其中只含有“+”、“-”、“*”、“/”、正整数和圆括号。
为了方便,假设该表达式都是合法的数学表达式,例如,exp=”1+2*(4+12)”;在设计相关算法中用到栈,这里采用顺序栈存储结构。 - 3.设计运算算法
了解一下算术表达式:
这里所谓的前缀,中缀,后缀是根据操作符的位置来定的,如果操作符在操作数前面,则称为前缀表达式,例如“- + 1 × + 2 3 4 5”;如果操作符在操作数之间,则称为中缀表达式,例如
“1+((2+3)×4)-5”;如果操作符在操作数后面,则称为后缀表达式,例如“1 2 3 + 4 × + 5 -”。
(一):讲一下将中缀表达式转化为后缀表达式
①.虽然中缀表达式符合人类的日常思维习惯,但是计算机在存储中缀表达式时,需要使用树这种数据结构,如果表达式过于复杂,那么树的高度会变得很高,大大增加了时间复杂度和空间复杂度。如果转换成线性结构,那么效率将变得高很多,所以需要将中缀表达式先转换成前缀或者后缀表达式,然后依靠栈这种线性数据结构来进行计算。
②.前缀表达式又叫波兰表达式,后缀表达式又叫逆波兰表达式。前缀表达式基本没有在商业计算机中使用过,所以现实中用的更多的是后缀表达式。
③. 如何将中缀表达式转化成后缀表达式呢?
- 利用两个栈S1,S2:其中S1存放操作符,S2存放操作数
1.从左往右遍历中缀表达式,如果遇到数字,则放入S2中,如果遇到操作符,则放入S1中。
2.在放操作符的时候有一定的规则,如果栈为空或栈顶元素为”(“,则直接压栈。如果是(,也直接压栈;
3.如果栈顶元素为普通操作符,则比较优先级,如果待压栈的操作符比栈顶操作符优先级高,则直接压栈,否则(如果待压栈的操作符比栈顶操作符优先级低或则相等)将S1中的栈顶元素出栈,并压入S2中,再接着往下比较S1栈顶元素的优先级。
4.如果遇到”)”,则依次弹出S1栈顶的运算符,并压入S2,直到遇到左括号”(“为止,此时将这一对括号丢弃。
5.最后将S1中剩余的运算符依次弹出并压入S2,逆序输出S2(从栈底到栈顶)便得到了后缀表达式。(注意:等号的优先级最低,因为要到最后才进行赋值操作)
④.得到后缀表达式之后,计算就变得方便多了,遇到数字就压栈,遇到操作符的时候,pop出栈顶的两个元素,进行计算后将结果又压入栈中,这样一直下去,直到得到最终结果。
将中缀表达式“1+((2+3)×4)-5”转换为后缀表达式的过程如下:
因此结果为“1 2 3 + 4 × + 5 -”(需要逆序输出)
(二)再讲一下将中缀表达式转化为前缀表达式:
中缀表达式转换前缀表达式其实过程和转换后缀表达式及其相似,只是对其中的几个不同之处稍微说明一下:
1 转换后缀表达式由于符号是要在操作数后面出现,所以操作数入栈,扫描顺序是从左向右,转换前缀表达式的话操作符需要在操作数前面出现,那么扫描顺序就应该是从右向左。
2 操作符的具体处理方式和转换到后缀表达式略有不同,括号的操作也是’)’直接入栈,’)’则配对’(’后一起出栈
3.在输出的时候,直接按照正常的栈输出即可,而后缀表达式则需逆序输出。
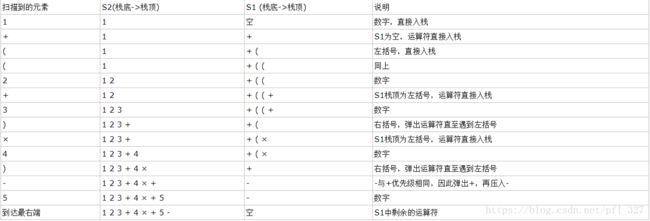
利用两个栈S1,S2:其中S1存放操作符,S2存放操作数
| 扫描到的元素 | S2 栈底->栈顶 | S1 栈底->栈顶 |
|---|---|---|
| 5 | 5 | 空 |
| - | 5 | - |
| ) | 5 | -,) |
| 4 | 5,4 | -,) |
| * | 5,4 | -,),* |
| ) | 5,4 | -,),*,) |
| 3 | 5,4,3 | -,),*,) |
| + | 5,4,3 | -,),*,),+ |
| 2 | 5,4,3,2 | -,),*,),+ |
| ( | 5,4,3,2,+ | -,),* |
| ( | 5,4,3,2,+,* | - |
| + | 5,4,3,2,+,*,- | + |
| 1 | 5,4,3,2,+,*,-,1 | + |
| 最右端 | 5,4,3,2,+,*,-,1,+ | 空 |
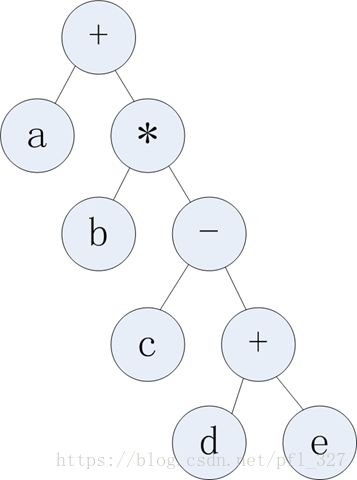
前缀,中缀,后缀表达式与二叉树的表示
这三个表达式其实与二叉树是有这很紧密的联系的,a+b*c-(d+e)这个中缀表达式我们将其操作符当做内节点,操作数当做叶子节点,这样的话就能够画出这个中缀表达式所对应的二叉树
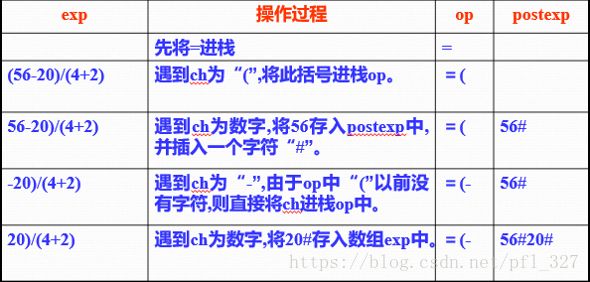
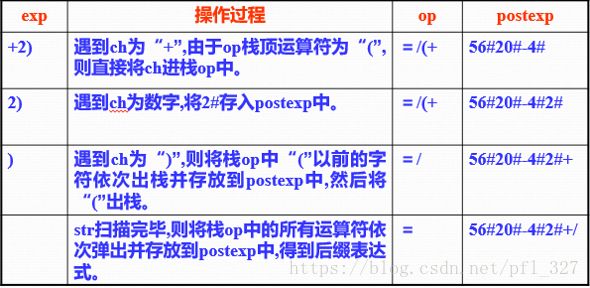
例: 对于表达式“(56-20)/(4+2)”,将其转换成后缀表达式
初始化运算符栈op;
将'='进栈;
从exp读取字符ch;
while (ch!='\0')
{ if (ch不为运算符)
将后续的所有数字均依次存放到postexp中,并以字符'#'标志数值串结束;
else
switch(Precede(op栈顶运算符,ch))
{
case '<': //栈顶运算符优先级低
将ch进栈; 从exp读取下字符ch; break;
case '=': //只有栈顶运算符为'(',ch为')'的情况
退栈; 从exp读取下字符ch; break;
case '>': //栈顶运算符应先执行,所以出栈并存放到postexp中
退栈运算符并将其存放到postexp中; break;
}
}
若字符串exp扫描完毕,则将运算符栈op中'='之前的所有运算符依次出栈并存放到postexp中。最后得到后缀表达式postexp;
- 代码实现:
void trans(char *exp,char postexp[]) /*将算术表达式exp转换成后缀表达式postexp*/
{
char e;
SqStack *Optr; /*定义运算符指针*/
InitStack(Optr); /*初始化运算符栈*/
int i=0; /*i作为postexp的下标*/
while(*exp!='\0') /*exp表达式未扫描完时循环*/
{
switch(*exp)
{
case '(': /*判定为左括号*/
Push(Optr,'('); /*左括号进栈*/
exp++; /*继续扫描其他字符*/
break;
case ')': /*判定为又括号*/
Pop(Optr,e); /*出栈元素*/
while(e!='(') /*不为'('时循环*/
{
postexp[i++]=e; /*将e存放到postexp中*/
Pop(Optr,e); /*继续出栈元素*/
}
exp++; /*继续扫描其他字符*/
break;
case '+': /*判定为加或减号*/
case '-':
while(!StackEmpty(Optr)) /*栈不空循环*/
{
GetTop(Optr,e); /*取栈顶元素e*/
if(e!='(') /*e不是'('*/
{
postexp[i++]=e; /*将存放到postexp中*/
Pop(Optr,e); /*出栈元素e*/
}
else
break;
}
Push(Optr,*exp); /*将‘+’或‘-’进栈*/
exp++; /*继续扫描其他字符*/
break;
case '*': /*判定为'*'或'/'号*/
case '/':
while(!StackEmpty(Optr)) /*栈不空循环*/
{
GetTop(Optr); /*取栈顶元素e*/
if(e=='*'||e=='/') /*将栈顶'*'或'/'运算符出栈并存放到postexp中*/
{
postexp[i++]=e; /*将e存放到postexp中*/
Pop(Optr,e); /*出栈元素*/
}
else /*e为非‘*’或‘/’运算符时退出循环*/
break;
}
Push(Optr,*exp); /*将'*'或'/'进栈*/
exp++; /*继续扫描其他字符*/
break;
default:
while(*exp>='0'&&*exp<='9') /*判定为数字字符*/
{
postexp[i++]=*exp;
exp++;
}
postexp[i++]='#'; /*用#标示一个数字串结束*/
}
}
while(!StackEmpty(Optr)) /*此时exp扫描完毕,栈不为空时循环*/
{
Pop(Optr,e); /*出栈元素e*/
postexp[i++]=e; /*将e存放到postexp中*/
}
postexp[i]='\0'; /*给postexp表达式加结束表示*/
DestroyStack(Optr); /*销毁栈*/
}
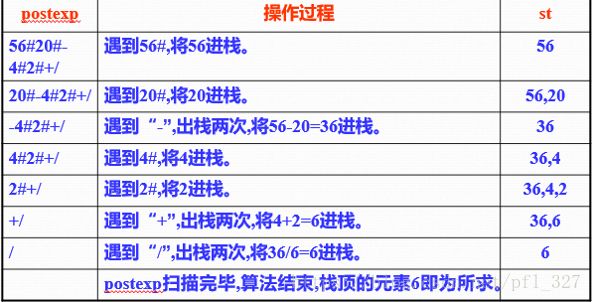
后缀表达式求值。在后缀表达式求值算法中要用到一个数值栈st,该算法实现过程如下:
对后缀表达式求值过程是:从左到右读入后缀表达式,若读入的是一个操作数,就将它入数值栈,若读入的是一个运算符op,就从数值栈中连续出栈两个元素(两个操作数),假设为x和y,计算x op y之值,并将计算结果入数值栈;对整个后缀表达式读入结束时,栈顶元素就是计算结果。对后缀表达式postexp求值伪代码
while (从postexp读取字符ch,ch!='\0')
{ 若ch为数字,将后续的所有数字构成一个整数存放到数值栈st中。
若ch为“+”,则从数值栈st中退栈两个运算数,相加后进栈st中。
若ch为“-”,则从数值栈st中退栈两个运算数,相减后进栈st中。
若ch为“*”,则从数值栈st中退栈两个运算数,相乘后进栈st中。
若ch为“/”,则从数值栈st中退栈两个运算数,相除后进栈st中(若除数为零,则提示相应的错误信息)。
}
若字符串postexp扫描完毕,则数值栈op中的栈顶元素就是表达式的值。
代码:
double compvalue(char *postexp) /*计算后缀表达式的值*/
{
double d,a,b,c,e;
SqStack1 *Opnd; /*定义操作数栈*/
InitStack1(Opnd); /*初始化操作数栈*/
while(*postexp!='\0') /*postexp字符串未扫描完时循环*/
{
switch(*postexp)
{
case '+': /*判定为'+'号*/
Pop1(Opnd,a); /*出栈元素a*/
Pop1(Opnd,b); /*出栈元素b*/
c=b+a; /*计算c*/
Push1(Opnd,c); /*将计算结果c进栈*/
break;
case '-': /*判定为'-'号*/
Pop1(Opnd,a); /*出栈元素a*/
Pop1(Opnd,b); /*出栈元素b*/
c=b-a; /*计算c*/
Push1(Opnd,c); /*将计算结果c进栈*/
break;
case '*': /*判定为'*'号*/
Pop1(Opnd,a); /*出栈元素a*/
Pop1(Opnd,b); /*出栈元素b*/
c=b*a; /*计算c*/
Push1(Opnd,c); /*将计算结果c进栈*/
break;
case '/': /*判定为'/'号*/
Pop1(Opnd,a); /*出栈元素a*/
Pop1(Opnd,b); /*出栈元素b*/
if(a!=0)
{
c=b/a; /*计算c*/
Push1(Opnd,c); /*将计算结果c进栈*/
break;
}
else
{
printf("\n\t除零错误!\n");
exit(0); /*异常退出*/
}
break;
default: /*处理数字字符*/
d=0; /*将连续的数字字符转换成对应的数值存放到d中*/
while(*postexp>='0'&&*postexp<='9') /*判定为数字字符*/
{
d=10*d+*postexp-'0';
postexp++;
}
Push1(Opnd,d); /*将数值d进栈*/
break;
}
postexp++; /*继续处理其他字符*/
}
GetTop1(Opnd,e); /*取栈顶元素e*/
DestroyStack1(Opnd); /*销毁栈*/
return e; /*返回e*/
}- main()主函数代码:
int main()
{
char exp[100];
char postexp[MaxSize];
printf("请输入你想要计算的公式:!!\n");
gets(exp);
trans(exp,postexp); /*将exp转换为postexp*/
printf("中缀表达式:%s\n",exp); /*输出postexp*/
printf("后缀表达式:%s\n",postexp); /*输出postexp的值并输出*/
printf("表达式的值:%g\n",compvalue(postexp)); /*求postexp的值并输出*/
return 1;
}