五子棋AI设计
五子棋AI设计——从门外到门内不得不说的事儿1
这学期选了人工智能原理,上课的时候完全没搞懂老师要讲什么,所以听课听得云里雾里的,幸好有几个小实验,可以帮助理解人工智能的精髓。
第一个实验就是基于带alpha-beta剪枝的MinMax搜索的五子棋AI设计。好久没有写过MFC界面了,所以在pudn上down了几个例程,测试了一下,选了两个比较规范的工程作为开发的基础。
第一天:Naive AI——一个称不上AI的AI
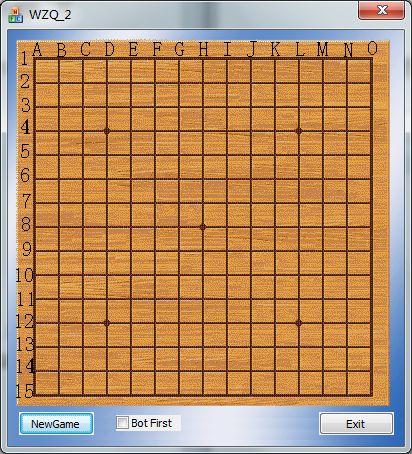
比对着选好的工程进行复制,在复制的过程中删去一些暂时用不到的功能,就搞出了如下界面。
有了棋盘,让我们开始下棋吧。可是这是我还对五子棋的规则一知半解,是个门外汉。只好采用投石问路的方法,先来个简单的吧,随机生成合法落子位置。
首先将棋盘定义为一个整形的二维数组points[16][16],0表示空,1表示黑子,2表示白子。为什么是16,只是觉得用1-15比用0-14直观一些,其实模仿程序是这么定义的。
那么,什么样的位置是合法的呢?就是棋盘上满足points[i][j] == 0的(i,j)。这样随机生成1-15之间的任意整数x = rand()%15 + 1; y =rand()%15 + 1;建议在两个语句中间加若干空循环,避免x和y一样,提高“随机性”,虽然这个随机性并不怎么样吧。
这样,一个称不上AI的AI诞生了,我们就叫他Naive吧。
观赏Naive下棋是一种享受,因为他的表现比我还差,我可以很轻易的在五步之内秒杀他。
在解决了有无问题后,应该着眼于提高AI的水平,使其成为真的AI。
如何提高,路在何方?且听下回分解。
--------------------分割线--------------------
“AI”代码如下,
- void CWuZiQi::Naive( const int points[16][16], bool first, int oldp[16][16], int newp[16][16], int *nx, int *ny )
- {
- int x, y;
- int k = 0;
- // current state quick save
- for ( int i = 1; i <= 15; i++ )
- for ( int j = 1; j <= 15; j++ )
- {
- oldp[i][j] = points[i][j];
- newp[i][j] = points[i][j];
- }
- // place a chess on board
- do
- {
- for ( int j = 0; j < 1000; j++ )
- for ( int k = 0; k < j; k++ )
- ;
- x = rand() % 15 + 1;
- for ( int j = 0; j < 1000; j++ )
- for ( int k = 0; k < j; k++ )
- ;
- y = rand() % 15 + 1;
- k++;
- }while ( oldp[x][y] != 0 || k > 20 );
- if ( k >= 20 )
- {
- *nx = -1; *ny = -1;
- return;
- }
- else
- {
- *nx = x; *ny = y;
- }
- if ( first )
- {
- newp[x][y] = 1;
- }
- else
- {
- newp[x][y] = 2;
- }
- }
五子棋AI设计——从门外到门内不得不说的事儿2
第二天:防守,堵堵堵
为了提高对五子棋游戏的感性认识,我又在网上找了几个写的很好的五子棋游戏,与电脑进行了若干次对弈。作为一个门外汉,防守总是最好的选择。那么在什么条件下防守,在什么位置防守,这些位置如何确定……在这一系列的问题的驱动下,我开始学习模拟对象的AI部分。
首先我选择了总是防守,所以在这一天,我的第一个问题解决了。那么在什么位置放手呢?
之前定义了棋盘用points[i][j]表示,那么最直观的想法是看看棋盘上的棋子,可是棋盘既有白子又有黑子,还有空位。怎么判断呢?好吧,从AI的角度出发,他现在要做的事情是:在当前棋盘状态选择一个合法位置——空位,然后在该位置出招。那么既然是在空位置出招,那么是不是评估棋盘上的空位置来指导出招就可以了?
作为门外汉我现在能够想到的就这么多了,好吧先不管3721,走起。
如何评估棋盘上的空位?
为了大家看起来方便,我先展示一个7*7的棋盘,示意一下。人先执黑,电脑后手执白,现在轮到电脑出招。棋盘如下
1234567
10000000
20000000
30021000
40001000
50000000
60000000
70000000
那么有子周围的空位置中,(2,4)向下看有一个2连,在(5,4)向上看有一个2连,在其他位置看到的都是1连。好了,从防守的角度出发,现在最危险的位置是(2,4)和(5,4)。通过这次观察,我们可以得到一种评估方法,那就是枚举棋盘上的每个空位,然后统计其8个方向上,相同颜色的棋子连成一线的棋子的个数。
为什么是8个方向?
因为空位填上子后,可能将以前的阴线(可能连成一线的线)变成阳线(已经连成一线的线)。因此,我们要在空位置上向八个方向都看看,看看这个位置能够连成多少条阳线,如果连成的阳线越多,阳线中棋子的数目越多,那么这个空位的威胁就越大。
定义int qiju[16][16][8][2]表示棋盘某个位置某个方向某种颜色的棋子连成一线的棋子的个数
定义int a1[16][16], a2[16][16]表示棋盘上某空位的评分。
如何评分呢?我们先考虑一线式的吧,就是横、竖、左斜、右斜这四种。定义int t1 = qiju[i][j][k][0]+qiju[i][j][k+4][0]表示,涵盖了空位在某一方向上一侧或两侧连成一线的棋子数目。
if t1 >= 4 a1[i][j] += 10000000;
if t1 == 3 a1[i][j] += 100000;
if t1 == 2 a1[i][j] += 1000;
if t1 == 1 a1[i][j] += 10;
同理可以计算a2。
好了在a1和a2中找到最大值的位置,如果人执黑,那么AI就用a1的最大值的位置作为落子的位置,如果AI执黑,那么AI就用a2的最大值的位置作为落子的位置。AI就可以成功的封堵住对自己威胁最大的位置,完成防守。
可是AI只会防守怎么行,好吧,那么我们只能重新考虑第一个问题将AI定义为攻守兼备,在什么条件下进攻呢,欲知后事如何,且听下回分解。
--------------------分割线--------------------
AI的代码如下,
- void CWuZiQi::AI_1( const int points[16][16], bool first, int oldp[16][16], int newp[16][16], int *nx, int *ny )
- {
- int i, j;
- int x, y;
- int x1 = 0, x2 = 0, y1 = 0, y2 = 0;
- int qiju[16][16][8][2];
- int a1[16][16], a2[16][16];
- // current state quick save
- for ( i = 1; i <= 15; i++ )
- for ( j = 1; j <= 15; j++ )
- {
- oldp[i][j] = points[i][j];
- newp[i][j] = points[i][j];
- }
- FillMatrix( qiju, 0 );
- FillMatrix( a1, 0 );
- FillMatrix( a2, 0 );
- HowManyInLine( oldp, qiju );
- ValueTheChessboardNaive( oldp, qiju, a1, a2 );
- //rintMatrix( qiju );
- //PrintMatrix( oldp );
- /****************算出分数最高的空位,填写坐标*********************/
- for( i = 1; i <= 15; i++ )
- for( j = 1; j <= 15; j++ )
- {
- if( a1[x1][y1] < a1[i][j] )
- {x1 = i; y1 = j;} // black
- }
- for( i = 1; i <= 15; i++ )
- for( j = 1; j <= 15; j++ )
- {
- if( a2[x2][y2] < a2[i][j] )
- {x2 = i; y2 = j;} // white
- }
- if ( first )
- {
- x = x2;
- y = y2;
- newp[x][y] = 1;
- }
- else
- {
- x = x1;
- y = y1;
- newp[x][y] = 2;
- }
- *nx = x; *ny = y;
- }
统计函数如下,
- void CWuZiQi::HowManyInLine( const int oldp[16][16], int qiju[16][16][8][2] )
- {
- int i, j, k, t, cnt;
- int tx, ty;
- int dx[8] = {0, 1, 1, 1, 0, -1, -1, -1};
- int dy[8] = {-1, -1, 0, 1, 1, 1, 0, -1};
- /****************为双方填写棋型表************/
- for ( i = 1; i <= 15; i++ ) // col
- for ( j = 1; j <= 15; j++ ) // row
- if ( oldp[i][j] == 0 )
- {
- for ( k = 0; k < 8; k++ ) // direction
- {
- // black
- cnt = 0;
- tx = i;
- ty = j;
- for ( t = 0; t < 5; t++ )
- {
- tx += dx[k];
- ty += dy[k];
- if ( tx > 15 || tx < 1 || ty > 15 || ty < 1 )
- break;
- if( oldp[tx][ty] == 1 )
- cnt++;
- else
- break;
- }
- qiju[i][j][k][0] = cnt;
- // white
- cnt = 0;
- tx = i;
- ty = j;
- for ( t = 0; t < 5; t++ )
- {
- tx += dx[k];
- ty += dy[k];
- if ( tx > 15 || tx < 1 || ty > 15 || ty < 1 )
- break;
- if( oldp[tx][ty] == 2 )
- cnt++;
- else
- break;
- }
- qiju[i][j][k][1] = cnt;
- }
- }
- }
- void CWuZiQi::ValueTheChessboardNaive( const int points[16][16], int qiju[16][16][8][2], int a1[16][16], int a2[16][16] )
- {
- int i, j, k;
- int win;
- /******************根据评分规则对每一个空格评分***************/
- for ( i = 1; i <= 15; i++ ) // col
- for ( j = 1; j <= 15; j++ ) // row
- {
- if ( points[i][j] == 0 )
- {
- win = 0;
- for ( k = 0; k < 4; k++ ) // direction
- {
- if ( qiju[i][j][k][0] + qiju[i][j][k+4][0] >= 4 )
- win += 10000;
- else if ( qiju[i][j][k][0] + qiju[i][j][k+4][0] == 3 )
- win += 1000;
- else if ( qiju[i][j][k][0] + qiju[i][j][k+4][0] == 2 )
- win += 100;
- else if ( qiju[i][j][k][0] + qiju[i][j][k+4][0] == 1 )
- win += 10;
- }
- a1[i][j] = win; // black
- win = 0;
- for ( k = 0; k < 4; k++ ) // direction
- {
- if ( qiju[i][j][k][1] + qiju[i][j][k+4][1] >= 4 )
- win += 10000;
- else if ( qiju[i][j][k][1] + qiju[i][j][k+4][1] == 3 )
- win += 1000;
- else if ( qiju[i][j][k][1] + qiju[i][j][k+4][1] == 2 )
- win += 100;
- else if ( qiju[i][j][k][1] + qiju[i][j][k+4][1] == 1 )
- win += 10;
- }
- a2[i][j] = win; // white
- }
- }
- }
五子棋AI设计——从门外到门内不得不说的事儿3
第三天——进攻防守,视情况而定
在第二天,AI可以防守了,但是我们设计AI绝对不是为了让AI被动挨打,而是适时地主动出击。那么,是时候回答第二天的遗留问题——什么条件下进攻,什么条件下防守?
第二天,我们提出了阴线评估函数的概念,并且成功的利用阴线评估函数指导AI进行防守。那么是不是需要一个新的什么函数来指导进行呢?好吧,在试图构思这个新函数之前,让我们再看看阴线评估函数。
在阴线评估函数中,我们对每个棋子沿8个方向上的连续出现的一种颜色的棋子进行统计。同时将统计结果记录在qiju中,qiju[i][j][k][s]代表棋盘上(i,j)位置是空位置,那么它沿第k个方向连续出现的黑子数目记录在s=0中,白子数目记录在s=1中。然后分别对s=0和s=1进行统计,得到a1[i][j]和a2[i][j]。
好了,加入人先持黑,AI后手持白。那么,在第二天,AI选择的是a1中数值最大的位置落子,意思就是AI认为这个位置潜在威胁最大!!在这里落子可以降低对手的威胁。现在,设a1的最大值为Max1,对应的坐标为(x1,y1);a2的最大值为Max2,对应的坐标为(x2,y2)。
那么Max2对应的(x2,y2)是不是就是当前对AI最有利的落子位置呢?
就目前的评估函数来说是的。好了,经过简单的回顾阴线评估函数的定义,我们完全没有必要重新定义一个新的评估函数来指导AI进攻,而是充分挖掘一下阴线评估函数,利用Max1和Max2来决策是否进攻就好了。
当Max1>=Max2时,意味着威胁大于优势,AI最好选择防守,否则AI可以选择进攻。落子的位置,如果选择了防守,落子在(x1,y1),否则落子在(x2,y2)。
到目前为止,AI基于我们简陋的阴线评估函数可以自己决定是进攻还是防守,事实证明,基于这个方法,AI的水平算是基本入门了……
我们的AI终于入门了,那么,如何提高AI的决策水平呢?也就是说,仅仅使用阴线评估函数来支撑决策是不够的,我们需要另外一个评估函数来支撑AI决策。这个评估函数将是什么?如何使用,且听下回分解——MinMax算法。
--------------------分割线--------------------
AI的实现代码如下,
- void CWuZiQi::AI_2( const int points[16][16], bool first, int oldp[16][16], int newp[16][16], int *nx, int *ny )
- {
- int i, j;
- int x, y;
- int x1 = 0, x2 = 0, y1 = 0, y2 = 0;
- int qiju[16][16][8][2];
- int a1[16][16], a2[16][16];
- // current state quick save
- for ( i = 1; i <= 15; i++ )
- for ( j = 1; j <= 15; j++ )
- {
- oldp[i][j] = points[i][j];
- newp[i][j] = points[i][j];
- }
- FillMatrix( qiju, 0 );
- FillMatrix( a1, 0 );
- FillMatrix( a2, 0 );
- HowManyInLine( oldp, qiju );
- ValueTheChessboardNaive( oldp, qiju, a1, a2 );
- //PrintMatrix( qiju );
- //PrintMatrix( oldp );
- /****************算出分数最高的空位,填写坐标*********************/
- for( i = 1; i <= 15; i++ )
- for( j = 1; j <= 15; j++ )
- {
- if( a1[x1][y1] < a1[i][j] )
- {x1 = i; y1 = j;} // black
- }
- for( i = 1; i <= 15; i++ )
- for( j = 1; j <= 15; j++ )
- {
- if( a2[x2][y2] < a2[i][j] )
- {x2 = i; y2 = j;} // white
- }
- if ( first )
- {
- if ( a1[x1][y1] > a2[x2][y2] )
- {x = x1; y = y1;}
- else
- {x = x2; y = y2;}
- newp[x][y] = 1;
- }
- else
- {
- if ( a2[x2][y2] > a1[x1][y1] )
- {x = x2; y = y2;}
- else
- {x = x1; y = y1;}
- newp[x][y] = 2;
- }
- *nx = x; *ny = y;
- }
五子棋AI设计——从门外到门内不得不说的事儿4
第四天——看得远胜算更大
经过三天的不断改进,我们的AI算是入门了,如何提高呢——高人指点说,“看得远,胜算才能更大。”道理确实如此,高人所说的“看得远”就是前瞻了,如何前瞻呢?前瞻之后如何决策?
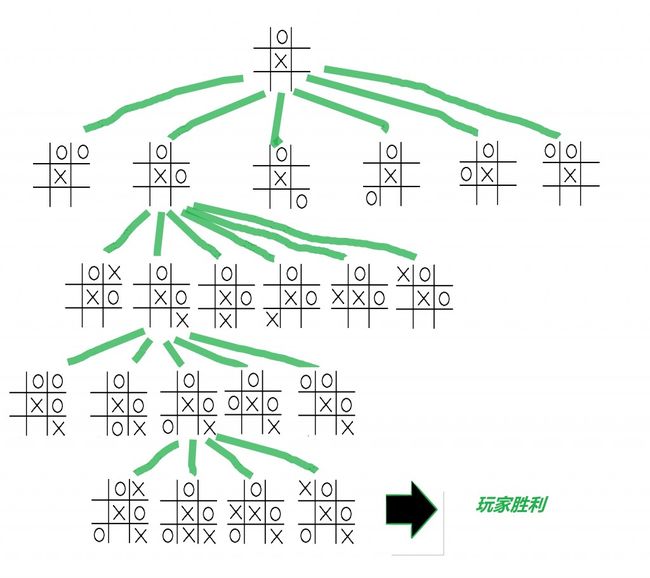
先说说什么是前瞻吧。前瞻就是把所有可能的局面都推算出来,然后给每个局面打个分,从中选出一个最有利于自己的走法来作为当前的走法。但是如何选择呢?为了方便说明问题,我们先以3x3的棋盘为例。以图1来说说吧。为了说起来方便,我们约定如下,根节点表示当前棋局,假设AI先手,持黑,用圆圈表示,玩家后手持白,用叉表示。轮到AI出招。很显然,目前AI可以落子的位置共有7个,图1画了6种情况。我们称这一层的节点分别为q11,q12,...,q17。AI落子后,轮到玩家出招。我们从q12出发,玩家可能的落子对应的棋局分别为q21,q22,q23,...,q26。玩家落子后,轮到AI出招。我们从q22出发,AI可能的落子对应的棋局分别为q31,q32,...,q35。如此推下去,我们可以得到一颗庞大的博弈树,比如从q33出发,得到q41,q42,q43,q44。其中q44代表玩家胜利。为了在当前情况下做出最好的决策,生成完整的博弈树绝对是最好的。可是对于3x3的情况,从图1所示的根节点出发,推出的博弈树就有7!个叶节点,可想对于15x15的情况,这棵树的叶节点对多到我们无法承受的程度。所以,生成完整的博弈树不仅在空间上不可能,在时间上也是不现实的。所以,我们只能前瞻有限步,我们称玩家落子一次,AI再落子一次为一步。那么,图1对应的应该是前瞻两步。
图1 部分博弈树举例
假如,我们生成了完整的博弈树,对于叶节点的打分是很简单的。如果是AI胜利就给1分,如果玩家胜利就给-1分,如果平手就给0分。当前瞻步数有限时,如何评价叶节点就显得很重要,这是其一。其次,如何利用这些给分来决策也很重要。
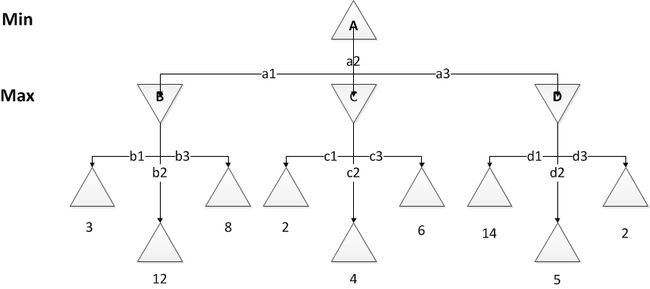
下面说说如何决策。首先我们进一步简化我们所面临的情况,假设我们可以得到一颗完整的博弈树如图2。叶节点下面的数值表示使用评分函数给出的该叶节点的分数。假设A节点轮到AI决策,B、C、D为AI可能的落子。bi、cj、dk分别表示玩家落子后最终的棋局。那么,AI该如何决策呢?在博弈时,双方都想战胜对手,那么可以假设双方是完全理性的。那么,在AI落子后,假设对应棋局B,那么玩家可能的落子对应三个终局b1、b2和b3,那么玩家决策时使用的评分函数是分析对自己的好处或者是对AI的威胁,那么分数表示对自己有利或者对AI不利的程度,那么玩家会选择对自己最好的b2。依此类推,可以知道在B、C、D节点玩家的最优选择是b2、c3和d1。那么此时AI的选择是尽量降低玩家对自己造成的的不利而选择其中的最小值即c3。如果,我们将评分函数定义为对AI的有利程度,那么,玩家肯定会选择最小值,即b1、c1和d3,而AI会选择其中的最大值b1。极大极小的选择取决于评分函数的定义。按照第一种定义,AI会偏保守,按照第二种定义,AI会偏向进攻。
图2 简化的完整博弈树
但是无论如何,上面的分析过程给出了我们一个关于如何决策的提示。这个决策基于两个假设:1、博弈双方完全理性;2、信息完全可知。基于这两个假设,在知道轮到谁出招和评分函数的具体定义后,我们按照极小、极大交替选择,最终确定一个选择支撑棋手决策。假设,我们约定AI的设计偏保守,对于叶节点的评价函数定义为对玩家的有利程度或对AI的威胁程度。并且前瞻步数为k,当前轮到AI出招。定义玩家为极大棋手,AI为极小棋手。从根节点开始包括根节点,依次为Min层、Max层,依此类推交替到叶节点。但是,前面说到了,完全理性即有能力生成整个博弈树在实际对弈中是不能实现的,所以完全理性假设是不成立的。部分理性是可以实现的,即在有限步内按照极大极小交替决策。
现在的关键问题是,如何对叶节点进行打分,也就是我们看到的那些数值应该怎么给出将决定极小极大决策的结果的好坏。其次,仅仅是有限步的博弈树也是很大的,如何有效地在博弈树上进行搜索也是一个亟待解决的问题。
如何评价非终局的棋局按住暂且不表,先说说如何提高搜索,且听下回分解——alpha-beta剪枝。
五子棋AI设计——从门外到门内不得不说的事儿5
第五天——可以看得更远,可以思考的更快
看得远,胜算更大;看得远,产生的棋局越多,需要判断的状态就越多,AI的思考时间就越长。从游戏性角度出发,我们不仅希望AI能够胜利,更希望它的思考时间在可以容忍的范围内。
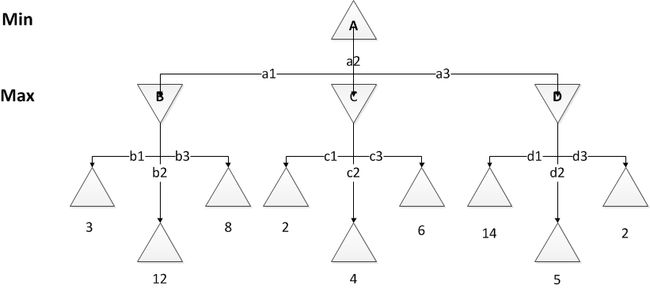
图1 前瞻1步的博弈树
现在的问题是——如何在数量无比庞大的状态中快速的找到最优的走子策略。在博弈搜索中,博弈树叶节点的值为当前状态的得分。如图1所示博弈树中,B节点的值为12,此时A节点的值应该小于等于12。C节点的值为6,小于12,那么A节点的值此时应该小于等于6。计算D节点时,d1节点的值为14,可以推知D节点的值大于等于14与A节点的值小于等于6矛盾,因此将D节点余下的子节点剪去。这就是alpha-beta剪枝。伪代码如下:
- function MinMax-Decision(state) returns an action
- inputs: state, current state in game
- v←Min-Value(state, -∞, +∞, k)
- return the action in Successors(state) with value v
- function Max-Value(state, α, β, k) return a utility vale
- inputs: state, current state in game
- α, the value of the best alternative for Max along the path to state
- β, the value of the best alternative for Min along the path to state
- k, current depth in game path
- if k == 0 then return UTILITY(state)
- v←-∞
- for s in Successors(state) do
- v←MAX(v, Min-Value(s, α, β, k-1))
- if v≥β then return v
- α←MAX(α, v)
- return v
- function Min-Value(state, α, β, k) return a utility vale
- inputs: state, current state in game
- α, the value of the best alternative for Max along the path to state
- β, the value of the best alternative for Min along the path to state
- k, current depth in game path
- if k == 0 then return UTILITY(state)
- v←+∞
- for s in Successors(state) do
- v←MIN(v, Max-Value(s, α, β, k-1))
- if v≤α then return v
- β←MIN(β, v)
- return v
当前瞻d步、每步的合法走子有n种时,剪枝前的时间复杂度为O(n^d),剪枝后为 O(n^(d/2))。在相同时间内,剪枝后前瞻的步数是原来的两倍;在相同的步数内,搜索到结果的时间是原来的平方根。刚好符合我们的需求。
现在,我们明确了前瞻步数和AI思考时间之间的关系,就可以根据AI的等级确定前瞻步数,同时约束思考时间。在讨论了如何搜索和如何提高搜索效率后,下面我们将集中讨论如何设计评估器,也就是博弈树中每个叶节点的数值是如何确定的。
--------------------分割线--------------------
- void CWuZiQi::MaxMinDecision( const int points[16][16], bool first, int oldp[16][16], int newp[16][16], int *nx, int *ny, int k )
- {
- int i, j, t;
- int x, y;
- int cntr;
- MyPoint v[KMAX];
- int numbq, numwq;
- int a1[16][16], a2[16][16];
- //int tiju[16][16][8][2];
- MyPoint b[225], w[225];
- //out = fopen( "mm.txt", "w" );
- for ( i = 1; i <= 15; i++ )
- for ( j = 1; j <= 15; j++ )
- {
- oldp[i][j] = points[i][j];
- newp[i][j] = points[i][j];
- }
- for ( i = 0; i < KMAX; i++ )
- {v[i].val = 0; v[i].x = 0; v[i].y = 0;}
- cntr = QuickCount( oldp );
- if ( cntr == 1 )
- {
- *nx = 7; *ny = 7;
- newp[7][7] = 2;
- return;
- }
- MinValue( oldp, first, -MAX, MAX, k, v );
- //
- /*
- FillMatrix( tiju, 0 );
- HowManyInLine( oldp, tiju );
- ValueTheChessboardNaive( oldp, tiju, a1, a2 );
- */
- FillMatrix( a1, 0 );
- FillMatrix( a2, 0 );
- MaxMinValuationOnEmpty( oldp, a1, a2 );
- FillMatrix( b, a1 );
- FillMatrix( w, a2 );
- SortTheValuation( b, w, &numbq, &numwq );
- PrintMatrix( b, w, numbq, numwq );
- //
- int cur = b[0].val - w[0].val;
- int fur = v[k - 1].val;
- if ( first )
- {
- if ( cur < 0 && fur > 0 ) // both current and future are dangerous
- {
- if ( cur + fur <= 0 )
- {x = w[0].x; y = w[0].y;} // current is worse
- else // future is better, but it isn't sure
- {
- t = rand() % 1000;
- if ( t < 100 )
- {x = v[k - 1].x; y = v[k - 1].y;} // future
- else
- {x = w[0].x; y = w[0].y;} // current
- }
- }
- else if ( cur >= 0 && fur <= 0 ) // both current and future are ok
- {
- if ( cur + fur > 0 ) // current is better
- {x = b[0].x; y = b[0].y;}
- else // future is better, but it isn't sure
- {
- t = rand() % 1000;
- if ( t < 200 )
- {x = v[k - 1].x; y = v[k - 1].y;} // defence
- else
- {x = b[0].x; y = b[0].y;} // attack
- }
- }
- else if ( cur < 0 && fur <= 0 ) //current is bad, further is ok
- {
- if ( cur < fur ) // current is more dangerous than future
- {x = w[0].x; y = w[0].y;}
- else // future is better, but it isn't sure
- {
- t = rand() % 1000;
- if ( t < 100 )
- {x = v[k - 1].x; y = v[k - 1].y;} // future
- else
- {x = w[0].x; y = w[0].y;} // current
- }
- }
- else //current is ok, further is bad
- {
- if ( cur > fur ) // current is better
- {x = b[0].x; y = b[0].y;}
- else // future is worse, but current is not that bad
- {
- t = rand() % 1000;
- if ( t < 400 )
- {x = v[k - 1].x; y = v[k - 1].y;} // defence
- else
- {x = b[0].x; y = b[0].y;} // attack
- }
- }
- newp[x][y] = 1;
- }
- else
- {
- if ( cur >= 0 && fur >= 0 ) // both current and future are dangerous
- {
- if ( cur > fur )
- {x = b[0].x; y = b[0].y;} // current is worse
- else // future is better, but it isn't sure
- {
- t = rand() % 1000;
- if ( t < 100 )
- {x = v[k - 1].x; y = v[k - 1].y;} // future
- else
- {x = b[0].x; y = b[0].y;} // current
- }
- }
- else if ( cur < 0 && fur < 0 ) // both current and future are ok
- {
- if ( cur < fur ) // current is better
- {x = w[0].x; y = w[0].y;}
- else // future is better, but it isn't sure
- {
- t = rand() % 1000;
- if ( t < 200 )
- {x = v[k - 1].x; y = v[k - 1].y;} // defence
- else
- {x = w[0].x; y = w[0].y;} // attack
- }
- }
- else if ( cur >= 0 && fur < 0 ) //current is bad, further is ok
- {
- if ( cur + fur > 0 ) // current is more dangerous than future
- {x = b[0].x; y = b[0].y;}
- else // future is better, but it isn't sure
- {
- t = rand() % 1000;
- if ( t < 100 )
- {x = v[k - 1].x; y = v[k - 1].y;} // future
- else
- {x = b[0].x; y = b[0].y;} // current
- }
- }
- else //current is ok, further is bad
- {
- if ( cur + fur < 0 ) // current is better
- {x = w[0].x; y = w[0].y;}
- else // future is worse, but current is not that bad
- {
- t = rand() % 1000;
- if ( t < 400 )
- {x = v[k - 1].x; y = v[k - 1].y;} // defence
- else
- {x = w[0].x; y = w[0].y;} // attack
- }
- }
- newp[x][y] = 2;
- }
- //fclose( out );
- *nx = x; *ny = y;
- }
- void CWuZiQi::MaxValue( const int qp[16][16], bool first, int alpha, int beta, int k, MyPoint res[KMAX] )
- {
- int i, j, val;
- int tqp[16][16], t[16][16];
- MyPoint v;
- //
- FillMatrix( t, 0 );
- for ( i = 1; i <= 15; i++ )
- for ( j = 1; j <= 15; j++ )
- t[i][j] = qp[i][j];
- //
- if ( k == 0 )
- {
- //PrintMatrix( qp );
- val = MaxMinValuationOnNonempty( t, first );
- res[k].val = val;
- //fprintf( out, "%d\t%d\t%d\t%d------(%d, %d)MAX0\n", k, res[k].x, res[k].y, res[k].val, alpha, beta );
- return;
- }
- v.val = -MAX;
- for ( i = 1; i <= 15; i++ )
- for ( j = 1; j <= 15; j++ )
- {
- if ( qp[i][j] != 0 )
- continue;
- FillMatrix( tqp, 0 );
- FillMatrix( tqp, t );
- if ( first )
- tqp[i][j] = 2;
- else
- tqp[i][j] = 1;
- res[k - 1].x = i; res[k - 1].y = j;
- MinValue( tqp, first, alpha, beta, k - 1, res );
- if ( v.val < res[k - 1].val )
- {v.val = res[k - 1].val; v.x = res[k - 1].x; v.y = res[k - 1].y;}
- if ( v.val >= beta )
- {
- res[k - 1].val = v.val; res[k - 1].x = v.x; res[k - 1].y = v.y;
- //fprintf( out, "%d\t%d\t%d\t%d------(%d, %d)MAX1\n", k, v.x, v.y, v.val, alpha, beta );
- return;
- }
- if ( v.val > alpha )
- {
- alpha = v.val;
- //fprintf( out, "%d\t%d\t%d\t%d------(%d, %d)MAX2\n", k, v.x, v.y, v.val, alpha, beta );
- }
- }
- if ( k == KMAX )
- {res[k - 1].val = v.val; res[k - 1].x = v.x; res[k - 1].y = v.y;}
- else
- {res[k].val = v.val; res[k].x = v.x; res[k].y = v.y;}
- //fprintf( out, "%d\t%d\t%d\t%d------(%d, %d)MAX3\n", k, v.x, v.y, v.val, alpha, beta );
- }
- void CWuZiQi::MinValue( const int qp[16][16], bool first, int alpha, int beta, int k, MyPoint res[KMAX] )
- {
- int i, j, val;
- int tqp[16][16], t[16][16];
- MyPoint v;
- //
- FillMatrix( t, 0 );
- for ( i = 1; i <= 15; i++ )
- for ( j = 1; j <= 15; j++ )
- t[i][j] = qp[i][j];
- //
- if ( k == 0 )
- {
- //PrintMatrix( qp );
- val = MaxMinValuationOnNonempty( t, first );
- res[k].val = val;
- //fprintf( out, "%d\t%d\t%d\t%d------(%d, %d)MIN0\n", k, res[k].x, res[k].y, res[k].val, alpha, beta );
- return;
- }
- v.val = MAX;
- for ( i = 1; i <= 15; i++ )
- for ( j = 1; j <= 15; j++ )
- {
- if ( t[i][j] != 0 )
- continue;
- FillMatrix( tqp, 0 );
- FillMatrix( tqp, t );
- if ( first )
- tqp[i][j] = 1;
- else
- tqp[i][j] = 2;
- res[k - 1].x = i; res[k - 1].y = j;
- MaxValue( tqp, first, alpha, beta, k - 1, res );
- if ( v.val > res[k - 1].val )
- {v.val = res[k - 1].val; v.x = res[k - 1].x; v.y = res[k - 1].y;}
- if ( v.val <= alpha )
- {
- res[k - 1].val = v.val; res[k - 1].x = v.x; res[k - 1].y = v.y;
- //fprintf( out, "%d\t%d\t%d\t%d------(%d, %d)MIN1\n", k, v.x, v.y, v.val, alpha, beta );
- return;
- }
- if ( v.val < beta )
- {
- beta = v.val;
- //fprintf( out, "%d\t%d\t%d\t%d------(%d, %d)MIN2\n", k, v.x, v.y, v.val, alpha, beta );
- }
- }
- if ( k == KMAX )
- {res[k - 1].val = v.val; res[k - 1].x = v.x; res[k - 1].y = v.y;}
- else
- {res[k].val = v.val; res[k].x = v.x; res[k].y = v.y;}
- //fprintf( out, "%d\t%d\t%d\t%d------(%d, %d)MIN3\n", k, v.x, v.y, v.val, alpha, beta );
- }
五子棋AI设计——从门外到门内不得不说的事儿6
第6天——评价的准才能胜券在握
在博弈类游戏中,都可以使用博弈搜索求解最优解,但是最优解的质量如何取决于评估器的质量,也就是说AI对棋局态势的感知能力。
在不考虑时间时,我们可以让AI前瞻若干步直到终局,终局评估器设计起来就很简单,AI胜利给个正1,AI败北给个负1,平局给个0。完全博弈树的叶节点的数量很大,因此产生终局的时间代价是不能容忍的,我们只能让AI前瞻有限步。如何对中间局进行评价,可以理解成AI对于中间局的感知能力。
之前我们介绍了阳线评估器和阴线评估器,并说明了每个评估器的应用场合。对于阳线评估器的设计相对简单,只要讨论几种模式就可以了,每种模式和对应的得分见表1。
| 模式 |
五连 |
四连 |
双三连 |
三连 |
双二连 |
二连 |
一连 |
| 分数 |
100000 |
25000 |
15000 |
10000 |
250 |
100 |
10 |
表1 阳线模式评分表
阴线评估器的设计相对复杂一些,不仅要考虑一个方向还有考虑两个方向,模式及得分见表2、3。
| 模式 |
评分 |
| 四连 |
100000 |
| 三连两端为空 |
100000 |
| 三连两端非空 |
10000 |
| 二连 |
10 |
| 一连 |
1 |
表2 阴线一个方向的模式评分表
| 相隔45、90 135度 |
相隔180度 |
||
| 模式 |
评分 |
模式 |
评分 |
| 双四连 |
100000 |
>=4 |
100000 |
| 双三连一端为空 |
100000 |
=3两端空 |
100000 |
| 三连和二连一端为空 |
10000 |
=3两端非空 |
1 |
| 三连和二连一端非空 |
100 |
=3一端空 |
10 |
| 三连和一连 |
10 |
=2两端空 |
10000 |
| 双二连两端空 |
100000 |
=2两端非空 |
1 |
| 双二连一端空 |
10000 |
=2一端空 |
10 |
| 双二连两端非空 |
100 |
- |
- |
| 二连一连一端空 |
10000 |
- |
- |
| 其他 |
- |
- |
- |
表3 阴线两个方向的模式评分表
表1、2和3的模式仅仅是我能够想到的模式中的一部分,能够简单表示的一部分模式,还有很多其他的模式。因此,另外一种设计评估器的方法就是记棋谱。说到这里,我们不难发现,AI的最高水平要略低于开发者玩该游戏的水平,因此我设计的AI目前仅仅能算是个初学者。同时,每种模式的给分情况也是我根据自己的感觉随便给的,如何设计每种模式的得分又是一个问题。在阅读别人的论文时,主流的评分方法是使用神经网络进行训练,然后利用训练的网络作为评估器每种模式的得分。
讨论了半天,我们还是在原地打转,最最根本的问题并没有得到解决。按照这种技术路线继续走下去,我们设计的AI的水平最好能够达到我们自己的水平,而不能够更高。细细想想,其实min-max搜索,加上alpha-beta剪枝并不是AI的关键,关键是评估器的设计,而评估器的设计实质上是将人的经验形式化转换成计算机的数据结构或者代码。如何让计算机自己学习这一过程,也许才是人工智能的发展方向,目前这种方法充其量还是在模拟人的智能模式。如果能够创造出一种新的智能模式,那么我们又何必挖空心思复现人的智能模式呢,就像地外生命形式一样。如果存在非碳基的生命形式,我们就不会显得如此狭隘,如此孤独,如此自大。如果智能能够被界定成生命的话,那么非人类模式的智能会是什么样,硅基智能吗,计算智能吗,路漫漫啊。
--------------------分割线--------------------
- int CWuZiQi::MaxMinValuationOnNonempty( const int oldp[16][16], bool first )
- {
- int i, j, k, t, s, cnt;
- int tx, ty;
- int dx[4] = {1, 1, 0, -1};
- int dy[4] = {0, 1, 1, 1};
- int tiju[16][16][8][2];
- int mark[16][16][8][2];
- int res = 0;
- int typeq[8][2] = {0};
- int type[8] = {0};
- int score[8] = {100000, 25000, 15000, 10000, 250, 100, 10, 1};
- //count
- FillMatrix( tiju, 0 );
- FillMatrix( mark, 0 );
- /****************为双方填写棋型表************/
- for ( i = 1; i <= 15; i++ ) // col
- {
- for ( j = 1; j <= 15; j++ ) // row
- {
- if ( oldp[i][j] != 0 )
- {
- for ( k = 0; k < 4; k++ ) // direction
- {
- if ( oldp[i][j] == 1 )
- {
- if ( mark[i][j][k][0] == 0 )
- {
- cnt = 1;
- tx = i;
- ty = j;
- mark[tx][ty][k][0] = 1;
- for ( t = 0; t < 5; t++ )
- {
- tx += dx[k];
- ty += dy[k];
- if ( tx > 15 || tx < 1 || ty > 15 || ty < 1 )
- break;
- if( oldp[tx][ty] == 1 )
- {
- cnt++;
- mark[tx][ty][k][0] = 1;
- }
- else
- break;
- }
- tiju[i][j][k][0] = cnt;
- if ( cnt == 5 )
- typeq[0][0]++;
- else if ( cnt == 4 )
- typeq[1][0]++;
- else if ( cnt == 3 )
- typeq[3][0]++;
- else if ( cnt == 2 )
- typeq[5][0]++;
- else if ( cnt == 1 )
- {
- typeq[6][0]++;
- for ( int ii = 0; ii < 4; ii++ )
- mark[i][j][ii][0] = 1;
- }
- }
- }
- else if ( oldp[i][j] == 2 )
- {
- if ( mark[i][j][k][1] == 0 )
- {
- cnt = 1;
- tx = i;
- ty = j;
- mark[tx][ty][k][1] = 1;
- for ( t = 0; t < 5; t++ )
- {
- tx += dx[k];
- ty += dy[k];
- if ( tx > 15 || tx < 1 || ty > 15 || ty < 1 )
- break;
- if( oldp[tx][ty] == 2 )
- {
- cnt++;
- mark[tx][ty][k][1] = 1;
- }
- else
- break;
- }
- tiju[i][j][k][1] = cnt;
- if ( cnt == 5 )
- typeq[0][1]++;
- else if ( cnt == 4 )
- typeq[1][1]++;
- else if ( cnt == 3 )
- typeq[3][1]++;
- else if ( cnt == 2 )
- typeq[5][1]++;
- else if ( cnt == 1 )
- {
- typeq[6][1]++;
- for ( int ii = 0; ii < 4; ii++ )
- mark[i][j][ii][1] = 1;
- }
- }
- }
- }
- for ( s = 0; s < 2; s++ )
- {
- t = 0;
- for ( k = 0; k < 4; k++ )
- if ( tiju[i][j][k][s] == 3 )
- t++;
- if ( t == 2 )
- typeq[2][s] += 1;
- else if ( t == 3 )
- typeq[2][s] += 3;
- else if ( t == 4 )
- typeq[2][s] += 6;
- t = 0;
- for ( k = 0; k < 4; k++ )
- if ( tiju[i][j][k][s] == 2 )
- t++;
- if ( t == 2 )
- typeq[4][s] += 1;
- else if ( t == 3 )
- typeq[4][s] += 3;
- else if ( t == 4 )
- typeq[4][s] += 6;
- }
- }
- }
- }
- //PrintMatrix( tiju );
- //PrintMatrix( oldp );
- //value
- for ( i = 0; i < 7; i++ )
- {
- if ( first )
- type[i] = typeq[i][0] - typeq[i][1];
- else
- type[i] = typeq[i][0] - typeq[i][1];
- res += type[i] * score[i];
- }
- //
- if ( first )
- return -res;
- else
- return res;
- }
- void CWuZiQi::MaxMinValuationOnEmpty( const int oldp[16][16], int a1[16][16], int a2[16][16] )
- {
- int i, j, k, t, s, cnt, ii, jj;
- int tx, ty;
- int barrier;
- int win[2];
- int dx[8] = {0, 1, 1, 1, 0, -1, -1, -1};
- int dy[8] = {-1, -1, 0, 1, 1, 1, 0, -1};
- int type[8][2];
- int p[16][16];
- for ( i = 0; i < 16; i++ )
- for ( j = 0; j < 16; j ++ )
- p[i][j] = oldp[i][j];
- //couny
- /****************为双方填写棋型表************/
- for ( i = 1; i <= 15; i++ ) // col
- {
- for ( j = 1; j <= 15; j++ ) // row
- {
- if ( oldp[i][j] == 0 )
- {
- for ( ii = 0; ii < 8; ii++ )
- for ( jj = 0; jj < 2; jj++ )
- type[ii][jj] = 0;
- // count
- for ( k = 0; k < 8; k++ ) // direction
- {
- //
- cnt = 0; tx = i; ty = j; barrier = 0;
- for ( t = 0; t < 5; t++ )
- {
- tx += dx[k]; ty += dy[k];
- if ( tx > 15 || tx < 1 || ty > 15 || ty < 1 ) {barrier = 1; break;}
- if( oldp[tx][ty] == 1 ) cnt++;
- else
- {
- if ( oldp[tx][ty] == 2 ) barrier = 1;
- break;
- }
- }
- type[k][0] = cnt * 2 + barrier;
- //
- cnt = 0; tx = i; ty = j; barrier = 0;
- for ( t = 0; t < 5; t++ )
- {
- tx += dx[k]; ty += dy[k];
- if ( tx > 15 || tx < 1 || ty > 15 || ty < 1 ) {barrier = 1; break;}
- if( oldp[tx][ty] == 2 ) cnt++;
- else
- {
- if ( oldp[tx][ty] == 1 ) barrier = 1;
- break;
- }
- }
- type[k][1] = cnt * 2 + barrier;
- }
- // value
- for ( t = 0; t < 2; t++ )
- {
- win[t] = 0;
- for ( k = 0; k < 8; k++ ) // single line
- {
- int t1, s1;
- if ( type[k][t] % 2 == 0 ) {t1 = type[k][t] / 2; s1 = 0;}
- else {t1 = ( type[k][t] - 1 ) / 2; s1 = 1;}
- if ( t1 >= 4 )
- win[t] += 100000;
- else if ( t1 == 3 && s1 == 0 )
- win[t] += 100000;
- else if ( t1 == 3 && s1 == 1 )
- win[t] += 10000;
- else if ( t1 == 2 )
- win[t] += 10;
- else
- win[t] += 1;
- }
- for ( k = 0; k < 8; k++ ) // two line combination, 45 degree, 90 degree and 135 degree
- for ( s = 1; s <= 3; s++ )
- {
- int t1, t2, s1, s2;
- if ( type[k][t] % 2 == 0 ) {t1 = type[k][t] / 2; s1 = 0;}
- else {t1 = ( type[k][t] - 1 ) / 2; s1 = 1;}
- if ( type[( k + s ) % 8][0] % 2 == 0 ) {t2 = type[( k + s ) % 8][t] / 2; s2 = 0;}
- else {t2 = ( type[( k + s ) % 8][t] - 1 ) / 2; s2 = 1;}
- int tmp = t1 + t2;
- //
- if ( t1 == 0 || t2 == 0 )
- continue;
- if ( t1 >= 4 || t2 >= 4 ) {win[t] += 100000; continue;}
- else if ( t1 == 3 || t2 == 3 )
- {
- if (( t1 == 3 && s1 == 0 ) || ( t2 == 3 && s2 == 0 )) {win[t] += 100000; continue;}
- else if (( t1 == 2 && s1 == 0 ) || ( t2 == 2 && s2 == 0 )) {win[t] += 10000; continue;}
- else if (( t1 == 2 && s1 == 1 ) || ( t2 == 2 && s2 == 1 )) {win[t] += 100; continue;}
- else if (( t1 == 1 ) || ( t2 == 1 )) {win[t] += 10; continue;}
- else if (( t1 == 0 ) || ( t2 == 0 )) {win[t] += 1; continue;}
- }
- else if ( t1 == 2 || t2 == 2 )
- {
- if (( t1 == 2 && s1 == 0 ) && ( t2 == 2 && s2 == 0 )) {win[t] += 100000; continue;}
- else if (( t1 == 2 && s1 == 1 ) && ( t2 == 2 && s2 == 1 )) {win[t] += 100; continue;}
- else if (( t1 == 2 && s1 == 1 ) && ( t2 == 2 && s2 == 0 ) || ( t1 == 2 && s1 == 0 ) && ( t2 == 2 && s2 == 1 ))
- {win[t] += 10000; continue;}
- if (( t1 == 2 && s1 == 0 ) || ( t2 == 2 && s2 == 0 )) {win[t] += 10000; continue;}
- else {win[t] += 100; continue;}
- }
- else if ( t1 == 1 || t2 == 1 )
- {win[t] += 1; continue;}
- }
- for ( k = 0; k < 4; k++ ) // two line combination 180 degree
- {
- int t1, t2, s1, s2;
- if ( type[k][t] % 2 == 0 ) {t1 = type[k][t] / 2; s1 = 0;}
- else {t1 = ( type[k][t] - 1 ) / 2; s1 = 1;}
- if ( type[( k + 4 ) % 8][0] % 2 == 0 ) {t2 = type[( k + 4 ) % 8][t] / 2; s2 = 0;}
- else {t2 = ( type[( k + s ) % 8][t] - 1 ) / 2; s2 = 1;}
- int tmp = t1 + t2;
- //
- if ( t1 == 0 || t2 == 0 )
- continue;
- if ( tmp >= 4 )
- {win[t] += 100000;continue;}
- else if ( tmp == 3 )
- {
- if ( s1 == 0 && s2 == 0 ) {win[t] += 100000;continue;}
- else if ( s1 == 1 && s2 == 1 ) {win[t] += 1;continue;}
- else {win[t] += 10;continue;}
- }
- else if ( tmp == 2 )
- {
- if ( s1 == 0 && s2 == 0 ) {win[t] += 10000;continue;}
- else if ( s1 == 1 && s2 == 1 ) {win[t] += 1;continue;}
- else {win[t] += 10;continue;}
- }
- }
- }
- a1[i][j] = win[0];
- a2[i][j] = win[1];
- }
- }
- }
- }
第7天——结
7作为一个神奇的数字,许许多多具有特殊意义的事情往往会发生在第7日。作为一个小连载,课程内的五子棋系列就在这里作结吧。
从门外到门里,虽然只有一步之遥,但是我们还是走了好几天。简单回顾一下我们的历程:
第一天:Naive AI——一个称不上AI的AI
第二天:防守,堵堵堵(阴线评估器)
第三天:进攻防守,视情况而定(利用阴线评估器的信息来决策)
第四天:看得远胜算更大(MinMax)
第五天:可以看得更远,可以思考的更快(alpha-beta剪枝)
第六天:评价的准才能胜券在握(评估器设计,再谈阴线评估器)
仔细一看,我们大部分时间都在讨论评估器,而且在第六天悲剧的发现我们走的技术路线不对路,所设计的AI不会比自己聪明,绕来绕去只是在原地转了转。现实往往如此,有时候能够证伪也是一个很大的成功,至少后来人可以少走弯路,或者有经验可循。
那么,博弈类的AI到底该如何设计,可能涉及到很深的理论问题,诸如我们是不是能够完全复现人的脑功能之类的问题等。还有许多工程技术问题,诸如这么个人工脑如何实现,如何连线等。虽然人工智能的未来还不是一片坦途,但是正因为如此它才显得异常迷人,让无数人为之轻狂,无法自拔。在这里我不想讨论有关人工智能的伦理问题,我只想有一天我们可以从简单、机械、重复的工作中解脱出来,真真正正的去发现存在的价值,而不是忙忙碌碌的一生活不明白为了什么。那么,从这个角度考虑,研究人工智能是解决这个问题的必由之路。
也许这一路上满布荆棘,但是谁又会拒绝狂风暴雨之后的彩虹呢,踏上征程,大步奔向美好的明天。
后记:
作为课内作业,设计博弈类游戏堪称是理解人工智能的典范,就像变速箱设计之于机械设计。整个设计过程涵盖了太多的细节,太多的值得思考的知识点。实践证明,任何问题,别人解决了,你可以在不借助帮助的情况下自己实现,只是会消耗很多时间,会牵扯很多精力,可是做学问搞技术,必须要能静得下了,能耐住的寂寞。不自己实实在在的写写,亲手动动,很难真正理解。
用这句诗与诸君共勉——“纸上得来终觉浅,绝知此事要躬行。”