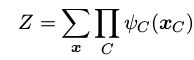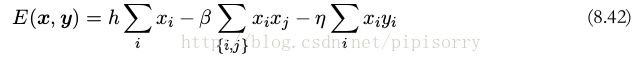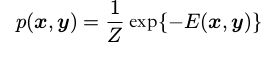马尔可夫随机场 MRF
http://blog.csdn.net/pipisorry/article/details/78396503
马尔可夫网
马尔科夫网是使用无向图描述的图模型,是刻画X上联合分布的一种方法,表示一个分解方式,也表示一组条件独立关系。马尔科夫随机场( Markov random field , MRF),也被称为马尔科夫网络( Markov network )或者无向图模型( undirected graphical model )( Kindermann and Snell, 1980 ),包含一组结点,每个结点都对应着一个变量或一组变量。链接是无向的,即不含有箭头。
与贝叶斯网一样,马尔可夫网可以视为定义了一系列由图结构确定的独立性假设。
条件独立性质
定义一种概率分布的图语义表示,使得条件独立性由单一的图划分确定。
假设在一个无向图中,我们有三个结点集合,记作 A, B, C 。我们考虑条件独立性质
为了判定由图定义的概率分布是否满足这个性质,我们考虑连接集合 A 的结点和集合 B 的结点的所有可能路径。如果所有这些路径都通过了集合 C 中的一个或多个结点,那么所有这样的路径都被“阻隔”,因此条件独立性质成立。
条件独立性包含三种:成对、局部、全局马尔可夫性。
成对马尔可夫性(最大团的由来):
设u和v是无向图G中任意两个没有边连接的节点,节点u和v分别对应随机变量Yu和Yv。其他所有节点为O,对应的随机变量是Yo。成对马尔可夫性是指给定随机变量组Yo的条件下随机变量Yu和Yv是条件独立的,即
P(Yu,Yv|Yo) = P(Yu|Yo)P(Yv|Yo)
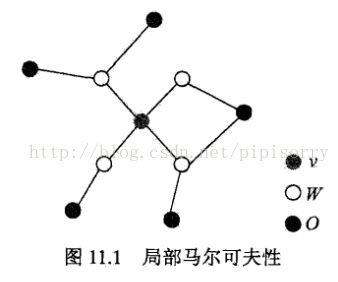
局部马尔可夫性(马尔科夫毯):设v∈V是无向图G中任意一个节点,W是与v有边连接的所有节点,O是v、W以外的其他所有节点。v表示随机变量是Yv,W表示的随机变量组是YW,O表示的随机变量组是Yo。局部马尔可夫性是指在给定随机变量组YW的条件下随机变量Yv与随机变量组Yo是独立的,即
P(Yu,Yv|Yw) = P(Yv|Yw)P(Yo|Yw)
在 P(Yo|YW)> 0时,等价地, P(Yv|Yw)= P(Yv|Yw, Yo)
马尔科夫毯:对于一个无向图,结点 x i 的马尔科夫毯由相邻结点的集合组成。它的性质为:以图中所有剩余变量为条件, x i 的条件概率分布只依赖于马尔科夫毯中的变量。即结点只条件依赖于相邻结点,而条件独立于任何其他的结点。
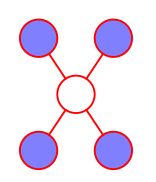
全局马尔可夫性:设节点集合A,B是在无向图G中被节点集合C分开的任意节点集合,如下图所示:
节点集合A,B和C所对应的随机变量组分别是YA,YB,YC。全局马尔可夫性是指给定随机变量组YC条件下随机变量组YA和YB是条件独立的,即
P(YA,YB| YC) = P(YA|YC)P(YB|YC)
无向图的分解
我们更关心如何求其联合概率分布。于是,为了求解给定的概率无向图模型,我们希望将整体的联合概率写成若干个子联合概率的乘积形式,也就是将概率进行因子分解,这样便于模型的学习与计算。而事实上,概率无向图模型的最大特点就是便于因子分解。
如果我们考虑两个结点 x i 和 x j ,它们不存在链接,那么给定图中的所有其他结点,这两个结点一定是条件独立的。
于是,联合概率分布的分解一定要让 x i 和 x j 不出现在同一个因子中,从而让属于这个图的所有可能的概率分布都满足条件独立性质。(lz: 成对马尔科夫性)
团Clique和因子
团( clique ):定义为图中结点的一个子集,使得在这个子集中的每对结点之间都存在链接。换句话说,团块中的结点集合是全连接的。
最大团( maximal clique ):是具有下面性质的团块:不可能将图中的任何一个其他的结点包含到这个团块中而不破坏团块的性质。
图中有五个具有两个结点的团块,即 {x 1 , x 2 }, {x 2 , x 3 }, {x 3 , x 4 }, {x 4 , x 2 } 和 {x 1 , x 3 } ,还有两个最大团块 {x 1 , x 2 , x 3 } 和 {x 2 , x 3 , x 4 } 。集合 {x 1 , x 2 , x 3 , x 4 } 不是一个团块,因为在 x 1 和 x 4 没有链接。
因子:定义为团块中变量的函数。事实上,我们可以 考 虑 最 大 团 块 的 函 数 而 不 失 一 般 性, 因 为 其 他 团 块 一 定 是 最 大 团 块 的 子 集。 因 此, 如果 {x 1 , x 2 , x 3 } 是一个最大团块,并我们在这个团块上定义了任意一个函数,那么定义在这些变量的一个子集上的其他因子都是冗余的。
Hammersley-Clifford定理
概率无向图模型的联合概率分布P(Y)可以表示为如下形式:
其中,C是无向图的最大团,YC是C的节点对应的随机变量,ΨC(YC)是C上定义的严格正函数,乘积是在无向图所有的最大团上进行的。
说明:
让我们将团块记作 C ,将团块中的变量的集合记作 x C 。这样,联合概率分布可以写成图的最大团块的势函数( potential function ) ψ C (x C ) 的乘积的形式。通过只考虑满足 ψ C (x C ) ≥ 0 的势函数,我们确保了 p(x) ≥ 0 。
这里, Z 有时被称为划分函数( partition function ),是一个归一化常数,等于
由于我们的势函数被限制为严格大于零,因此将势函数表示为指数的形式更方便,即
其中 E(x C ) 被称为能量函数( energy function ),指数表示被称为玻尔兹曼分布( Boltzmann distribution )。联合概率分布被定义为势函数的乘积,因此总的能量可以通过将每个最大团块的能量相加的方法得到。(lz Πexp = exp(Σ))
如何选择势函数?可以这样做:将势函数看成一种度量,它表示了局部变量的哪种配置优于其他的配置。具有相对高概率的全局配置对于各个团块的势函数的影响进行了很好的平衡。我们现在通过一个具体的例子来说明无向图的用处。
某小皮
马尔可夫网(条件随机场)在计算机视觉中的应用
图像去噪、去模糊、三维重建、物体识别。
物体识别(图像分割)
[概率图模型]
图像去噪
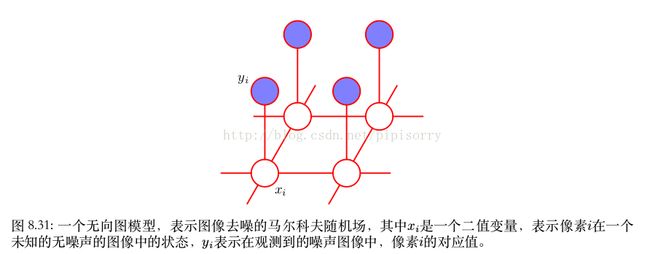
令观测的噪声图像通过一个二值像素值 y i ∈ {−1, +1} 组成的数组来描述,其中下标 i = 1, . . . , D 覆盖了所有的像素。我们假设图像通过下面的方式获得:取一张未知的无噪声图像,这幅图像由二值像素值 x i ∈ {−1, +1} 描述,然后以一个较小的概率随机翻转像素值的符号。由于噪声等级比较小,因此我们知道 x i 和 y i 之间有着强烈的相关性。我们还知道图像中相邻像素 x i 和 x j 的相关性很强。这种先验知识可以使用马尔科夫随机场模型进行描述,它的无向图如图8.31所示。
图中两种类型的团块
形如 {x i , y i } 的团块有一个关联的能量函数,表达了这些变量之间的相关性。对于这些团块,我们选择一个非常简单的能量函数 −ηx i y i ,其中 η 是一个正的常数。这个能量函数的效果是:当 x i 和 y i 符号相同时,能量函数会给出一个较低的能量(即,较高的概率),而当 x i 和 y i 符号相反时,能量函数会给出一个较高的能量。
(lz CRF t特征)由变量 {x i , x j } 组成的团块,其中 i 和 j 是相邻像素的下标。与之前一样,我们希望当两 个 像 素 符 号 相 同 时 能 量 较 低, 当 两 个 像 素 符 号 相 反 时 能 量 较 高, 因 此 我 们 选 择 能 量 函数 −βx i x j ,其中 β 是一个正的常数。
(lz CRF s特征)我们可以为无噪声图像的每个像素 i 加上一个额外的项 hx i 。这样的项具有下面的效果:将模型进行偏置,使得模型倾向于选择一个特定的符号,而不选择另一个符号。
模型的完整的能量函数的形式为
Note: 令 h = 0 意味着两个状态 x i 的先验概率是相等的。令 β = 0 ,从而去除了相邻像素点之间的联系,那么整体概率最大的解为 x i = y i (对于所有的 i ),这对应于观测到的噪声图像。
x 和 y 的联合概率分布,形式为
迭代条件峰值( iterated conditionalmodes, ICM)
( Kittler and Föglein, 1984 ) 为了恢复图像,我们希望找到一个具有较高概率(理想情况下具有最高概率)的图像 x 。
思想是,首先初始化变量 {x i } ,这个过程中我们只是简单地令 x i = y i 对于所有 i 都成立。然后,我们每次取一个 x j 结点,计算两个可能状态 x j = +1 和 x j = −1 的总能量,保持其他所有结点变量固定,将 x j 设置为能量较低的状态。如果 x j 不变,则概率不变,否则概率就会增大。由于只有一个变量发生改变,因此这是一个可以高效进行的简单局部计算。然后,我们对其他的结点重复更新过程,以此类推,知道满足某个合适的停止条件。结点可以用一种系统的方式更新,例如重复地依次扫描图像,或者随机地选择结点。如果我们有一个更新的顺序,使得每个像素都至少被访问一次,且没有变量发生改变,那么根据定义,算法会收敛于概率的一个局部最大值。
更加高效的算法寻找高概率的解,这种算法被称为最大加和算法,它通常会产生更好的解,虽然这种算法仍然不保证找到后验概率的全局最大值。
基于图割( graph cut )的高效的算法,保证找到全局的最大值( Greig et al., 1989; Boykov et al., 2001; Kolmogorov and Zabih, 2004 )。
from: http://blog.csdn.net/pipisorry/article/details/78396503
ref: [PRML]
[统计学习方法]
更详细的可参考[PGM:部分有向模型之条件随机场与链图模型 ]