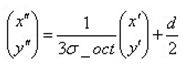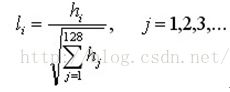SIFT算法的个人理解

SIFT算法的个人理解——理论篇

1. 前言

本人目前共使用过两个版本的sift算法:

（1）Matlab中的sift算法，可以从http://www.cs.ubc.ca/~lowe/keypoints/下载Lowe团队写的sift演示代码；

（2）opencv中的sift算法（本人使用的opencv版本是2.4.9），可以从http://opencv.org/下载opencv的各个版本，建议不要用太新的版本，容易出现一些小问题。本篇文章主要总结一下本人最近在做项目的过程当中学习和使用sift算法所遇到的问题，一方面可以和大家在网上交流学习，另一方面可以方便自己以后查阅和复习。

2.  SIFT中常见问题

首先还是介绍一下sift算法的主要步骤：（1）建立尺度空间，主要是指建立，Gaussian金字塔和DoG金子塔；（2）在尺度空间中寻找极值点（keypoints），并对其进行精确定位；（3）求解关键点的梯度幅值和幅角；（4）对关键点进行描述，形成128维的空间向量。

在步骤（1）当中大家需要明白的问题是：（1）什么是尺度？尺度空间中的尺度又是什么？（2）如何建立Gaussian金字塔？（3）如何建立DoG金字塔？（4）为什么要建立尺度空间，不建立尺度空间可以吗？这些问题也是我当初学习的时候遇到的问题，接下来就这些问题谈一谈我自己的认识，希望对大家有所帮助；

问题（1）我举一个简单的例子，相信大家就会明白了，比如你站在远处看一棵树木，你只能看见它的一簇树叶，而当你离树木越来越近的时候，你可以看见单个的树叶，而当你再靠近的时候，你就会看见树叶上的纹络。而在尺度空间当中的尺度在我理解是指图像的大小，对于同一张图像，图像的尺寸越大图像的尺度越大，图像越模糊；尺度越小图像越清晰。而图像中的细节可以在小的尺度上面找到，轮廓可以在大的尺度上面找到。

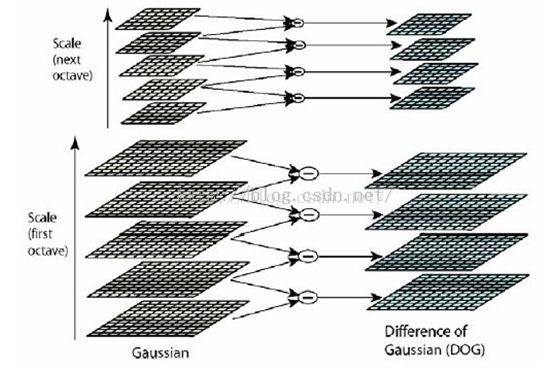
问题（2）建立高斯金字塔主要包括两个步骤：（a）对图像进行高斯模糊，即通过高斯掩膜对图像进行求卷积（b）对高斯模糊之后的图像进行降采样，即对图像中行和列的像素隔行删除。如示意图1所示

图1 Gaussian金字塔和DoG金字塔的建立示意图

图1左边的是Gaussian金字塔，右边的是DoG金字塔（后面会介绍到），图中octave--组，Layer--层，scale--尺度。如上图Gaussian第一组（first octave）中共有5层，包括0,1,2,3,4 ，第二组（second octave）中共有5层，包括0,1,2,3,4  。第一组的第0层是原始图像放大一倍后得到的，第1层是由第0层经过高斯平滑后得到的，... ，第4层是由第3层经过高斯平滑得到的；而第二组的第0层是由第1组的倒数第三张图像降采样得到的（这个地方是个难点，后面会讲到为什么是这个样子），接下来的步骤和第一组当中是一样的，不再赘述。   

问题（3）向大家介绍一下如何建立DoG金字塔，大家可以从上面的示意图看出，右边的DoG金字塔是通过左边的Gaussian金字塔同一组当中相邻两层相减而得到的，如：DoG金字塔的第1组第0层是通过第Gaussian金字塔的第1组第0层减去第1组的第1层得到的，依次类推。 

问题（4）  尺度空间理论的核心思想是通过对原始图像进行尺度变换，获得图像多尺度下的尺度空间序列，然后对这些序列进行主轮廓的提取，并以该主轮廓作为一种特征向量，实现边缘、角点（这个概念在后面会提到）提取。尺度空间的目的是模拟图像的多尺度特征，再说的简单一点，保证两幅图像在缩放的情况下也可以找到他们共同的特征点，从而能够实现算法的尺度不变性。

在步骤（2）当中大家需要明白的问题：（1）尺度空间连续是怎么回事？（2）如何在尺度空间寻找特征点？（3）尺度空间的极值点代表什么？为什么一定要找极值点而不找其他的点？

问题（1）

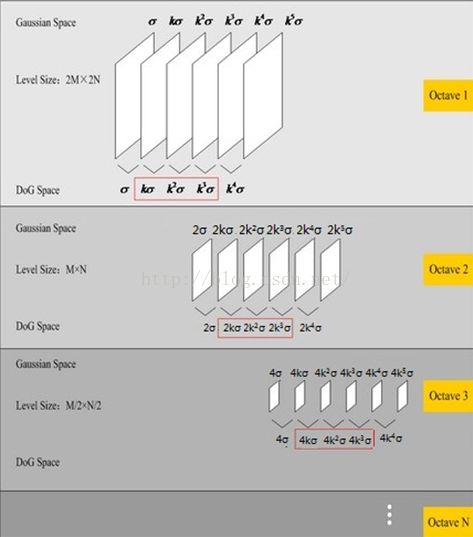
图2

可以发现以下规律：(a)尺度空间中同一组相邻2层之间的尺度倍数为k（k=2*（1/S）,S位尺度空间的组数，Lowe推荐S为3）；（b）尺度空间中相邻两组之间的尺度倍数为2（如第1组第0层尺度为sigma，第2组第0层尺度为2*sigma）；（3）Gaussian金字塔的的组数为S+3，DoG金字塔的组数为S+2，而最后寻找极值点的尺度空间为S；

上式中：

         sigma0----图像的初始尺度；

        O ----组数的索引值；

        r---每组层数的索引值；

        S---寻找极值点的尺度空间的组数，默认值为3；

 

下面开始进入正题，为什么说寻找极值点的尺度空间是连续的：为了帮助大家理解，帮大家画了一个简单的表格帮助大家理解

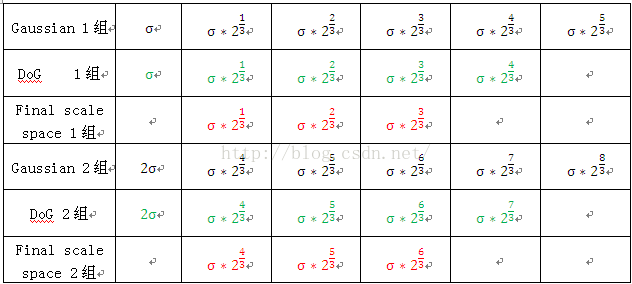
表1 尺度空间中的尺度

PS:在步骤一种提到“而第2组的第0层是由第1组的倒数第三张图像降采样得到的”这个时候可以告诉大家原因了，Gaussian1组的倒数第三张图像的尺度是，假设Gaussian2组的第一张图像是由此图片降采样得到的，可以得到Gaussian2组的第一张图像的尺度是；经过这样的采样可以保证Finalscale space是连续的。读者仔细观察表1就可以发现Final scale space 中的尺度是连续的：

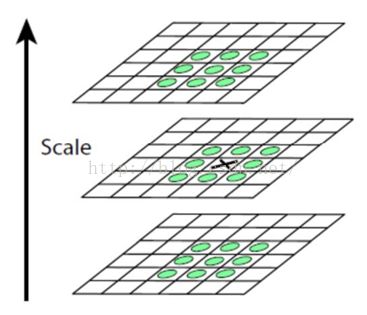
问题（2）：如图3所示

图3 尺度空间寻找极值点

如图3所示，尺度空间的特征点是在Final scale space同一组相邻3层寻找，将找到的特征点处的像素与上、中、下3层其他26个点相比较，通过寻找极小值和极大值，即尺度空间中的特征点。

问题（4）

尺度空间的极值点代表这样一类点，如：角点、暗区域的亮点以及亮区域的黑点，这些点是图像中十分突出的点，而且这些点相对比较稳定，在对两幅图像当中具有相同的物体进行SIFT特征点检测的时候，可以分别提取到这些稳定点，然后对这些进行特征点进行匹配。

在步骤3中，大家可能需要明白的问题包括：（1）特征点处的梯度幅值和幅角如何求解？（2）极值点处的主方向和辅方向分别代表什么？

问题（1）

上式中：

x,y---关键点在尺度空间中的位置坐标；

L(x，y)---（x，y）处的像素值；

问题（2）如图4所示

图4 关键点方向直方图

统计关键点直方图的区域半径：r=3*1.5 *sigma，其中sigma为关键点所在层相对于所在组的基准层的高斯尺度图像的尺度，即。而直方图的峰值就代表该关键点处的主方向，而辅方向是代表峰值大于主方向峰值80%以上的方向。在opencv中梯度直方图共有36个bins，上图只是代表示意图。

在步骤4中，大家可能需要明白的问题主要是一个：关键点周围的128维的向量是如何生成的？个人通过总结主要包括以下几步：

（1）  确定计算特征描述符的邻域范围

以特征点为中心周围的d*d个子区域为计算范围，值得注意的是这里的子区域的大小并不是一个像素而边长为的正方形区域，，理论上区域中的像素个数为：，opencv当中区域中实际像素个数为：个。为了保证特征点具有旋转不变性，后来还会对图像进行旋转一个角度，为了保证旋转之后的区域能够包括之前的整个正方形，所以 旋转之后区域大小半径为。

（2）  图像旋转

如图5所示

图5 图像旋转

       而在实际编程中为了计算方便会将得到的坐标进行单位化，如下面的公式所示：

而上面的公式加上d/2的原因为了将特征点领域范围的坐标原点从中心位置移动到左下角，方便后面编程。

（3）  对关键点周围半径区域内的每个像素点求取其梯度幅值和方向，然后对每一个梯度幅值乘以高斯权重参数，生产3维直方图。求取高斯权重参数的时候较为复杂，如果有兴趣了解的朋友可以和我私下讨论。

（4）  对计算得到的128维向量，进行单位化，就可以得到最终的特征描述符，如下面的公式所示：

3.  其他参考资料

1.http://blog.csdn.net/zhaocj/article/details/42124473（对SIFT的源代码有详细的解释，是目前本人阅读过SIFT最详细的参考资料了）

2.http://www.360doc.com/content/14/1013/15/18306241_416576994.shtml（写的十分详细，对于初学者理解SIFT十分有用）

3. http://www.cs.ubc.ca/~lowe/keypoints/(sift 官网，可以在下面下载SIFT论文以及作者的源代码是，代码是Matlab版本的)。

4. 《图像局部不变性特征与描述》，作者王永明，王贵锦。（此书对于想研究图像中局部特征描述子的朋友可以好好的读一下，书中对于SIFT SURF SUSAN等兴趣点检测的方法都提到了，并且讲解的十分详细）

还有很多关于SIFT资料，我就不一一列举了，大家有兴趣的话可以自己搜索。

4.  总结

自己在这篇博客简单总结了在研究和使用SIFT期间所遇到的问题，只是想和大家分享自己的见解，可能并不是很专业，但是本人会继续努力的，会在后期不断完善和修正这篇博客。

 

PS:这是本人第一次写博客，写的不好还请大家见谅，我很乐意和大家一起讨论问题，大家如果有什么疑问，可以私信我,我的邮箱[email protected]

@2018.2.4  对本博文进行第一次修改，感谢yingshi.ma所提出的建议。