图像处理基本知识
1.图像处理方法分类
| 输入 | 输出 | 等级 | 例子 |
|---|---|---|---|
| 图像 | 图像 | 初级 | 降噪,增强对比度 |
| 图像 | 图像特征 | 中级 | 轮廓提取 |
| 图像 | 图像表征的信息 | 高级 | 模式识别,机器视觉 |
2. 图像增强(image enhancement)
- 没有统一的图像增强算法,要针对具体问题具体分析,用户是最终标准的评判者;用户说好就是好,所以没有所谓”最好 ”的图像增强算法。
3. 像素点之间的关系
| 名称 | 表示法 | 包括点 |
|---|---|---|
| 4邻域(4-neightbors) | N4(p) | {2,4,5,7} |
| D邻域(d-neightbors) | ND(p) | {1,3,6,8} |
| 8邻域(8-neightbors) | N8(p) | {1,2,3,4,5,6,7,8} |
4. 邻接(adjacency)、连通(connectivity)、区域(regions) 、边界(boundaries)
4.1 邻接
邻接有的书上翻译叫连接,其实是一个意思。这就体现了看英文资料的好处,没有翻译导致的奇异。
设 f(p) 和 f(q) 分别表示像素点p、q的强度,V表示函数 f() 全体值域的y一个子集,则
| 名称 | 定义 |
|---|---|
| 4邻接(4-adjacency) | f(p)∈V∧f(q)∈V∧q∈N4(p) |
| 8邻接(8-adjacency | f(p)∈V∧f(q)∈V∧q∈N8(p) |
| m邻接(m-adjacency) | 1. f(p)∈V∧f(q)∈V 2. q∈N4(p) or q∈ND(p)∧(N4(p)∩N4(q))∉V |
m邻接又称为混合邻接,其作用是为了消除8邻接导致的多路问题。
为了解释这个多路问题,需要引入路径的概念。路径(path)是一系列像素点的集合,相邻的俩个像素点的关系要满足一种邻接的定义。比如4邻接路径,就表示路径中相邻两个像素点满足4邻接关系。8邻接路径、m邻接路径的定义与此类似。
假设V={1},则各种邻接的路径如下图所示:
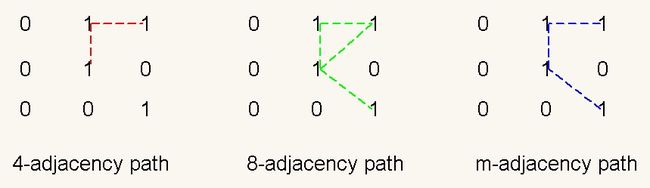
可以看出8邻接路径存在多路的问题。
4.2 连通
设S为图像中部分像素的集合
如果可以在S中找到一条路径连接像素点p和q,则称p和q 在S中是连通的。自然,根据路径选择方法的不同,连通也应该分为4连通,8连通和m连通。
在S中,对于任意的像素点p,所有与p点连通的像素点的集合(包括p点)称为一个连通组件。如果在S中只能找到一个连通组件,则称S为连通集合。
4.3 区域
图像中的一个连通集合也可以叫做一个区域。自然,依据使用的连通类型不同,区域也分为4连通区域,8连通区域(原则上讲也应该有m连通区域,但在涉及区域的问题讨论中很少应用m连通)。
如果两个4连通区域可以合并为一个更大的4连通区域,则称这两个区域是4邻接的。相应的,也存在8邻接。
如果两个类型相同的连通区域无法合并,则称这两个连通区域是不想交的(disjoint)。
ps:在同一副图像上划分区域时,只会采用一种连通类型。要么都是4连通的,要么都是8连通的。不会出现我把图像的左边划分为4连通的,右边划分为8连通的情况。
4.4 前景(foreground)和背景(background)
假设在一副图像上有k个不想交的区域。
设Ru等于所有者k个区域的集合,(Ru)c等于图像上Ru以外的像素点的集合。
则,Ru称为图像的前景,(Ru)c称为Ru的背景。(这个相对性很重要,背景是针对前景而言的)
4.5 边界(boundary,border)
如果区域R中存在像素点p,且p点的领域中至少有一个像素点落在R的背景中,则R中所有这样的点P组成的集合叫做区域R的边界。
根据上面的定义,自然也存在4连通边界和8连通边界的说法。但更多使用的是8连通边界,否则如下图中红圈圈出的点将不被认为是边界,这很不自然。

以上方式定义的区域的内边界,响应的,在背景中与内边界相邻的点组成的集合称为外边界。
5. 距离
两个像素点间的距离计算方式,常见的有三种,定义如下:
De(p,q)=(p.x−q.x)2+(p.y−q.y)2−−−−−−−−−−−−−−−−−−−−−−√
D4(p,q)=|p.x−q.x|+|p.y−q.y|
D8(p,q)=max(|p.x−q.x|,|p.y−q.y|)
6. gamma校正
6.1 gamma校正的定义
首先介绍一下变换函数
其中
r—某个像素点的强度;
c—为尝试;
γ —为变换参数;
s—此像素点变换后的强度;
利用以上公式对输入图像的每个像素点进行处理的过程称为gamma校正。
6.2 gamma校正的作用
1.修复图像失真
下图展示了一副自然界图像经电子设备呈现在人眼上的过程

如果自然界图像经过传感器直接转化为数字图像时,会发生失真。这种失真是由于传感器硬件引起的,无法避免。经验上可以将失真总结为如下的形式:
为了弥补这种失真,可以在步骤2增加一部gamma校正,即:
经过这样的校正,数字图像和自然界图像就相同了。
可以看出,校正的关键是 α 值的选择。这个值一般由传感器的生成厂家根据自身产品的特点固化在传感器里,对传感器的用户来说,是不需要关系的。
2.增加对比度
下图展示了不同 γ 下,输入与输出的关系

可以看出当 γ<1 时,会增强原图像中暗处的对比度;
可以看出当 γ==1 时,无任何效果;
可以看出当 γ>1 时,会增强原图像中亮处的对比度;
但是对强度的影响是非线性的。
7. 灰度分层(intensity-level slicing)
8.Bit平面分层(bit-plane slicing)
概念上比较抽象,举个例子来理解。
假设每一个像素点由2bit组成,一副图像有4个像素点。则如下图所示,图像1可以由图像2和图像3叠加而来。

那么,图像2和图像3就是图像1的两个bit平面。
同理可以推断出,如果每个像素点由8个bit组成,则一副图像应该有8个bit平面。
bit平面分层可以用于图像的有损压缩,通过这种分析你可以发现,有些bit平面对图像的贡献是很小的,删除这一层的数据,人眼是无法分辨的,但这样就节约了空间以及传输的数据量。
9.直方图(histogram)处理
1.图像的直方图
图像的直方图实际上就是图像不同强度的像素点的概率分布图。
假设一副8bit图像(8bit图像指图像的每个像素点用8bit长度的数据表示,共可以表示0~255,共计256个强度)有M*N个像素点。
令n255表示强度的255的点,在图像中的数量,则此图像强度为255的概率可根据如下公式计算:
同理可以计算出P 0~P 255的值,然后以强度为x轴,概率为y轴绘制的直方图,就是此图像的直方图。
通过图像的直方图可以看出以下几点结论:
1. 图像亮度较暗,则直方图集中在x轴的左侧;
2. 图像亮度较亮,则直方图集中在x轴的右侧;
3. 图像对比度较低,则直方图集中在某个很小的范围内;
4. 图像对比度较高,则直方图均匀分布在整个x轴。
2.直方图均衡
根据上一节的结论4,“图像对比度较高,则直方图均匀分布在整个x轴”。我们可以将一个对比度较低的图像,通过某种变化,使其直方图均匀分布,这样就可以增进对比度。这其中最简单的算法是“直方图均衡”。
令 s=T(r) ,其中 s 表示转换后的像素点强度, r 表示原像素点强度。如果 T(r) 是连续可微函数,则有如下结论:
基于以上的结论,我们可以构造如下的转换函数:
基于以上构造的转换函数,我们很容易计算出
3.自由选择输出图像的概率密度函数
上一节中构造的转换函数,转换后图像的概率密度是常数。这在多数情况下已经足够好,但有时我们希望自由选择输出图像的概率密度函数。
下面直接介绍算法:
1. 令变换后的概率密度函数为 Pz(z) ;
2. 令 s1=(N−1)∫z0Pz(w)dw , s2=(N−1)∫r0Pr(w)dw ;
3. 由于 Pr(r) 和 r 是输入图像的数据,是已知的,我们可以计算出 {(s2,r)} 的对应关系表;
4. 由于 Pz(z) 是我们选定的, z 的取值范围是 [0,2n−1] ,所以可以得到 {(s1,z)} 的对应关系表;
5. 基于以上几点可知,当有一个输入 r ,便可以查询到一个 s2 ,然后选择 |s2−s1| 最小的 s1 ,再根据这个 s1 得到 z ,即完成了变换。