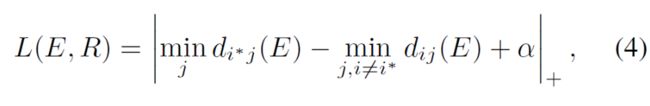CVPR19目标检测

前言

阅读CVPR2019并总结

CVPR2019目标检测方法进展综述

2、Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression

论文链接：https://arxiv.org/abs/1902.09630

论文解读：https://mp.weixin.qq.com/s/6QsyYtEVjavoLfU_lQF1pw

一开始目标检测回归的框是用L2 loss来进行的,但是会尺度敏感,也就是:

于是用IOU loss代替(IOU loss原文:《2016 ACM MM UnitBox: An Advanced Object Detection Network》),实验结论：收敛更快，对尺度更鲁棒。

但是IOU loss还有问题,这里提到的训练不稳定,GIOU论文提到的IOU_loss无法正确区分两个框不同方向的重合

参考:https://blog.csdn.net/shuzfan/article/details/52625449

-------------------------------------------------------------------------------------------------------------------------

4、Bi-Directional Cascade Network for Perceptual Edge Detection

论文链接：https://arxiv.org/abs/1902.10903

Github源码：https://github.com/pkuCactus/BDCN

解读:https://blog.csdn.net/qq_34914551/article/details/89739256

多尺度预测解决边缘检测的问题,把label根据不同层有不同的划分大小,划分依据由网络自己学,学习方法是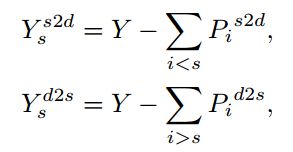即监督是其它层的输出结果,每层两个loss,shallow2deep and deep2shallow

=============================================================

5、RepMet: Representative-based metric learning for classification and one-shot object detection

论文链接：https://arxiv.org/abs/1806.04728

此文有关度量学习(distance metric learning),称为相似度学习会更容易理解,即判断两张照片是否为同一类,在reidentification任务中应用广泛,可分为人为定义度量和神经网络训练度量两种,本文为后者

本文贡献;提出了一个度量学习的subnet architecture和对应的loss,此subnet可应用于obejct detection和classification任务中;可直接代替detection中的classification头,作者在上述提到的两种任务中都做了实验

网络结构如下

DML embedding模块实际是FC layer与一些激活层(detection实验中的是一层1024与一层2048FCL),值得注意的是作者将N类,每类又分为了K个mode(解决类内差异)来表示多模(multi-modal).compute distance是计算class representatives到embeded feature vector的距离,(这两个都能在图中看到)而计算出的距离是通过以下式子来计算概率值的

(mixing coefficient是什么意思....)

最终算出来的物体属于哪一类,把Pij转化为类别的过程没有学习mixing coefficient,而是通过最大值的j属于哪一类来决定的,如上图,这个条件概率是在actual class posterior的上界(不知是否可理解为一个threshold)

(若最大值都小于下界,则被认为是背景目标(没专门设置背景类,这样就可以不用在训练时额外取样了)),

而没有学习mixing coefficient的原因:在测试的时候,representatives被新类的embedded空间替代,而mixture coefficient与特定的mode有关,在测试的时候mode会改变,所以学习mixing coefficient就很non-trivial.用了式子2中的上界就能避免学习mixture系数

Loss:两个,gt与prediction的交叉熵与类间度量的损失(如图4)

后者旨在pred和label的representative距离最高为阿尔法,pred与最近的错误的类距离也要大于阿尔法

---------------------------------------------