面试算法题目

１、二叉树的之字形打印

请实现一个函数按照之字形打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右至左的顺序打印，第三行按照从左到右的顺序打印，其他行以此类推。

# -*- coding:utf-8 -*-
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    def Print(self, pRoot):
        if not pRoot:
            return []
        nodeStack=[pRoot]
        result=[]
        while nodeStack:
            res = []
            nextStack=[]
            for node in nodeStack:
                res.append(node.val)
                if node.left:
                    nextStack.append(node.left)
                if node.right:
                    nextStack.append(node.right)
            nodeStack=nextStack
            result.append(res)
        returnResult=[]
        for i,v in enumerate(result):
            if i%2==0:
                returnResult.append(v)
            else:
                returnResult.append(v[::-1])
        return returnResult

 

２、最大连续子序列

https://www.nowcoder.com/questionTerminal/afe7c043f0644f60af98a0fba61af8e7

　　给定K个整数的序列{ N1, N2, ..., NK }，其任意连续子序列可表示为{ Ni, Ni+1, ..., Nj }，其中 1 <= i <= j <= K。最大连续子序列是所有连续子序列中元素和最大的一个，例如给定序列{ -2, 11, -4, 13, -5, -2 }，其最大连续子序列为{ 11, -4, 13 }，最大和为20。现在增加一个要求，即还需要输出该子序列的第一个和最后一个元素。

 

#-*-coding:utf-8-*-
n = int(input())
nums = list(map(int, input().strip().split()))


def Solution(nums):
    maxsum = nums[0]
    res = []

    for i in range(n):
        for j in range(i, n):
            cur = nums[i:j]
            addsum = sum(cur)
            if addsum > maxsum:
                maxsum = addsum
                res.append(cur)
    return [maxsum, res[-1][0], res[-1][-1]]

if __name__ == '__main__':
    res = Solution(nums)
    print(res)

最大子序和

 dp问题. 公式为: dp[i] = max(nums[i], nums[i] + dp[i - 1])

class Solution:
    def maxSubArray(self, nums):
        n = len(nums)
        dp = nums
        for i in range(1, n):
            dp[i] = max(dp[i - 1] + nums[i], nums[i])
        return max(dp)

在简单一点

def maxSubArray(nums):
    """
        1. dp问题. 公式为: dp[i] = max(nums[i], nums[i] + dp[i - 1])
        2. 最大子序和 = 当前元素自身最大, 或者 包含之前后最大
    """
    for i in range(1, len(nums)):
        # nums[i-1]代表dp[i - 1]
        nums[i] = max(nums[i], nums[i] + nums[i-1])
        
    return max(nums)

 

３、翻转链表（６６道里面有）

https://www.nowcoder.com/questionTerminal/75e878df47f24fdc9dc3e400ec6058ca

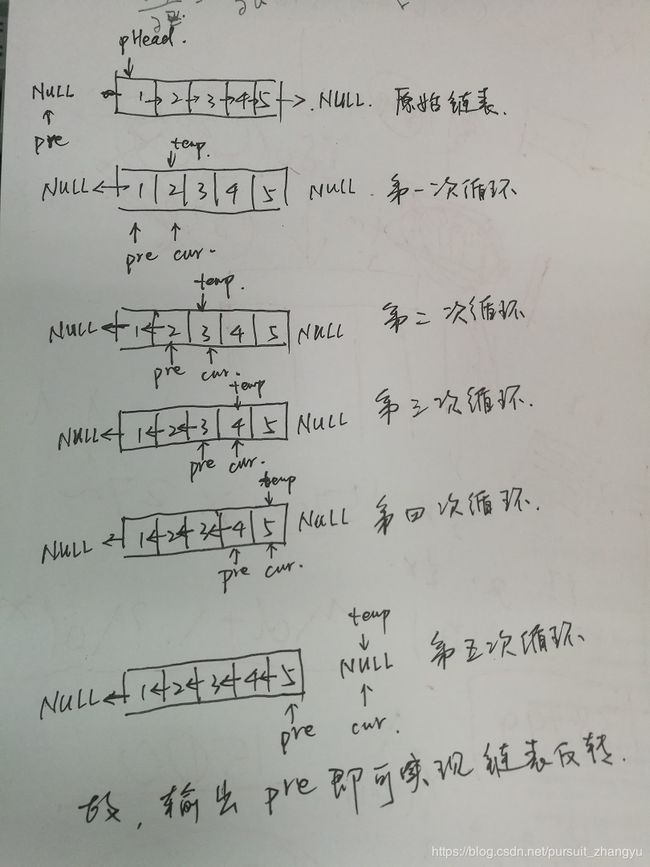
输入一个链表，反转链表后，输出新链表的表头。

# -*- coding:utf-8 -*-
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
class Solution:
    # 返回ListNode
    def ReverseList(self, pHead):
        # write code here
        if not pHead or not pHead.next:
            return pHead
        pre = None
        while pHead:
            tmp = pHead.next
            pHead.next = pre
            pre = pHead
            pHead = tmp
        return pre

４、列表topK数字，要求复杂度最优

堆排序吧

５、输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字，例如，如果输入如下4 X 4矩阵： 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 则依次打印出数字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10.

牛客６６到里面第１９题

https://blog.csdn.net/pursuit_zhangyu/article/details/94591035

６、由0和1组成的二维矩阵，找出1的最大连通域，计算其面积

leetcode695题

https://leetcode-cn.com/problems/max-area-of-island/solution/python-dfs-time955-by-zuo-lun-jiu-shi-wo/

解题

https://blog.csdn.net/weixin_40449300/article/details/83378927

给定一个包含了一些 0 和 1的非空二维数组 grid , 一个 岛屿 是由四个方向 (水平或垂直) 的 1 (代表土地) 构成的组合。你可以假设二维矩阵的四个边缘都被水包围着。

找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为0。)

示例 1:

[[0,0,1,0,0,0,0,1,0,0,0,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]

对于上面这个给定矩阵应返回 6。注意答案不应该是11，因为岛屿只能包含水平或垂直的四个方向的‘1’。

示例 2:

[[0,0,0,0,0,0,0,0]]

对于上面这个给定的矩阵, 返回 0。

注意: 给定的矩阵grid 的长度和宽度都不超过 50。

 

解题思路：
很明显看出是利用DFS解：遍历二维数组，当值为1时开始dfs，搜索的时候有上下左右四个方向(nextSteps)，每当走过一个相邻的1（岛屿）就标记一下（改成-1），这样下次就不会走之前走过的岛屿了。

#-*-coding:utf-8-*-
class Solution(object):
    def __init__(self):
        self.area = 0
    def NumOfIsland(self, grid):
        m = len(grid)
        n = len(grid[0])
        max_area = 0
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 1:
                    self.area = 0
                    self.infect(grid, i, j, m, n)
                    max_area = max_area if self.area < max_area else self.area
        return max_area

    def infect(self, grid, i, j, m, n):
        if i < 0 or i >= m or j < 0 or j >= n or grid[i][j] != 1:
            return
        grid[i][j] = -1
        self.area += 1
        self.infect(grid, i + 1, j, m, n)
        self.infect(grid, i - 1, j, m, n)
        self.infect(grid, i, j + 1, m, n)
        self.infect(grid, i, j - 1, m, n)


so = Solution()
res = so.NumOfIsland(grid=[[0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
                           [0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0],
                           [0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
                           [0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0],
                           [0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0],
                           [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0],
                           [0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0],
                           [0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0]])
print(res)

 

class Solution(object):
    nextStep = [[0, 1], [1, 0], [0, -1], [-1, 0]]
    step = 0
    def maxAreaOfIsland(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        res = 0
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if grid[i][j] == 1:
                    self.step = 0
                    self.dfs(grid, i, j)
                    res = max(res, self.step)
 
        return res
 
    def dfs(self, grid, x, y):
        """
        :type grid: List[list[int]]
        :type x: int
        :type y: int
        :rtype : None
        """
        if x < 0 or y < 0 or x > len(grid) - 1 or y > len(grid[0]) - 1 or grid[x][y] != 1:
            return
        grid[x][y] = -1
        self.step += 1
        for i in range(len(self.nextStep)):
            self.dfs(grid, x + self.nextStep[i][0], y + self.nextStep[i][1])

求岛屿的个数

#-*-coding:utf-8-*-
class Solution(object):
    def NumOfIsland(self, grid):
        m = len(grid)
        n = len(grid[0])
        res = 0
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 1:
                    res += 1
                    self.infect(grid, i, j, m, n)
        return res

    def infect(self, grid, i, j, m, n):
        if i < 0 or i >= m or j < 0 or j >= n or grid[i][j] != 1:
            return
        grid[i][j] = -1
        self.infect(grid, i + 1, j, m, n)
        self.infect(grid, i - 1, j, m, n)
        self.infect(grid, i, j + 1, m, n)
        self.infect(grid, i, j - 1, m, n)


so = Solution()
res = so.NumOfIsland(grid=[[0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
                           [0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0],
                           [0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
                           [0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0],
                           [0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0],
                           [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0],
                           [0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0],
                           [0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0]])
print(res)

7、连续子数组的最大和

例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。给一个数组，返回它的最大连续子序列的和，

 

动态规划初级题目,做完之后,可以试试最大子矩阵和(https://www.nowcoder.com/questionTerminal/a5a0b05f0505406ca837a3a76a5419b3)

该题目思路:

dp[i]表示以元素array[i]结尾的最大连续子数组和.

以[-2,-3,4,-1,-2,1,5,-3]为例

可以发现,

dp[0] = -2

dp[1] = -3

dp[2] = 4

dp[3] = 3

以此类推,会发现

dp[i] = max{dp[i-1]+array[i],array[i]}.

# -*- coding:utf-8 -*-
class Solution:
    def FindGreatestSumOfSubArray(self, array):
        m = len(array)
        dp = [i for i in array]
        for i in range(1, m):
            dp[i] = max(dp[i-1]+array[i], array[i])
        return max(dp)

８、二维数组回行打印

# -*- coding:utf-8 -*-
class Solution:
    def printMatrix(self, matrix):
        # write code here
        result = []
        while (matrix):
            result += matrix.pop(0)
            if not matrix:
                break
            matrix = self.turn(matrix)
        return result
 
    def turn(self, matrix):
        newmat = []
        row = len(matrix)
        col = len(matrix[0])
        for i in range(col):
            newmat1 = []
            for j in range(row):
                newmat1.append(matrix[j][i])
            newmat.append(newmat1)
        newmat.reverse()
        return newmat

8、合并两棵二叉树，对于两棵树都存在的节点，节点值相加，否则空的位置用另一棵树的节点来代替

 

9、KMP 算法

暴力解法

#-*-coding:utf-8-*-
def match(str1, str2):
    n = len(str1)
    m = len(str2)
    for i in range(n-m+1):
        for j in range(m):
            print(str1[i:i+m])
            if str1[i:i+m] == str2:
                return True
    return False

str1 = 'abababca'
str2 = 'ababca'
res = match(str1, str2)
print(res)

ＫＭＰ算法

def kmp(str1, str2):
    next = get_next(str2)
    i = j = 0
    while i < len(str1) and j < len(str2):
        if str1[i] == str2[j]:
            i += 1
            j += 1
        elif next[j] == -1:
            i += 1
        else:
            j = next[j]
    if len(str2) == j:
        return i-j
    else:
        return -1

def get_next(str2):
    next = [0 for i in range(len(str2))]
    if len(str2) == 1:
        return [-1]
    next[0] = -1
    next[1] = 0
    i = 2
    cn = 0
    while i < len(str2):
        if str2[i-1] == str2[cn]:
            next[i] = cn+1
            i += 1
            cn += 1
        elif cn > 0:
            cn = next[cn]
        else:
            next[i] = 0
            i += 1
    return next

str1 = 'ababcabcac'
str2 = 'abcac'
res = kmp(str1, str2)
print(res)

kmp算法加速匹配.算法的依据是，子串里面有一定的规律，next数组就是里面的规律（最大前缀的最大后缀关系）

10、两个有序数组的合并

#-*-coding:utf-8-*-
def merge(array1, array2):
    res = []
    while array1 and array2:
        if array1[0] < array2[1]:
            res.append(array1.pop(0))
        else:
            res.append(array2.pop(0))
        while array1:
            res.append(array1.pop(0))
        while array2:
            res.append(array2.pop(0))
    return res

11、接雨水

https://mp.weixin.qq.com/s?__biz=MzUyNjQxNjYyMg==&mid=2247486391&idx=2&sn=f6c2f140cc12799239d555da4f417b43&chksm=fa0e6436cd79ed20055a8cbb85916d846f614ecf36d1f243631769c3885818597082a211394b&mpshare=1&scene=1&srcid=&sharer_sharetime=1568009869136&sharer_shareid=c21f8d7eea5ad2a9454577d10f826069#rd

#-*-coding:utf-8-*-
#暴力解法
def tracp(array):
    res = 0
    for i in range(len(array)):
        l_max = max(array[0:i+1])
        r_max = max(array[i:])
        res += min(l_max, r_max) - array[i]
    return res

#双指针解法
def tracp1(array):
    res = 0
    left = 0;right = len(array)-1
    l_max = array[0];r_max = array[-1]
    while left <= right:
        l_max = max(l_max, array[left])
        r_max = max(r_max, array[right])
        if l_max <= r_max:
            res += l_max - array[left]
            left += 1
        else:
            res += r_max - array[right]
            right -= 1
    return res

array = [0,1,0,2,1,0,1,3,2,1,2,1]
res = tracp1(array)
print(res)

12. 最小路径和

https://leetcode-cn.com/problems/minimum-path-sum/solution/zui-xiao-lu-jing-he-dong-tai-gui-hua-gui-fan-liu-c/

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

输入:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

 

class Solution:
    def minPathSum(self, grid: [[int]]) -> int:
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if i == j == 0: continue
                elif i == 0:  grid[i][j] = grid[i][j - 1] + grid[i][j]
                elif j == 0:  grid[i][j] = grid[i - 1][j] + grid[i][j]
                else: grid[i][j] = min(grid[i - 1][j], grid[i][j - 1]) + grid[i][j]
        return grid[-1][-1]

暴力递归的方法 

# -*-coding:utf-8-*-
class Solution:
    def walk(self, matrix, i, j):
        if i == len(matrix) - 1 and j == len(matrix[0]) - 1:
            return matrix[i][j]
        if i == len(matrix) - 1:
            return matrix[i][j] + self.walk(matrix, i, j + 1)
        if j == len(matrix[0]) - 1:
            return matrix[i][j] + self.walk(matrix, i + 1, j)
        right = self.walk(matrix, i, j + 1)
        down = self.walk(matrix, i + 1, j)
        return matrix[i][j] + min(right, down)


matrix = [[1, 3, 1],
          [1, 5, 1],
          [4, 2, 1]]
so = Solution()
res = so.walk(matrix, i=0, j=0)
print(res)

13、最长公共子序列

https://www.nowcoder.com/questionTerminal/02e7cc263f8a49e8b1e1dc9c116f7602

14、TopK问题

https://zhuanlan.zhihu.com/p/76734219

先用前k个元素生成一个小顶堆，这个小顶堆用于存储，当前最大的k个元素。
接着，从第k+1个元素开始扫描，和堆顶（堆中最小的元素）比较，如果被扫描的元素大于堆顶，则替换堆顶的元素，并调整堆，以保证堆内的k个元素，总是当前最大的k个元素。

#-*-coding:utf-8-*-
class Solution:
    def topk(self, arr, k):
        arr1 = arr[:k]
        for i in range(k//2-1, -1, -1):
            self.heapify(arr1, i)

        for i in range(k, len(arr)):
            if arr[i] > arr1[0]:
                arr1[0] = arr[i]
                self.heapify(arr1, 0)
        return arr1


    def heapify(self, arr1, i):
        left = 2*i + 1
        right = 2*i + 2
        min = i
        if left < len(arr1) and arr1[left] < arr1[min]:
            min = left
        if right < len(arr1) and arr1[right] < arr1[min]:
            min = right
        if min != i:
            arr1[i], arr1[min] = arr1[min], arr1[i]
            self.heapify(arr1, min)


so = Solution()
arr = [5, 3, 7, 1, 8, 2, 9, 4, 7, 2, 6, 6]
res = so.topk(arr, 8)
print(res)

15.python实现split方法

https://blog.csdn.net/wangweimic/article/details/90600820

关键点在与使用了find方法

def split_t(txt, delimeter):
    tempstr = []
    lengstring = len(txt)
    lengchar = len(delimeter)

    for i in range(lengstring):
        index = txt.find(delimeter)
        if index == -1:
            tempstr.append(txt)
            return tempstr
        else:
            tempstr.append(txt[:index])
            txt = txt[index + lengchar:]

if __name__ == "__main__":
    print(split_t("ABGHFTRRFDSHSYTSFSGAFDVR", "HF"))

>>> st = 'abc'
>>> st.find('b')
1
>>> st1 = ''
>>> st1.find('b')
-1

16. 无序数组找中位数

通过构建最小堆来求解

思想是：

1 对无序数组的前len(array)//2长度的元素建立最小堆，这样就得到了一个堆顶元素小于任意一个堆里的元素

2 将剩下的一半元素依次与堆顶元素比较。若比堆顶元素大，则替换之，并调整堆。（也就是说：依次遍历剩下一般的元素，与当前的堆顶元素作比较，如果大于堆顶元素，则替换，这时，重新调整堆的结构，使其保持为最小堆，否则，遍历下一个元素，知道剩下的一半元素遍历结束）

3 数组剩下的所有元素比较完后，可以输出中位数。数组长度为奇数时，输出堆顶元素即可。数组长度为偶数时，输出堆顶元素与它的孩子结点中较小的那个的均值。
 

# coding:utf-8
def heap_adjust(parent, heap):  # 更新结点后进行调整
    child = 2 * parent + 1
    while len(heap) > child:
        if child + 1 < len(heap) and heap[child + 1] < heap[child]:
            child += 1
        if heap[parent] <= heap[child]:
            break
        heap[parent], heap[child] = heap[child], heap[parent]
        parent, child = child, child * 2 + 1


def find(nums):
    k = len(nums) // 2 + 1
    heap = nums[:k]
    for i in range(k, -1, -1):  # 前n/2个元素建堆
        heap_adjust(i, heap)
    for j in range(k, len(nums)):
        if nums[j] > heap[0]:
            heap[0] = nums[j]
            heap_adjust(0, heap)
    # 奇数时是最中间的数，偶数时是最中间两数的均值
    return heap[0] if len(nums) % 2 == 1 else float(heap[0] + min(heap[1], heap[2])) / 2


print(find([1, 2, 8, 9, 3, 5, 4, 6, 7, 0]))
print(find([1, 3, 2, 4]))

 17. 翻转字符串

编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。

不要给另外的数组分配额外的空间，你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。

你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。

class Solution:
    def reverseString(self, s: List[str]) -> None:
        """
        Do not return anything, modify s in-place instead.
        """
        i = 0
        j = len(s) - 1
        while (i < j):
            s[i], s[j] = s[j], s[i]#交换赋值
            i+=1
            j-=1

其实py3有很多好玩的操作，比如这道题可以这样：s=list(reversed(s)) 因为 reversed() 函数返回的是一个迭代器，所以要用 list() 函数才行。但是速度不快。

如果是字符串反转而不是数组还可以这样 s=s[::-1] （字符串切片：string[start:stop:step]）

18. 删除排序链表中的重复元素(leetcode83)

给定一个排序链表，删除所有重复的元素，使得每个元素只出现一次。

示例 1:

输入: 1->1->2
输出: 1->2

示例 2:

输入: 1->1->2->3->3
输出: 1->2->3

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def deleteDuplicates(self, head: ListNode) -> ListNode:
        if head == None or head.next == None:
            return head
        phead = head
        while True:
            if phead.val == phead.next.val:
                phead.next = phead.next.next
            else:
                phead = phead.next
            if phead.next == None:
                break
        return head

19. 在数组中找到第 k 大的元素。要求时间复杂度为O(n),空间复杂度为O(1)

leetcode215

https://leetcode-cn.com/problems/kth-largest-element-in-an-array/solution/ji-yu-kuai-pai-shi-xian-shi-jian-fu-za-du-on-by-re/

思路如下，每次排序将大于基准值key的放key的左边，将小于基准值key的放key的右边。
然后如果基准值所在的位置正好=k-1.则正好就是这个值
如果左边的数量

class Solution:
    def findKthLargest(self, nums, k):
        n = len(nums)
        if n == 0 and k > n:
            return 0
        return self.find(nums, 0, n - 1, k)

    def find(self, nums, left, right, k):
        start = left
        end = right
        key = nums[start]
        while start < end:
            while start < end and nums[end] <= key:
                end -= 1
            nums[start] = nums[end]
            while start < end and nums[start] >= key:
                start += 1
            nums[end] = nums[start]
        nums[start] = key
        if start == k - 1:
            return key
        elif start < k - 1:
            return self.find(nums, start + 1, right, k)
        else:
            return self.find(nums, left, start - 1, k)

20.100亿数据找出最大的1000个数字

1、最容易想到的方法是将数据全部排序。该方法并不高效，因为题目的目的是寻找出最大的10000个数即可，而排序却是将所有的元素都排序了，做了很多的无用功。

2、局部淘汰法。用一个容器保存前10000个数，然后将剩余的所有数字一一与容器内的最小数字相比，如果所有后续的元素都比容器内的10000个数还小，那么容器内这个10000个数就是最大10000个数。如果某一后续元素比容器内最小数字大，则删掉容器内最小元素，并将该元素插入容器，最后遍历完这1亿个数，得到的结果容器中保存的数即为最终结果了。此时的时间复杂度为O（n+m^2），其中m为容器的大小。

这个容器可以用（小顶堆）最小堆来实现。我们知道完全二叉树有几个非常重要的特性，就是假如该二叉树中总共有N个节点，那么该二叉树的深度就是log2N，对于小顶堆来说移动根元素到 底部或者移动底部元素到根部只需要log2N，相比N来说时间复杂度优化太多了（1亿的logN值是26-27的一个浮点数）。基本的思路就是先从文件中取出1000个元素构建一个小顶堆数组k，然后依次对剩下的100亿-1000个数字进行遍历m，如果m大于小顶堆的根元素，即k[0]，那么用m取代k[0]，对新的数组进行重新构建组成一个新的小顶堆。这个算法的时间复杂度是O((100亿-1000)log(1000))，即O((N-M)logM)，空间复杂度是M

这个算法优点是性能尚可，空间复杂度低，IO读取比较频繁，对系统压力大。

3、第三种方法是分治法，即大数据里最常用的MapReduce。

a、将100亿个数据分为1000个大分区，每个区1000万个数据

b、每个大分区再细分成100个小分区。总共就有1000*100=10万个分区

c、计算每个小分区上最大的1000个数。

为什么要找出每个分区上最大的1000个数？举个例子说明，全校高一有100个班，我想找出全校前10名的同学，很傻的办法就是，把高一100个班的同学成绩都取出来，作比较，这个比较数据量太大了。应该很容易想到，班里的第11名，不可能是全校的前10名。也就是说，不是班里的前10名，就不可能是全校的前10名。因此，只需要把每个班里的前10取出来，作比较就行了，这样比较的数据量就大大地减少了。我们要找的是100亿中的最大1000个数，所以每个分区中的第1001个数一定不可能是所有数据中的前1000个。

d、合并每个大分区细分出来的小分区。每个大分区有100个小分区，我们已经找出了每个小分区的前1000个数。将这100个分区的1000*100个数合并，找出每个大分区的前1000个数。

e、合并大分区。我们有1000个大分区，上一步已找出每个大分区的前1000个数。我们将这1000*1000个数合并，找出前1000.这1000个数就是所有数据中最大的1000个数。

（a、b、c为map阶段，d、e为reduce阶段）