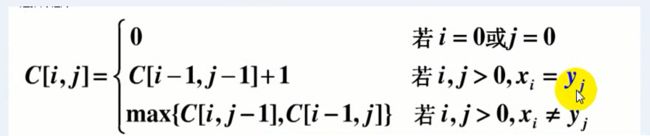java实现经典算法实例详解(递归,穷举,贪心,分治,动态规划,回溯,其他)求职必备
介绍一些经典算法,递归(二分法查找、欧几里得算法、汉诺塔、阶乘求解算法),穷举(泊松算法),贪心(背包),分治(循环赛日常表、棋盘问题),动态规划(最长公共子序列),回溯(八皇后),其他算法(约瑟夫杀人法)。
求职必须会的几类算法,建议可以用这几个例子做这几个算法的入门练习(已经写了很详细的解释),了解算法思想之后再刷题会好很多。
写在最前边:
递归,分治,归并等等这种按规律依次拆开,又依次合并,循环迭代的方式最开始那步都是等待变量变成1(递归的出口),也就是分到1个单位,然后再一一合并回去。
eg:
if (size == 1){
return;
}
1.递归
1.1汉诺塔
- 要把A最下边的那个盘子从A挪到C,要先把上边两个借助C挪到B;
- 然后把最下边那个大的从A挪到C;
- 再把剩下(目前在B上)的两个借助A挪到B(剩下两个的挪法,同上边挪动最大盘子的方法)。
代码实现:
package com.algorithm.recursion;
/**
* recursion:递归;
* 汉诺塔:递归
*/
public class HanNota {
private int i = 1;
public void hanNota(int n,char from,char dependOn,char to){
//n表示在挪第n个盘子;
if (n == 1){
//当只有一个盘子要挪动的时候,直接从from挪动到to;(表示的是被挪动柱子上最上边的一个盘子)
move(1,from,to);
}else{
hanNota(n-1, from, to, dependOn);//先将n-1个盘子从A利用C挪到B,n会一直减,直到n = 1,直接从from挪动到to
move(n, from, to); //将n这个盘子(底盘)从A挪到C;
hanNota(n-1, dependOn, from, to);//将n-1个盘子从B利用A挪到C;
}
}
private void move(int n, char from, char to) {
//移动过去之后直接打印作表示就可以;
System.out.println("第" + i++ +"步:第" + n +"个盘子从" + from + "------->" + to);
/* System.out.println("第" + i++ +"步从" + from + "------->" + to);*/
}
public static void main(String[] args){
HanNota hn = new HanNota();
hn.hanNota(3, 'A', 'B', 'C');
}
}
1.2欧几里德法求两个数的最大公约数
package com.algorithm.recursion;
/**
* 求一个数的最大公约数(简称:gcd)(欧几里德原理)
* (m>n)m和n的最大公约数 = n 和m%n的最大公约数
* eg: 36 和 24 12 24和36%24=12 12和24%12=0 则只剩余12;
*/
public class Gcd {
public int gcd(int m ,int n){
if (n == 0){
return m;
}else {
return gcd(n, m%n);
}
}
public static void main(String[] args){
Gcd test = new Gcd();
System.out.println(test.gcd(99, 11));
}
}
1.3二分法查找
代码:
package com.algorithm.recursion;
import com.sort.MergeSortSelf;
/**
* @author yn
* @description 二分法查找:递归的方式和非递归的方式;
*/
public class BinarySearchSelf {
/**
* 递归的方式
* @param elem
* @param array
* @param low
* @param high
* @return
*/
public int binarySearch(int elem,int[] array,int low,int high){
if (low>high){
return -1;
}
int middle = (low+high)/2;
if (array[middle] == elem){
System.out.println("找到这个元素的对应下标值为:" + middle);
return middle;
}
if (array[middle] < elem){
//找右边
return binarySearch(elem, array, middle+1, high);
}
if (array[middle] > elem){
//找左边
return binarySearch(elem, array, low, middle-1);
}
return -1;
}
/**
* 非递归的方式
* @param array
* @param elem
* @return
*/
public int directBinarySearch(int[] array,int elem){
int low = 0;
int high = array.length-1;
while (low <= high){
int middle = (low+high)/2;
if(elem>array[middle]){
//往右边找
low = middle+1;
}else if (elem1.4阶乘求解:
这个比较简单
package com.algorithm.recursion;
/**
* 递归求阶乘;
*/
public class CalNFact {
public int f(int n){
if (n ==1){
return n;
}
else{
return n*f(n-1);
}
}
public static void main(String[] args){
CalNFact test = new CalNFact();
System.out.println(test.f(5));
}
}
2.动态规划:
2.1 最长公共子序列:
package com.algorithm;
/**
* @author yn
* 最长公共子序列(LCS)问题
*/
public class LCS {
public int findLCS(String m,String n){
//x和y分别表示两个字符串的长度,根据各自的字符串长度构建二维数组;
int x = m.length();
int y = n.length();
char[] mm = m.toCharArray();
char[] nn = n.toCharArray();
int[][] dp = new int[x][y];
//第一行
for (int i=0;i附加几个动态规划的问题:
找零钱问题; 走方格问题;
走台阶问题(爬楼梯问题):
问题描述:
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
链接:https://leetcode-cn.com/articles/climbing-stairs/
- 方法1:暴力递归;
- 方法2:记忆性递归;
- 方法3:动态规划---->第三项等于前两项之和;
3.穷举法:
3.1泊松分酒:
package com.algorithm;
/**
* 泊松分酒(穷举法);三个酒瓶,目标盛酒量
* 制定一定的倒酒策略;
* 1-->2-->3-->1
*
*/
public class ShareWine {
private int b1 = 12;
private int b2 = 8;
private int b3 = 5;
private int m = 6; //目标酒量;
//假设一开始是12,0, 0
public void backBottle(int bb1,int bb2,int bb3){
System.out.println("bb1:" + bb1 + " bb2:" + bb2 + " bb3:" + bb3);
if (bb1 == m||bb2 == m||bb3 == m){
//当有任意一个瓶子的容量等于目标酒量的时候就算是找到了这个瓶子;
System.out.println("Find the bottle!");
return;
}
//先看瓶子2,分情况,瓶子2里边有酒,瓶子3里边的酒不等于自己的容量,说明瓶子3没有满;
if (bb2 != 0 && bb3 != b3){
//把瓶子2的酒倒入瓶子3,将瓶子3倒满;
//两种情况:把2里边的全部倒进3,3还没有满;3被倒满了,2中还有剩。
if (bb2+bb3= b2){
backBottle(bb1-b2, b2, bb3);
}else {
backBottle(0, bb1, bb3);
}
}
}
public static void main(String[] args){
ShareWine shareWine = new ShareWine();
shareWine.backBottle(12, 0, 0);
}
}
4.贪心算法:
4.1背包问题:
4.1.1.取价值最大;
贪心算法:背包问题;
- 求价值,先拿价值大的,先对价值进行排序;
- 性价比相同的时候,应该先拿质量大的,因为按比例计算,大的价值更大;
这个算法的写法没有拿到最优解;
代码:
package com.algorithm;
import java.util.Arrays;
/**
* 贪心算法:背包问题;
*
* 求价值,先拿价值大的,先对价值进行排序;
* 性价比相同的时候,应该先拿质量大的,因为按比例计算,大的价值更大;
* 这个算法的写法没有拿到最优解;
*/
public class GreedyPackage {
private int MAX_WEIGHT = 150;//背包最大容量;
private int[] weights = new int[]{35,30,60,50,40,10,25};
private int[] values = new int[]{10,40,30,50,35,40,30};
private void packageGreedy(int capacity,int[] weights,int[] values){
int n = weights.length;
double[] r = new double[n];//性价比数组;
int[] index = new int[n];//按性价比排序的 物品的下标;
for (int i=0;i r[i]){
temp = r[j];
r[j] = r[i];
r[i] = temp;
//性价比排完序之后,对应的物品的下标也要进行排序,才能使得性价比和对应物品下标一一对应;
int x = index[j];
index[j] = index[i];
index[i] = x;
}
}
}
//排序好的重量和价值分别存到数组;
int[] w1 = new int[n];
int[] v1 = new int[n];
for (int i=0;i 但是实际中情况很多
视频中的疑点:

如果 4对应的是16 那就选第二种情况;
特殊情况(如下):

视频中的解法没有拿到最优解,只是尽可能大的价值最大值
4.1.2.单一背包问题:
最终拿的物品的体积必须是背包的体积,不能多不能少;
5.分治算法:
5.1循环赛(体育赛事)日程安排(球赛):

其实就是矩阵的特殊排列,使用到了递归,
有点像归并,先递归分治,再一一返回合并填充(按照规律);
代码:
package com.algorithm;
/**
* 分治法:球赛的日程安排
* 中间也叠加了递归的思想;8分4,4分2,2分1;然后开始一一返回去;
*/
public class SportsSchedule {
public void sportsSchedule(int[][] table,int n){
if (n == 1){
//当n等于1的时候,也就是只有一支球队,二维table数组的[0][0]位置就只有一个1;
table[0][0] = 1;
}else{
//填充左上区域矩阵
int m = n/2;
sportsSchedule(table, m);
//填充右上区域矩阵;
for (int i=0;i5.2棋盘问题(L型,骨盘)
package com.algorithm;
/**
* 棋盘问题;
* L型矩阵
*/
public class ChessBoradProblem {
private int[][] board;//棋盘
private int specialRow;//特殊点的行下标;
private int specialCol;//特殊点的列下标;
private int size;
private int type = 0;
//添加构造方法;
public ChessBoradProblem(int specialRow, int specialCol, int size) {
super();
this.specialRow = specialRow;
this.specialCol = specialCol;
this.size = size;
board = new int[size][size];
}
/**
*
* @param speacialRow 特殊点的行下标
* @param specialCol 特殊点的列下标
* @param leftRow 矩阵的左边起点行下标
* @param leftCol 矩阵的左边起点列下标
* @param size 矩阵的宽或者高
*/
private void chessBorad(int speacialRow,int specialCol,int leftRow,int leftCol,int size){
if (size == 1){
return;
}
int subSize = size/2;
type = type%4 + 1;
int n = type;
//假设特殊点在左上角区域:
if (speacialRow < leftRow + subSize && specialCol < leftCol + subSize){
chessBorad(speacialRow, specialCol, leftRow, leftCol, subSize);
}else{
//不在左上角,左上角矩阵的右下角矩阵就是特殊点;??
board[leftRow+subSize-1][leftCol+subSize-1] = n;
chessBorad(leftRow+subSize-1, leftCol+subSize-1, leftRow, leftCol, subSize);
}
//假设特殊点在右上角区域:
if (speacialRow < leftRow + subSize && specialCol >= leftCol + subSize){
chessBorad(speacialRow, specialCol, leftRow, leftCol + subSize, subSize);
}else{
board[leftRow + subSize - 1][leftCol + subSize] = n;
chessBorad(leftRow + subSize - 1, leftCol + subSize, leftRow, leftCol + subSize, subSize);
}
//假设特殊点在左下角区域:
if (speacialRow >= leftRow + subSize && specialCol < leftCol + subSize){
chessBorad(speacialRow, specialCol, leftRow + subSize, leftCol, subSize);
}else{
board[leftRow + subSize][leftCol + subSize -1] = n;
chessBorad(leftRow + subSize, leftCol + subSize -1, leftRow + subSize, leftCol, subSize);
}
//假设特殊点在右下角区域:
if (speacialRow >= leftRow + subSize && specialCol >= leftCol + subSize){
chessBorad(speacialRow, specialCol, leftRow + subSize, leftCol + subSize, subSize);
}else{
board[leftRow + subSize][leftCol + subSize] = n;
chessBorad(leftRow + subSize, leftCol + subSize, leftRow + subSize, leftCol + subSize, subSize);
}
}
public static void main(String[] args){
int N =4;
int specialRow = 0;
int specialCol = 1;
ChessBoradProblem cbptest = new ChessBoradProblem(specialRow, specialCol, N);
cbptest.chessBorad(specialRow, specialCol, 0, 0, N);
cbptest.printChess();
}
private void printChess() {
for (int i =0;i6.回溯:
6.1 八皇后问题:
package com.algorithm;
/**
* @author yn
* @description 八皇后的问题
*/
public class Queen {
public static int num = 0;//累计方案;
public static final int MAXQUEEN = 8;
public static int[] cols = new int[MAXQUEEN];//定义cols数组,表示8列棋子皇后摆放的位置;
/**
* n 表示第n列的皇后,rows[]表示这列中那个位置不能放的标记;
* @param n 填第n列的皇后;
*/
public void getCount(int n){
boolean[] rows = new boolean[MAXQUEEN];//记录每列每个方格是否可以放皇后;
for (int m =0;m=0){
rows[cols[m] - d] = true;
}
//反斜方向
if (cols[m]+d<=(MAXQUEEN-1)){
rows[cols[m]+d] = true;
}
}
//到此知道了哪些位置不能放皇后;
for (int i = 0;i 7.其他
7.1约瑟夫杀人法
package com.algorithm;
/**
* @description: 约瑟夫杀人法
*/
public class JosephKill {
public static int n = 5;//一共n个人
public static int m = 3;//数到m就咔嚓一个人。
class Node{
int val;
Node next;
public Node(int val){
this.val = val;
}
}
public void killNode(){
Node header = new Node(1);//第一个节点;
Node x = header;//被点到的人;
for (int i=2;i这也是自己学习算法的一篇笔记,共勉,欢迎大家留言批评指正!