详解频分复用和正交频分复用及matlab实现

说明：最近看着多径衰落突然看到了频分复用，于是想着顺便把频分复用、时分复用搞搞清楚算了（码分复用暂时没看），于是乎又翻出了我的红宝书——樊大佬的《通信原理》，文中所说的课本均为该教材，书有多经典就不说了，还参考了几个博客大佬的博文，部分图来自于这些博客，这里主要是我自己的理解以及一些细节困惑的思考，是其他博客不会介绍的，顺便也用Matlab实现一下，还是自己亲自对着原理跑一跑程序更踏实一些。

该博文主要从以下几方面介绍：

1. 通信中信号的“复用”是什么以及为什么要复用？
2. 信号复用中的频分复用和时分复用的原理？
3. 详解频分复用以及matlab的实现。
4. 详解正交频分复用以及matlab的实现。
5. 频分复用与正交频分复用的优缺点与一些细节。

一、通信原理中的“复用”和复用的原因

在通信原理中，信号的复用主要是指信道被多路信号共享，原因是信道的传输能力比它要传输的信号的容量要高，所以可以允许有多个信号在该信道上传输，如同你在一个二十米宽的道路上只跑一辆汽车，资源多浪费，所以要让其他车辆共用该车道。

课本上给的概念：

复用是解决如何利用一条信道同时传输多路信号的技术。目的是为了充分利用信道的频带或时间资源，提高信道的利用率。

二、信号复用中的频分复用和时分复用

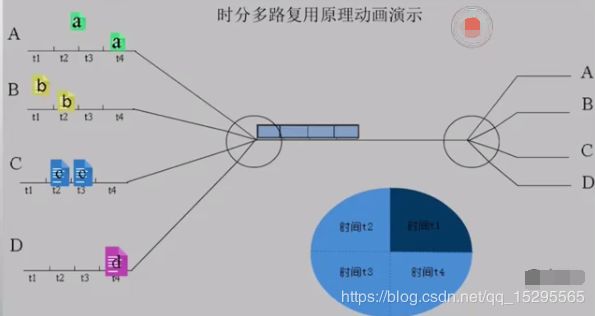
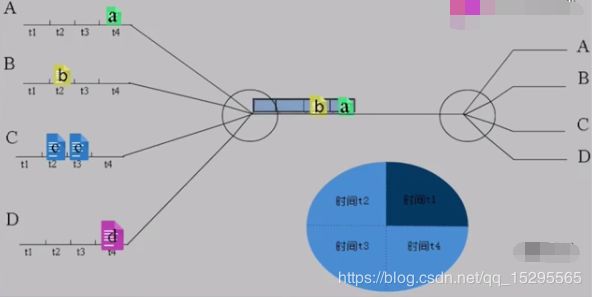
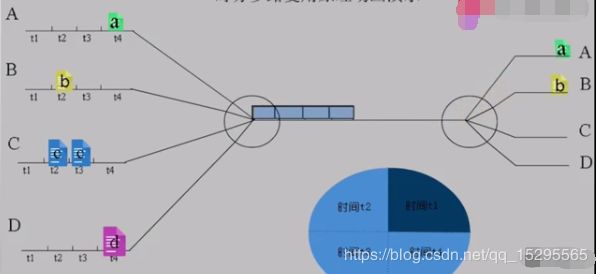
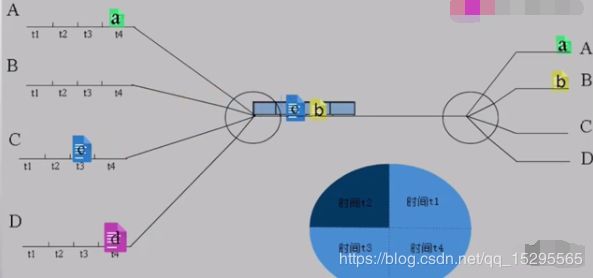
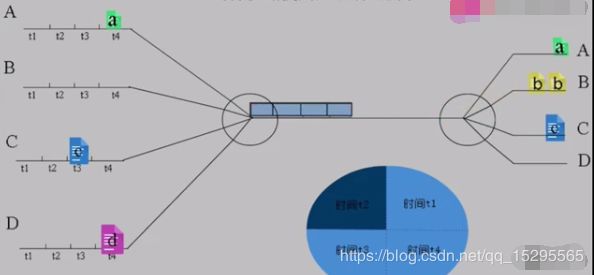
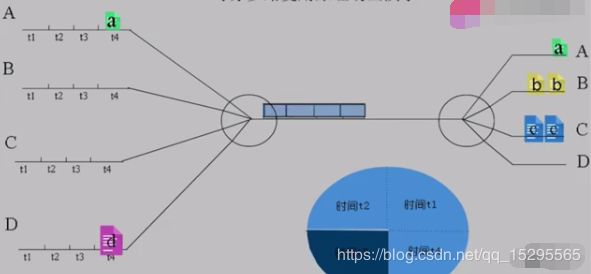
时分复用说白了是对时间的复用，以简单的单次复用为例，先看定义：

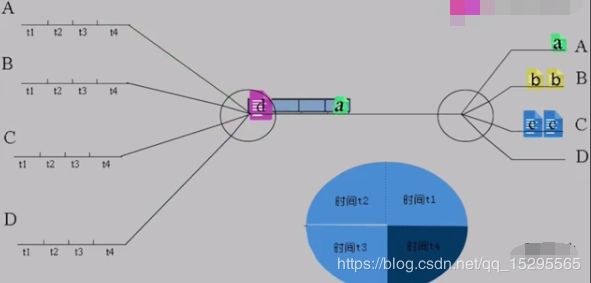
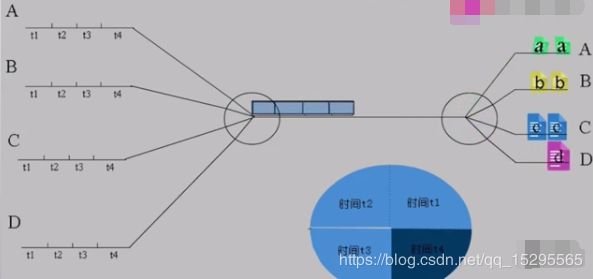
给整个信道传输信息的时间划分成若干时间片（简称时隙），并将这些时隙分配给每一个信号源使用，每一路信号在自己的时隙内独占信道进行数据传输。

举个形象的例子来说明：

蓝色方框中，t1+t2+t3+t4=T为一个周期。

初始位置

t1内，        

t2内，       

t3内，       

t4内，       

 

从图中可以看出时分复用就是在一个固定时间段内，将这段时间分成几段来进行数据传输。

频分复用

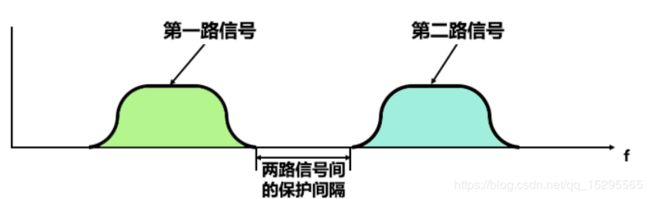
频分复用就是复用频率，类似于时分复用中的时间划分，所有数据传输都是在频域进行操作的，是将频率划分为了不同的频段，每个信号占用一个频段进行数据传输。用图表示如下图

这就是最简单的频分复用（FDM）示意图，中间有一定的频率间隔，使得两信号不会互相干扰。

那么我们会想，中间的保护间隔取多少为好，怎么取？这个稍后再介绍。

频分复用是一种按频率来划分信道的复用方式，在FDM中，信道的带宽被划分为多个不重叠的频段（子信道），没路信号占据其中一个子信道，并且各路之间必须留有未被使用的频带，进行隔离，以防止信号重叠。在接收端，使用适当的带通滤波器将多路信号分开，从而会付出所需要的信号。

三、详解频分复用以及matlab实现

频分复用主要用于模拟信号的多路传输（如多路载波电话系统以及调频立体声广播），也可以用于数字信号。

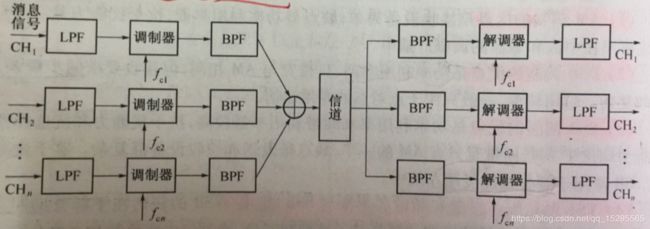
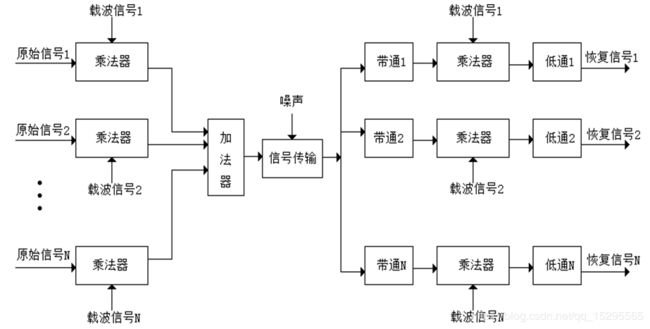
频分复用的系统原理图（来源于课本）为：

频分复用的系统原理图

在发送端，有LPF低通滤波器，调制器和BPF带通滤波器。

低通滤波器就是滤除高频信号，通过低频信号，所以我认为低通滤波器是用来限制所调制信号的最高频率。

调制器在这里就是一个乘法器，将调制信号与载波进行相乘，在频域为信号的卷积，所谓调制或者相乘的过程，在这里就是将低频的调制信号搬迁到载波所在的频率处，因此，频分复用的实质其实是信号的搬移。

带通滤波器在这里可有可无，主要是为了滤除搬移后信号中不需要的频率分量，只保留我们需要的信号。

然后将各路调制好的信号相加即可获得复用后的信号，通过信道进行传输。

在接收端，有带通滤波器，解调器和低通滤波器。

需要强调的是这里的带通滤波器是不同频率的滤波器，这些频率就是发送端载波频率，这里的带通滤波器是必须的，为了将各路不同的信号提取出来。

解调器与接收端的调制器一样，也是一个乘法器，也是与载波相乘，即对信号的解调。

低通滤波器也是必须的，主要是为了对解调后的信号进行基带信号的恢复，因为在相干解调过程中会有高频信号出现。

如果大家是电信人，那么对调制应该是很熟悉了，大类分为模拟调制和数字调制，调制信号和载波均为一维信号。在模拟调制中，分为常规幅度调制（AM），DSB（双边带调制），单边带调制（SSB），残留边带调制（VSB）和频率调制（FM）不同点主要在载波的幅值还是频率在随着调制信号变化（这里是从时域的角度来说，频谱搬迁是从频域角度来说）。

调制在通信过程中起着极其重要的作用：无线电通信是通过空间辐射方式传输信号的，调制过程可以将信号的频谱搬移到容易一电磁波形式辐射的较高频范围；此外，调制过程可以将不同的信号通过频谱搬移托付至不同频率的载波上，实现多路复用，不至于互相干扰。 

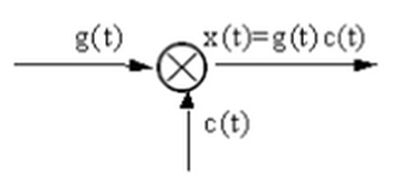
振幅调制是一种实用很广的连续波调制方式。调幅信号X(t)主要有调制信号和载波信号组成。调幅器原理如下图所示：

其中载波信号C(t)用于搭载有用信号，其频率较高。幅度调制信号g(t)含有有用信息，频率较低。

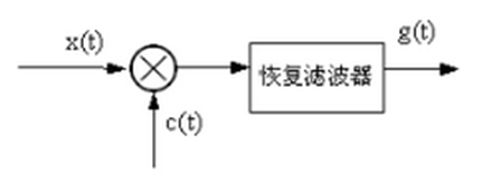
解调是调制的反过程。即：把低频信号从高频段搬移下来，还原被传送的低频信号。单边带解调不能采用包络检波，通常采用相干解调。解调器原理图为：

这里以两路信号为单边带调制SSB（为了节省一半的带宽），一路信号为调频FM的为例设计一个三路信号频分复用系统，应该怎么做？

为了简化模拟过程，不考虑噪声的存在，同时对频率进行特殊的设置，这样在发送端可以不需要低通和带通滤波器，需要设置的是：

1，三路调制信号均为正弦信号，信号频率设置为1khz,2khz,3khz。

2，两路SSB和一路FM的载波频率设置为10khz,20khz,30khz。

3，接收端带通滤波器和低通滤波器的设计。

简化后的框图为：

 滤波器选择切比雪夫带通和低通滤波器。

调制信号波和对应频谱图

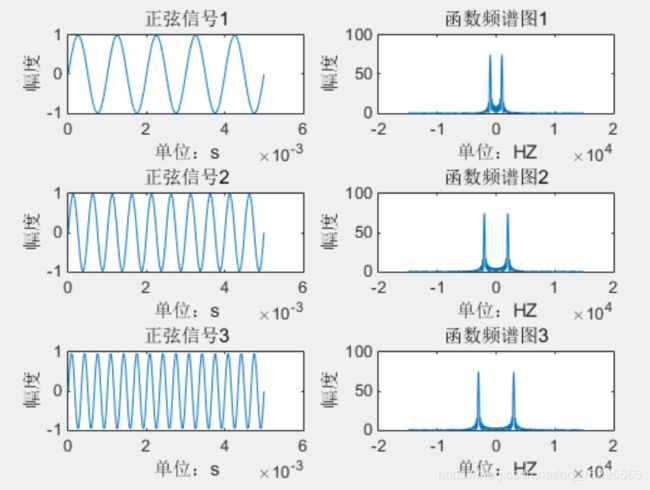
 调制信号的产生：

clc;
%%%正弦信号的产生
fs=30000;%采样频率
t=(0:1/fs:0.005);%图形坐标轴设计
f1=1000;f2=2000;f3=3000;%正弦信号频率
s1=sin(2*pi*f1*t);%产生正弦信号
s2=sin(2*pi*f2*t);
s3=sin(2*pi*f3*t);
figure(1)
subplot(3,2,1);plot(t,s1);xlabel('单位：s');ylabel('幅度');title('正弦信号1');%显示正弦信号图形
subplot(3,2,3);plot(t,s2);xlabel('单位：s');ylabel('幅度');title('正弦信号2');
subplot(3,2,5);plot(t,s3);xlabel('单位：s');ylabel('幅度');title('正弦信号3');
%%%频域分析
N=1024;
Y1=fft(s1,N);Y1=fftshift(Y1);%快速傅里叶变换得出频谱函数
Y2=fft(s2,N);Y2=fftshift(Y2);
Y3=fft(s3,N);Y3=fftshift(Y3);   
f=(0:N-1)*fs/N-fs/2;
subplot(3,2,2);plot(f,abs(Y1));xlabel('单位：HZ');ylabel('幅度');title('函数频谱图1');
subplot(3,2,4);plot(f,abs(Y2));xlabel('单位：HZ');ylabel('幅度');title('函数频谱图2');
subplot(3,2,6);plot(f,abs(Y3));xlabel('单位：HZ');ylabel('幅度');title('函数频谱图3');

 在matlab中，调制函数为modulate(x,fc,fs,'method')，x为调制信号，fc为载波频率（只需要知道载波频率即可），fs为采样频率（大于两倍的载波频率，即奈奎斯特采样定理），method为各种调制的方法，当然你也可以直接相乘来实现，这里我没有实现。

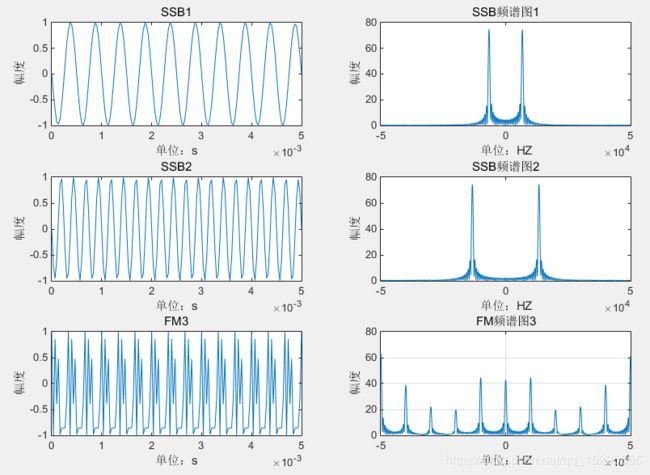
信号的调制显示及频谱图：

调制后的三路信号

matlab代码：

%%%SSB调制的频域分析
F1=fft(sm1,N);F1=fftshift(F1); 
F2=fft(sm2,N);F2=fftshift(F2);      
FM3=fft(sfm3,N);FM3=fftshift(FM3); 
f1=(0:N-1)*fs1/N-fs1/2;
subplot(3,2,2);plot(f1,abs(F1));xlabel('单位：HZ');ylabel('幅度');title('SSB频谱图1');
subplot(3,2,4);plot(f1,abs(F2));xlabel('单位：HZ');ylabel('幅度');title('SSB频谱图2');
subplot(3,2,6);plot(f1,abs(FM3));xlabel('单位：HZ');ylabel('幅度');title('FM频谱图3');
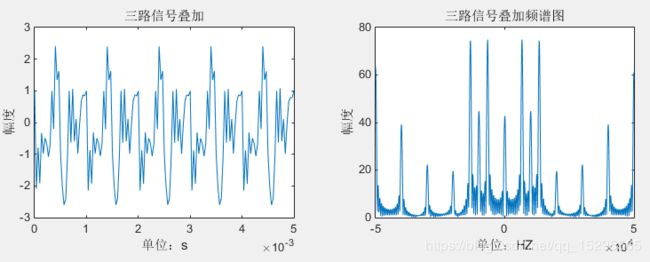
grid; 

把多个信号的频谱调制到不同的频带后，通过加法器将多个信号进行叠加。

三路信号叠加

%%%将三路信号叠加合成为一路在信道中传输%%%
dj1=sm1+sm2+sfm3;%三路信号叠加							
figure(3)	
subplot(2,2,1);plot(t,dj1);xlabel('单位：s');ylabel('幅度');title('三路信号叠加');
%%%三路信号叠加合成为一路信号的频谱分析
DJ1=fft(dj1,N);DJ1=fftshift(DJ1);   
subplot(2,2,2);plot(f1,abs(DJ1));xlabel('单位：HZ');ylabel('幅度');title('三路信号叠加频谱图');

解调过程：

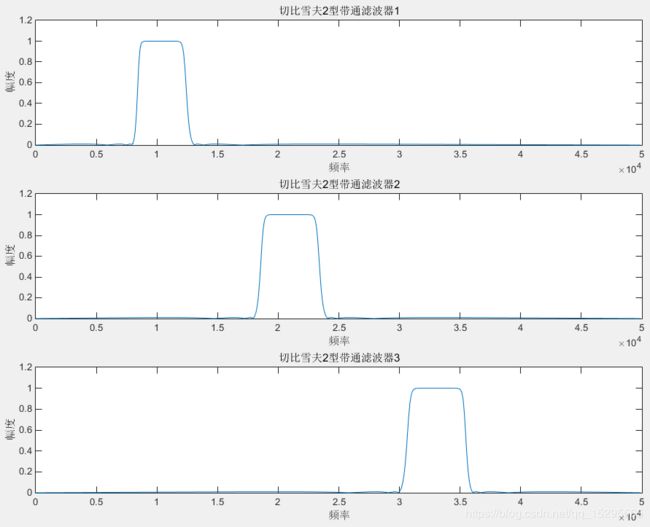
先设计带通滤波器，频谱图如下所示：

带通滤波器的频谱图

 带通滤波器matlab代码：

%%%带通滤波器的设计
fs1=100000;
Rp=0.5;Rs=40;  %用切比雪夫2型设计带通滤波器1；               
Wp1=[9000 12000]/50000;   %数字频率 fs1/2=50000         
Ws1=[8000 13000]/50000;
[n1,Wn1]=cheb2ord(Wp1,Ws1,Rp,Rs);
[b1,a1]=cheby2(n1,Rs,Wn1);
[h1,w1]=freqz(b1,a1);%显示切比雪夫2型设计带通滤波器频率响应
Wp2=[19000 23000]/50000;  %用切比雪夫2型设计带通滤波器2；    
Ws2=[18000 24000]/50000;
[n2,Wn2]=cheb2ord(Wp2,Ws2,Rp,Rs);
[b2,a2]=cheby2(n2,Rs,Wn2);
[h2,w2]=freqz(b2,a2);
Wp3=[31000 35000]/50000;  %用切比雪夫2型设计带通滤波器3；                          
Ws3=[30000 36000]/50000;
[n3,Wn3]=cheb2ord(Wp3,Ws3,Rp,Rs);
[b3,a3]=cheby2(n3,Rs,Wn3);
[h3,w3]=freqz(b3,a3);
figure(4);
subplot(3,1,1);plot(w1*fs1/(2*pi),abs(h1));xlabel('频率');ylabel('幅度');title('切比雪夫2型带通滤波器1');
subplot(3,1,2);plot(w2*fs1/(2*pi),abs(h2));xlabel('频率');ylabel('幅度');title('切比雪夫2型带通滤波器2');
subplot(3,1,3);plot(w3*fs1/(2*pi),abs(h3));xlabel('频率');ylabel('幅度');title('切比雪夫2型带通滤波器3');

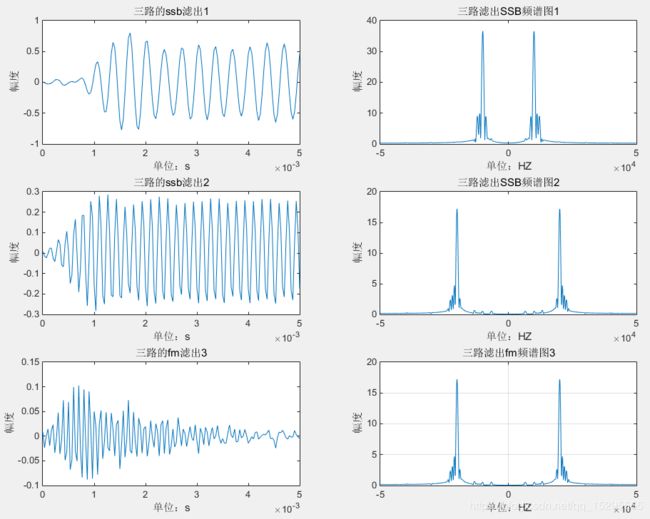
解调过程中使用带通滤波器进行滤波操作：

滤波后的波形图

滤波过程的matlab代码：

%不加噪声三路的滤出
lv11=filter(b1,a1,dj1);
lv12=filter(b2,a2,dj1);
lv13=filter(b3,a3,dj1);
figure(5)
subplot(3,2,1);plot(t,lv11);xlabel('单位：s');ylabel('幅度');title('三路的ssb滤出1');%图为滤出后3路信号各自的时域波形
subplot(3,2,3);plot(t,lv12);xlabel('单位：s');ylabel('幅度');title('三路的ssb滤出2');
subplot(3,2,5);plot(t,lv13);xlabel('单位：s');ylabel('幅度');title('三路的fm滤出3');
F11=fft(lv11,N);F11=fftshift(F11); 
F22=fft(lv12,N);F22=fftshift(F22);      
F33=fft(lv12,N);F33=fftshift(F33);
subplot(3,2,2);plot(f1,abs(F11));xlabel('单位：HZ');ylabel('幅度');title('三路滤出SSB频谱图1');
subplot(3,2,4);plot(f1,abs(F22));xlabel('单位：HZ');ylabel('幅度');title('三路滤出SSB频谱图2');
subplot(3,2,6);plot(f1,abs(F33));xlabel('单位：HZ');ylabel('幅度');title('三路滤出fm频谱图3');
grid;  

 通过解调器进行解调：

在matlab中，有对应的解调函数admeod函数，这里利用乘法器进行解调。

解调结果示意图

 解调的matlab代码：

%%%对不加噪声滤出的三路信号解调
s10=lv11.*cos(2*pi*10000*t/fs);	%各个已调信号分别乘以各自的高频载波信号
s20=lv12.*cos(2*pi*20000*t/fs);
s30=lv13.*cos(2*pi*30000*t/fs);
Z10=fft(s10,N);Z10=fftshift(Z10);  %解调信号频谱 
Z20=fft(s20,N);Z20=fftshift(Z20);  
Z30=fft(s30,N);Z30=fftshift(Z30);
figure(6)
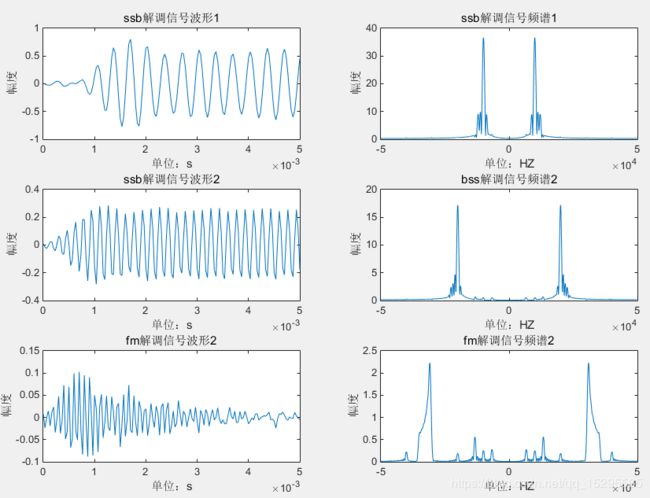
subplot(3,2,1);plot(t,s10);xlabel('单位：s');ylabel('幅度');title('ssb解调信号波形1')
subplot(3,2,2);plot(f1,abs(Z10));xlabel('单位：HZ');ylabel('幅度'); title('ssb解调信号频谱1') 
subplot(3,2,3);plot(t,s20);xlabel('单位：s');ylabel('幅度');title('ssb解调信号波形2')
subplot(3,2,4);plot(f1,abs(Z20));xlabel('单位：HZ');ylabel('幅度'); title('bss解调信号频谱2') 
subplot(3,2,5);plot(t,s30);xlabel('单位：s');ylabel('幅度');title('fm解调信号波形2')
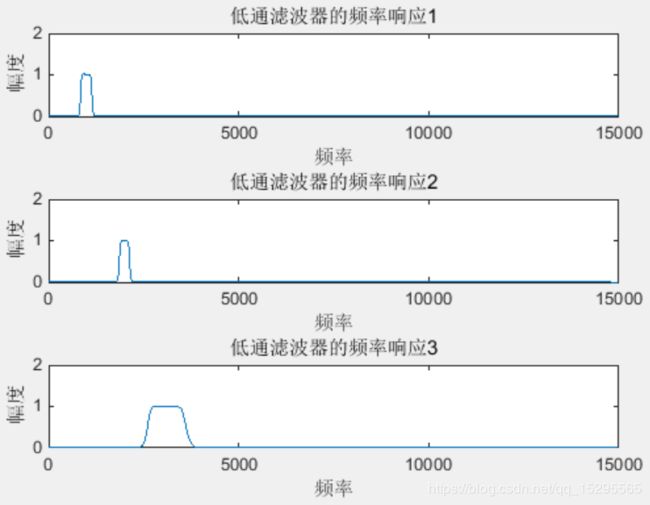
subplot(3,2,6);plot(f1,abs(Z30));xlabel('单位：HZ');ylabel('幅度'); title('fm解调信号频谱2') 

低通滤波器的设计图：

低通滤波器频谱图

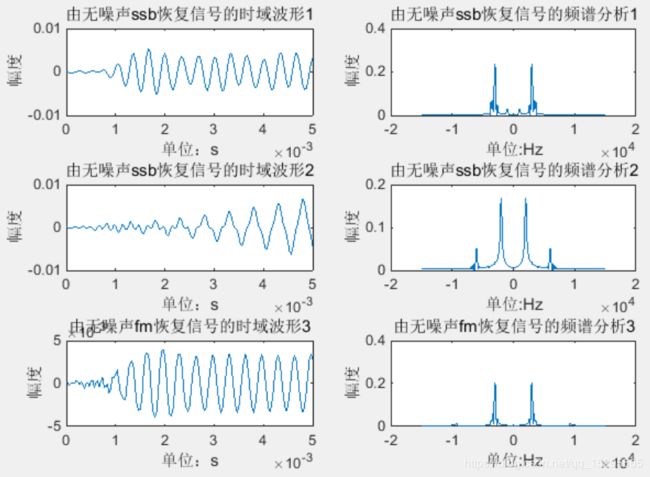
解调后经过低通滤波器的滤波后的图像示意图：

三路信号的恢复图以及频谱图

四、详解正交频分复用以及matlab的实现

（待写）

 

参考资料：

1，樊昌信《通信原理》

2，详解MATLAB/SIMULINK通信系统建模与仿真

3，博客 给"小白"图示讲解OFDM的原理

4，博客 用离散傅里叶变换来实现OFDM