CARRY4(超前快速进位逻辑结构)和多位比较器/加法器实现
先说一段废话
近期萌生了写技术博客的念头,一来是可以记录一些遇到的技术问题,理清思路,也可以记录自己的技术成长;二来是可以将自己的知识分享,以便后人再碰到时能从容不破。希望今后在碰到原创有价值的问题时能坚持这一习惯,也算是督促自己,下面进入正题。
问题的引出
这里有一个问题,一个32位的比较器需要使用多少个LUT。苦思冥想仍然未能得到答案,写程序后查看RTL网表,得到了答案。但是又看到了一个新的结构carry4(超前快速进位逻辑结构),这个结构会用在多位的比较器和多位的加法器上,要理解比较器和加法器的工作原理就需要理解这个超前快速进位逻辑。经过仔细研究,引出了这边文章。
这个结构可以查阅这篇文档:
https://www.xilinx.com/support/documentation/user_guides/ug474_7Series_CLB.pdf
讨论
首先给出答案一个32位的比较器需要使用32个LUT。具体这个超前快速进位逻辑结果起什么作用慢慢进行分析。
通过RTL网表可以看出,综合出来的结构如下图:

图中的小方块是LUT,有32个,稍大的是carry4结构,有4个。要理解这个RTL是如何实现32位的比较功能,就需要对这32个LUT和4个carry4分别进行分析。
1、32位比较器中的LUT
首先,32位比较器总共有64bit(位)输入,实现两32位数(a,b)比较,if(a>b)输出1;else 输出0;可以看到八个4输入LUT为一组,接到carry4结构中。这八个4输入LUT又分为两组,前四个一组,后四个一组。前四个实现a>b的比较,后四个实现a=b的比较。
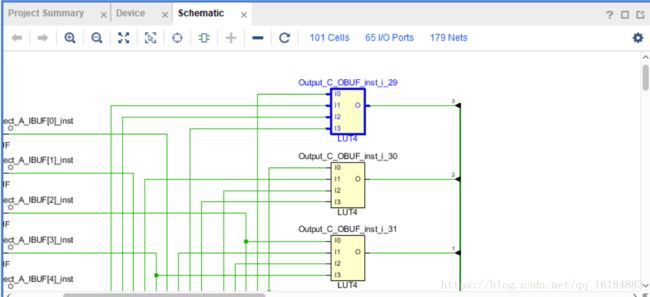
可以看到前四个LUT中的第一个为4输入,分别连接a和b的2bit。简化真值表如下:
| 输入 | 输出O |
|---|---|
| a>b | 1 |
| a=b | 0 |
a| 0 |
|
后四个同理,简化真值表如下:
| 输入 | 输出O |
|---|---|
| a>b | 0 |
| a=b | 1 |
a| 0 |
|
这样前四个LUT分别判断了a、b两数的0-1、2-3、4-5、6-7位的是否大于。后四个判断了是否等于。那么最简单的比较就是比较高两位了,如果高两位a[31:30]>b[31:30],那么就可以输出1了。
但是只这样比较是不全面的,如果高两位a不大于b,并不代表这a就小于或者等于b了,还需要比较后两位,再后两位这样循环下去,直至比较到最低两位,才能确定结果。
判断32位的数简单的流程来讲就是进行比较:如果高八位a大于b,那么肯定a大于b,输出1;如果高八位a小于或等于的话,输出是0。
但是仅仅是比较高8位是不全面的,高八位不大于的话有可能次八位还是a大,本应该输出1,却输出了0,这是不对的,所以就需要判断高八位是否等于,如果等于就继续判断后八位,循环下去。这也就是为什么每八bit需要八个LUT分别分为两组来判断大于、等于。就是为了如果高八位不大于的话,判断是等于,就会去判断后八位。这里就需要用到carry4结构来获取后八位的比较结果了。
同样的,我们讲的是一个lut负责两位,一组的前四个有四bit的输出,而不是1bit,如何把4bit的输出也联系起来,变成1bit,也需要这个carry4结构。
2、carry4的结构
这个carry4的结构如图,理解这个结构也可以参考论坛的这个帖子 :
https://blog.csdn.net/bbs165198646/article/details/76895919
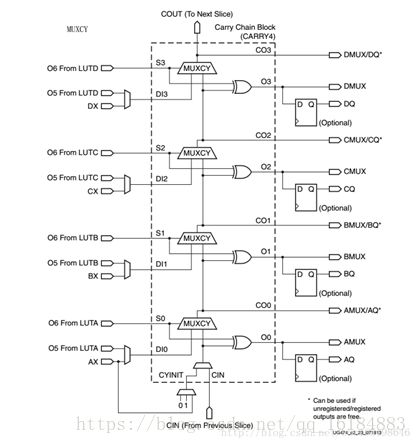
carry4的输出是DI/S/CIN,输出是CO/O/COUT(CO3)。
在上面可以看到八个LUT接到一个carry4上,接法是a>b的判断(前四个输出)作为DI0输入,a=b的判断(后四个输出)作为S0输入。CIN接下一级carry4的输出COUT,接法细节如图:
对工作流程进行分析:
如果最高位相等(S3=1),mux选择器就会选择下一级的选择器,如果不等(S3=0)mux选择器就会选择DI3,这样的话就实现了判断,并将八个一组LUT联系起来了。
- 只分析1bit,如果这一比特的值相等,则看低位bit的判断值/进位值;
- 如果这一比特的值不等,则输出值等于DI3,此时的输出值就确定了是大于,还是小于,而且不包括等于的情况。
- 如果高位等于,就输出就看低位的判断值,如果低位大于就输出1,小于就输出0,仍等于,则继续由下一级决定。
- 如果直到最下面的mux仍是等于,则由CIN决定输出值。
一个carry4的功能就如上,可以实现8bit的数的比较。而由于比较器是32位的,即四组LUT,就需要四个carry4。
继续上面的分析,当最下面的mux仍是等于,由CIN决定输出值。而CIN接到了下一级的COUT(CO3)上,串联起来,可以参考第一个图。
这样就将四组的比较值联系了起来,从最高两位比较到最低两位。如果最低两位仍然相等,那么输出值就由CYINT决定。由于比较器是if(a>b) 输出1,其他输出0,所以CYINT就是0,即两数相等。如果比较器是if(a>=b) 输出1,其他输出0,则CYINT就被设置为1。这里可以自己跑跑看,就可以比较出差别。
3、carry4用于多位加法器
对于多位的加法器实现,也会用到carry4,具体的分析在第二个链接里有,这里只贴图对一些细节进行一个补充说明。
a=4’b0101;
b=4’b0011;
S = a^b = 4’b0110;
对a和b做加法。
S输入的是a与b的异或值(异或就是不进位加法)。DI输入任何一个值(a或b)都可以。选择器在S等于0(前面的不相等)的时候选择DI,否则选择下一级CO。

如何实现加法,首先S就是异或结果,异或为:【00-0,10-1,01-1,11-0(未进位)】只是缺少进位的加法。
这里首先分析如何实现进位,也就是CO端口(1为进位,0为不进位)。
- 当S等于0时有两种情况,00或者11,此时选择器的选择由DI决定,00时输出0,也就进位是0;11时输出的是1,刚好是进位了。
- 当S等于1时有两种情况,01或者10,此时选择器的选择由CO,即下一级进行,也就是进位项进行,如果进位项是1,刚好加起来进位,如果是0则不进位。上面的情况分别为1234,继续分析
如何把值算对就靠的是C了。
- 当S为0时,与下一级进行异或(相同0;不同1),也就是说此时00或者11了,本位的情况由下一级的进位情况决定,下一级为0本位就是0,下一级为1本位就进一位为1.
- 当S为1时,与下一级异或,下一级为1时进位,本位为0 ,下一级为0时不进位,本位为1(单bit加法,进位由前面的搞定)。
最后加法结果是C(1000)正确值,进位情况是CO(0111)。
分析到这里就得感慨数字电路的奇妙,巧妙的利用选择器和异或逻辑就可以实现进位和加法的运算,通过多级级联进位,就可以实现多位的判断。
本文就到这里了,水平有限,有错误和提升的还请指正。
最后念一句诗,业精于勤而荒于嬉,希望自己能够坚持积累,坚持成长。