Python 气象数据分析 -- 《Python 数据分析实战》

选取了10个城市。随后将分析它们的天气数据，其中5个城市在距海100公里范围内，其余5个距海100～400公里。

选作样本的城市列表如下：
Ferrara（费拉拉）
Torino（都灵）
Mantova（曼托瓦）
Milano（米兰）
Ravenna（拉文纳）
Asti（阿斯蒂）
Bologna（博洛尼亚）
Piacenza（皮亚琴察）
Cesena（切塞纳）
Faenza（法恩莎）

数据来源：http://openweathermap.org/

---

1.温度数据分析
进行数据分析的目的是尝试解释是否能够评估海洋是怎样影响气温的，以及是否能够影响气温趋势，因此同时来看几个不同城市的气温趋势。这是检验分析方向是否正确的唯一方式。因此选择三个离海最近以及三个离海最远的城市。

import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from dateutil import parser
import pandas as pd
import numpy as np

df_ferrara = pd.read_csv('ferrara_270615.csv')
df_milano = pd.read_csv('milano_270615.csv')
df_mantova = pd.read_csv('mantova_270615.csv')
df_ravenna = pd.read_csv('ravenna_270615.csv')
df_torino = pd.read_csv('torino_270615.csv')
df_asti = pd.read_csv('asti_270615.csv')
df_bologna = pd.read_csv('bologna_270615.csv')
df_piacenza = pd.read_csv('piacenza_270615.csv')
df_cesena = pd.read_csv('cesena_270615.csv')
df_faenza = pd.read_csv('faenza_270615.csv')

# 读取城市气象数据
# 取出要分析的温度和日期数据
y1 = df_ravenna['temp']
x1 = df_ravenna['day']
y2 = df_faenza['temp']
x2 = df_faenza['day']
y3 = df_cesena['temp']
x3 = df_cesena['day']
y4 = df_milano['temp']
x4 = df_milano['day']
y5 = df_asti['temp']
x5 = df_asti['day']
y6 = df_torino['temp']
x6 = df_torino['day']

# 把日期数据转换成 datetime 的格式
day_ravenna = [parser.parse(x) for x in x1]
day_faenza = [parser.parse(x) for x in x2]
day_cesena = [parser.parse(x) for x in x3]
dat_milano = [parser.parse(x) for x in x4]
day_asti = [parser.parse(x) for x in x5]
day_torino = [parser.parse(x) for x in x6]

# 调用 subplot 函数, fig 是图像对象，ax 是坐标轴对象
fig, ax = plt.subplots()

# 调整x轴坐标刻度，使其旋转70度，方便查看
plt.xticks(rotation=70)

# 设定时间的格式
hours = mdates.DateFormatter('%H:%M')

# 设定X轴显示的格式
ax.xaxis.set_major_formatter(hours)

#这里需要画出三根线，所以需要三组参数
ax.plot(day_ravenna,y1,'r',day_faenza,y2,'r',day_cesena,y3,'r')
ax.plot(dat_milano,y4,'g',day_asti,y5,'g',day_torino,y6,'g')
#显示图像
fig

结果：

离海最近的三个城市的最高气温比离海最远的三个城市低不少，而最低气温看起来差别较小。

可以沿着这个方向做深入研究，收集10个城市的最高温和最低温，用线性图表示气温最值点和离海远近之间的关系。

#10个城市的最高温和最低温，用线性图表示气温最值点和离海远近之间的关系
#dist:城市距和海边距离列表
dist = [df_ravenna['dist'][0],
        df_cesena['dist'][0],
        df_faenza['dist'][0],
        df_ferrara['dist'][0],
        df_bologna['dist'][0],
        df_mantova['dist'][0],
        df_piacenza['dist'][0],
        df_milano['dist'][0],
        df_asti['dist'][0],
        df_torino['dist'][0]
        ]
#temp_max:存放每个城市最高温度的列表
#temp_min:存放每个城市最低温度的列表
temp_max = [df_ravenna['temp'].max(),
            df_cesena['temp'].max(),
            df_faenza['temp'].max(),
            df_ferrara['temp'].max(),
            df_bologna['temp'].max(),
            df_mantova['temp'].max(),
            df_piacenza['temp'].max(),
            df_milano['temp'].max(),
            df_asti['temp'].max(),
            df_torino['temp'].max()
            ]

temp_min = [df_ravenna['temp'].min(),
    df_cesena['temp'].min(),
    df_faenza['temp'].min(),
    df_ferrara['temp'].min(),
    df_bologna['temp'].min(),
    df_mantova['temp'].min(),
    df_piacenza['temp'].min(),
    df_milano['temp'].min(),
    df_asti['temp'].min(),
    df_torino['temp'].min()
]

#先把最高温画出来
fig, ax = plt.subplots()
ax.plot(dist,temp_max,'ro')
fig

#scikit-learn库的SVR方法
from sklearn.svm import SVR

# dist1是靠近海的城市集合，dist2是远离海洋的城市集合
dist1 = dist[0:5]
dist2 = dist[5:10]

# 改变列表的结构，dist1现在是5个列表的集合
# 之后我们会看到 numpy 中 reshape() 函数也有同样的作用
dist1 = [[x] for x in dist1]
dist2 = [[x] for x in dist2]
# temp_max1 是 dist1 中城市的对应最高温度
temp_max1 = temp_max[0:5]
# temp_max2 是 dist2 中城市的对应最高温度
temp_max2 = temp_max[5:10]

# 调用SVR函数，在参数中规定了使用线性的拟合函数
# 并且把 C 设为1000来尽量拟合数据（因为不需要精确预测不用担心过拟合）
svr_lin1 = SVR(kernel='linear', C=1e3)
svr_lin2 = SVR(kernel='linear', C=1e3)

# 加入数据，进行拟合
svr_lin1.fit(dist1, temp_max1)
svr_lin2.fit(dist2, temp_max2)

# 关于 reshape 函数请看代码后面的详细讨论
xp1 = np.arange(10,100,10).reshape((9,1))
xp2 = np.arange(50,400,50).reshape((7,1))
yp1 = svr_lin1.predict(xp1)
yp2 = svr_lin2.predict(xp2)


# 限制了 x 轴的取值范围
ax.set_xlim(0,400)

# 画出图像
ax.plot(xp1, yp1, c='b', label='Strong sea effect')
ax.plot(xp2, yp2, c='g', label='Light sea effect')
fig

print svr_lin1.coef_  #斜率
print svr_lin1.intercept_  # 截距
print svr_lin2.coef_
print svr_lin2.intercept_

结果：

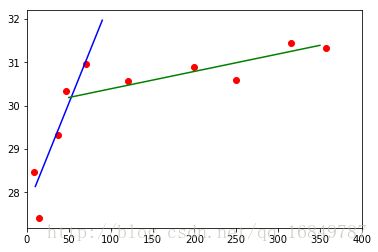
离海60公里以内，气温上升速度很快，从28度陡升至31度，随后增速渐趋缓和（如果还继续增长的话），更长的距离才会有小幅上升。这两种趋势可分别用两条直线来表示，直线的表达式为：x = ax + b
其中a为斜率，b为截距。
考虑将这两条直线的交点作为受海洋影响和不受海洋影响的区域的分界点，或者至少是海洋影响较弱的分界点。

#考虑将这两条直线的交点作为受海洋影响和不受海洋影响的区域的分界点，或者至少是海洋影响较弱的分界点
from scipy.optimize import fsolve

#定义第一条拟合直线
def line1(x):
    a1=svr_lin1.coef_[0][0]
    b1=svr_lin1.intercept_[0]
    return a1*x+b1

#定义第二条拟合直线
def line2(x):
    a2=svr_lin2.coef_[0][0]
    b2=svr_lin2.intercept_[0]
    return a2*x+b2

#定义了找到两条直线的交点的 x 坐标的函数
def findIntersection(fun1,fun2,x0):
    return fsolve(lambda x : fun1(x) - fun2(x),x0)

result=findIntersection(line1,line2,0.0)
print "[x,y]=[%d,%d]"%(result,line1(result))

fig, ax = plt.subplots()
x=np.linspace(0,300,31)
ax.plot(x,line1(x),x,line2(x),result,line1(result),'ro')
fig

结果：

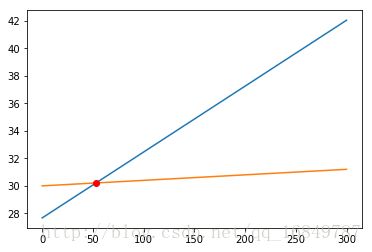
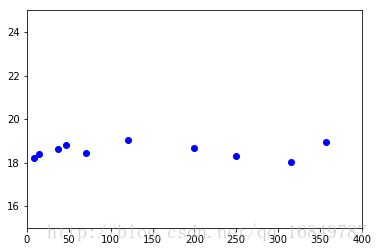
执行上述代码，将得到交点的坐标[x,y] = [ 53, 30 ]
因此，可以说海洋对气温产生影响的平均距离（该天的情况）为53公里。

现在，分析最低气温。

#最低温
fig, ax = plt.subplots()
plt.axis((0,400,15,25))
ax.plot(dist,temp_min,'bo')
fig

结果：

很明显夜间或早上6点左右的最低温与海洋无关

2.湿度数据分析
可以考察当天三个近海城市和三个内陆城市的湿度趋势。

import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from dateutil import parser
import pandas as pd
import numpy as np

df_ferrara = pd.read_csv('ferrara_270615.csv')
df_milano = pd.read_csv('milano_270615.csv')
df_mantova = pd.read_csv('mantova_270615.csv')
df_ravenna = pd.read_csv('ravenna_270615.csv')
df_torino = pd.read_csv('torino_270615.csv')
df_asti = pd.read_csv('asti_270615.csv')
df_bologna = pd.read_csv('bologna_270615.csv')
df_piacenza = pd.read_csv('piacenza_270615.csv')
df_cesena = pd.read_csv('cesena_270615.csv')
df_faenza = pd.read_csv('faenza_270615.csv')


# 读取城市湿度数据
# 取出要分析的湿度和日期数据
y1 = df_ravenna['humidity']
x1 = df_ravenna['day']
y2 = df_faenza['humidity']
x2 = df_faenza['day']
y3 = df_cesena['humidity']
x3 = df_cesena['day']
y4 = df_milano['humidity']
x4 = df_milano['day']
y5 = df_asti['humidity']
x5 = df_asti['day']
y6 = df_torino['humidity']
x6=df_torino['day']

# 把日期数据转换成 datetime 的格式
day_ravenna = [parser.parse(x) for x in x1]
day_faenza = [parser.parse(x) for x in x2]
day_cesena = [parser.parse(x) for x in x3]
dat_milano = [parser.parse(x) for x in x4]
day_asti = [parser.parse(x) for x in x5]
day_torino = [parser.parse(x) for x in x6]

# 调用 subplot 函数, fig 是图像对象，ax 是坐标轴对象
fig, ax = plt.subplots()

# 调整x轴坐标刻度，使其旋转70度，方便查看
plt.xticks(rotation=70)

# 设定时间的格式
hours = mdates.DateFormatter('%H:%M')

# 设定X轴显示的格式
ax.xaxis.set_major_formatter(hours)


#这里需要画出三根线，所以需要三组参数
ax.plot(day_ravenna,y1,'r',day_faenza,y2,'r',day_cesena,y3,'r')
ax.plot(dat_milano,y4,'g',day_asti,y5,'g',day_torino,y6,'g')
#显示图像
fig

结果：

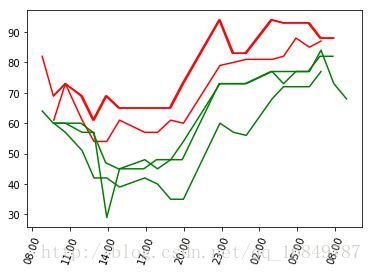
乍看上去好像近海城市的湿度要大于内陆城市，全天湿度差距在20%左右。再来看一下湿度的极值和离海远近之间的关系

#dist:城市距和海边距离列表
dist = [df_ravenna['dist'][0],
        df_cesena['dist'][0],
        df_faenza['dist'][0],
        df_ferrara['dist'][0],
        df_bologna['dist'][0],
        df_mantova['dist'][0],
        df_piacenza['dist'][0],
        df_milano['dist'][0],
        df_asti['dist'][0],
        df_torino['dist'][0]
        ]
# 获取最大湿度数据
hum_max = [df_ravenna['humidity'].max(),
df_cesena['humidity'].max(),
df_faenza['humidity'].max(),
df_ferrara['humidity'].max(),
df_bologna['humidity'].max(),
df_mantova['humidity'].max(),
df_piacenza['humidity'].max(),
df_milano['humidity'].max(),
df_asti['humidity'].max(),
df_torino['humidity'].max()
]

fig, ax = plt.subplots()
plt.plot(dist,hum_max,'bo')

# 获取最小湿度
hum_min = [df_ravenna['humidity'].min(),
df_cesena['humidity'].min(),
df_faenza['humidity'].min(),
df_ferrara['humidity'].min(),
df_bologna['humidity'].min(),
df_mantova['humidity'].min(),
df_piacenza['humidity'].min(),
df_milano['humidity'].min(),
df_asti['humidity'].min(),
df_torino['humidity'].min()
]
#fig, ax = plt.subplots()
plt.plot(dist,hum_min,'ro')

结果：

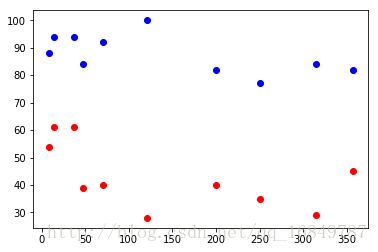
近海城市无论是最大还是最小湿度都要高于内陆城市。然而，还不能说湿度和距离之间存在线性关系或者其他能用曲线表示的关系。采集的数据点数量（10）太少，不足以描述这类趋势。

3.风向频率玫瑰图
在采集的每个城市的气象数据中，下面两个与风有关：
风力（风向） 风速

分析存放每个城市气象数据的DataFrame就会发现，风速不仅跟一天的时间段相关联，还与一个介于0~360度的方向有关。例如，每一条测量数据也包含风吹来的方向
为了更好地分析这类数据，有必要将其做成可视化形式，但是对于风力数据，将其制作成使用笛卡儿坐标系的线性图不再是最佳选择。

要是把一个DataFrame中的数据点做成散点图

#散点图不直观，给个例子
fig, ax = plt.subplots()
plt.plot(df_ravenna['wind_deg'],df_ravenna['wind_speed'],'ro')
#fig
plt.show()

结果：

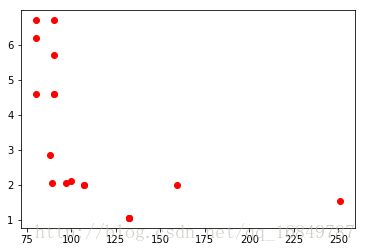
要表示呈360度分布的数据点，最好使用另一种可视化方法：极区图。

首先，创建一个直方图，也就是将360度分为八个面元，每个面元为45度，把所有的数据点分到这八个面元中。

#表示呈360度分布的数据点，使用另一种可视化方法：极区图
#360°八等份，分为八个面元，每份45°，把所有的数据点分到这八个面元中
#histogram()函数返回结果中的数组hist为落在每个面元的数据点数量。
[ 0 5 11 1 0 1 0 0]
#返回结果中的数组bins定义了360度范围内各面元的边界。
[ 0. 45. 90. 135. 180. 225. 270. 315. 360.]

hist,bins=np.histogram(df_ravenna['wind_deg'],8,[0,360])
print hist
print bins

histogram()函数返回结果中的数组hist为落在每个面元的数据点数量。

[ 0 5 11 1 0 1 0 0]

返回结果中的数组bins定义了360度范围内各面元的边界。

[ 0. 45. 90. 135. 180. 225. 270. 315. 360.]

要想正确定义极区图，离不开这两个数组。创建一个函数来绘制极区图，把这个函数定义为showRoseWind()，它有三个参数：
values数组，指的是想为其作图的数据，也就是这里的hist数组；
第二个参数city_name为字符串类型，指定图表标题所用的城市名称；
最后一个参数max_value为整型，指定最大的蓝色值。

def showRoseWind(values,city_name,max_value):
    N = 8

    # theta = [pi*1/4, pi*2/4, pi*3/4, ..., pi*2]
    theta = np.arange(0.,2 * np.pi, 2 * np.pi / N)
    radii = np.array(values)
    fig,ax=plt.subplots()
    # 绘制极区图的坐标系
    plt.axes([0.025, 0.025, 0.95, 0.95], polar=True)

    # 列表中包含的是每一个扇区的 rgb 值，x越大，对应的color越接近蓝色
    colors = [(1-x/max_value, 1-x/max_value, 0.75) for x in radii]

    # 画出每个扇区
    plt.bar(theta, radii, width=(2*np.pi/N), bottom=0.0, color=colors)

    # 设置极区图的标题
    plt.title(city_name, x=0.2, fontsize=20)
    fig

需要修改变量colors存储的颜色表。这里，扇形的颜色越接近蓝色，值越大。定义好函数之后，调用它即可：

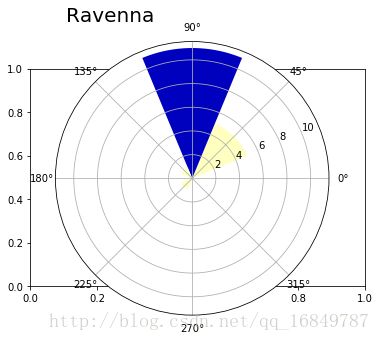
showRoseWind(hist,'Ravenna',max(hist))

结果：

整个360度的范围被分成八个区域（面元），每个区域弧长为45度，此外每个区域还有一列呈放射状排列的刻度值。在每个区域中，用半径长度可以改变的扇形表示一个数值，半径越长，扇形所表示的数值就越大。为了增强图表的可读性，我们使用与扇形半径相对应的颜色表。半径越长，扇形跨度越大，颜色越接近于深蓝色。

从刚得到的极区图可以得知风向在极坐标系中的分布方式。该图表示这一天大部分时间风都

吹向西南和正西方向。

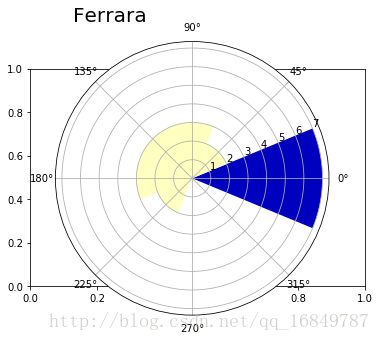
定义好showRoseWind()函数之后，查看其他城市的风向情况也非常简单。

#其他城市
hist, bin = np.histogram(df_ferrara['wind_deg'],8,[0,360])
print hist
showRoseWind(hist,'Ferrara', max(hist))
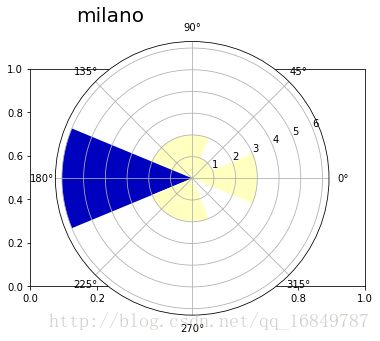
hist, bin = np.histogram(df_milano['wind_deg'],8,[0,360])
print hist
showRoseWind(hist,'milano', max(hist))

结果：


计算风速均值的分布情况

即使是跟风速相关的其他数据，也可以用极区图来表示。

定义RoseWind_Speed函数，计算将360度范围划分成的八个面元中每个面元的平均风速。

#计算风速均值的分布情况
def RoseWind_Speed(df_city):
    degs=np.arange(45,361,45)
    tmp=[]
    for deg in degs:
        #获取wind_deg在指定范围的平均风速
        #获取的是风向大于 'deg-46' 度和风向小于 'deg' 的数据。
        tmp.append(df_city[(df_city['wind_deg']>(deg-46)) & (df_city['wind_deg']'wind_speed'].mean())
    return np.array[tmp]

RoseWind_Speed() 函数返回一个包含八个平均风速值的NumPy数组。该数组将作为先前定义的showRoseWind()函数的第一个参数，这个函数是用来绘制极区图的。

hist,bins=np.histogram(df_ravenna['wind_deg'],8,[0,360])
print hist
print bins
showRoseWind(RoseWind_Speed(df_ravenna),'Ravenna',max(hist))