ResNet理论基础与具体实现（详细教程）

论文地址：Deep Residual Learning for Image Recognition

​ Identity Mappings in Deep Residual Networks

pytroch源码地址：resnet

0x00 前言

ResNet是2015年就提出的网络结构，中文名字叫作深度残差网络，主要作用是图像分类。现在在图像分割、目标检测等领域都有很广泛的运用，另外值得一提的是Alpha Zero中也使用了这种网络。

我第一次看到这个网络时的第一映像就是 这不就是一个差分放大电路吗？（由于本人是学电路出生）后来我得知Kaiming He原先是学数学的，这就让我感觉很困惑了。可能这种种的问题，最后都是殊途同归吧！！！

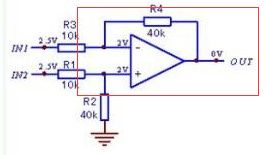
我想如果各位读完全文的话，也会和我有一样的看法吧？

0x01 问题的引出

随着硬件的不断升级，我们可以使得原来很浅的网络不断的加深，但是这种做法随之而来就出现了这样的一个问题深层训练的效果反而不如浅层网络，也就是网络出现了退化。这个问题很大程度上归结为网络层数过深，梯度下降优化loss变得困难。

作者为了解决上述问题，提出了这样一个结构：

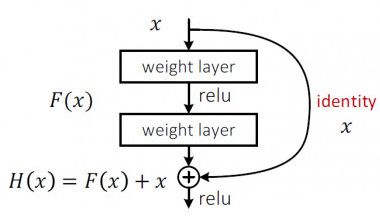
是不是和我前面提到的差分放大电路很像？

0x02 解决退化问题

如上图所示，作者添加了一个identity结构，也就是将输入x和卷积后的输出F(x)相加。如果我们要学习的目标函数是H(x)的话。

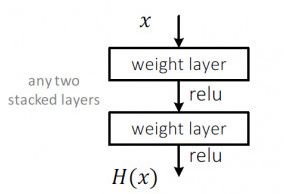
当需要拟合的函数H(x)很复杂的时候，H(x)和F(x)=H(x)-x近似等价，那么我们之前的学习目标H(x)就可以变成F(x)+x。为什么要这样的的做替换？因为F(x)的优化会比H(x)简单。为什么呢？这实际上是源自**残差表示法（Residual Representations）**的思想。

• 在图像识别中，VLAD是一种由残差向量关于字典的编码表示，而Fisher Vector可以被定义为VLAD的概率版本，它们都是图像检索和分类的强大的浅层表示。对于向量化，编码残差向量比编码原始向量更有效。
• 在低层次的视觉和计算机图形学中，为了解偏微分方程，一般使用的多网格法。就是将系统重新设计成多个尺度下的子问题，每个子问题负责一个较粗的和更细的尺度之间的残差解。多网格的另一种选择是分层基础的预处理，它依赖于在两个尺度之间表示残差向量的变量。研究表明，这些（转化成多个不同尺度的子问题，求残差解的）解决方案的收敛速度远远快于那些不知道残差的标准解决方案。

我们把$H(x)=F(x)+x$写成$y_l=h(x_l)+F(x_l,W_l)$，$x_{l+1}=f(y_l)$（$f$是激活函数）

那么如果$h(x_l)=x_l$和$f(y_l)=y_l$是恒等映射，那么上述公式表达为

• $x_{l+1}=x_l+F(x_l,W_l)$

通过网络的层数增加，我们不断增加residual block，最后得到的递归公式就是：

• $x_L=x_l+{\sum }_{i=l}^{L-1}F(x_i,W_i)$（L表示任意深的residual block）

而对于反向传播，假设损失函数是$\theta$，那么可以得到

• $\frac{\partial \theta }{\partial x_l}=\frac{\partial \theta }{\partial x_L}\frac{\partial \theta }{\partial x_l}=\frac{\partial \theta }{\partial x_L}(1+\frac{\partial }{\partial x_L}{\sum }_{i=l}^{L-1}F(x_i,W_i))$

我们可以看到整个式子分成了$\frac{\partial \theta }{\partial x_L}$和$\frac{\partial }{\partial x_L}{\sum }_{i=l}^{L-1}F(x_i,W_i)$两个部分。第一部分直接把深层的梯度传递到任意浅层，而第二项不可能为-1，所以这样的话浅层的梯度就不会消失。

0x03 residual block

整个网络最重要的部分就是上面的identity，我们称这个结构整体是residual block。现在我们要考虑的问题就是上述结构中，卷积层如何存放？激活函数如何存放？。。。这些问题。为此，作者对于不同方式做了比较

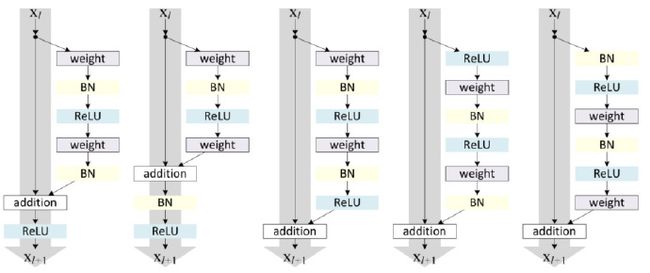
实验结果发现，最后一种方式的residual block效果最好。

这应该是早期residual block的模样，而由于技术的不断发展，后来出现了batch normalization这样的技术，residual block也做了相对应的调整，变成了现在的模样。

对于resnet18和resnet34

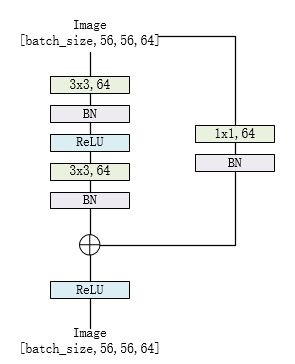
def conv3x3(in_planes, out_planes, stride=1):
    """3x3 convolution with padding"""
    return nn.Conv2d(in_planes, out_planes, kernel_size=3, stride=stride,
                     padding=1, bias=False)

class BasicBlock(nn.Module):
    expansion = 1

    def __init__(self, inplanes, planes, stride=1, downsample=None):
        super(BasicBlock, self).__init__()
        self.conv1 = conv3x3(inplanes, planes, stride)
        self.bn1 = nn.BatchNorm2d(planes)
        self.relu = nn.ReLU(inplace=True)
        self.conv2 = conv3x3(planes, planes)
        self.bn2 = nn.BatchNorm2d(planes)
        self.downsample = downsample
        self.stride = stride

    def forward(self, x):
        residual = x

        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)

        out = self.conv2(out)
        out = self.bn2(out)

        if self.downsample is not None:
            residual = self.downsample(x)

        out += residual
        out = self.relu(out)

        return out

对于resnet50、resnet101和resnet152

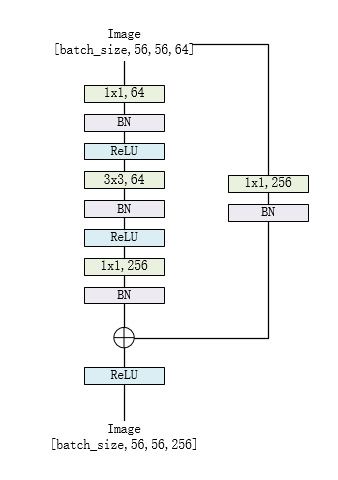
class Bottleneck(nn.Module):
    expansion = 4

    def __init__(self, inplanes, planes, stride=1, downsample=None):
        super(Bottleneck, self).__init__()
        self.conv1 = nn.Conv2d(inplanes, planes, kernel_size=1, bias=False)
        self.bn1 = nn.BatchNorm2d(planes)
        self.conv2 = nn.Conv2d(planes, planes, kernel_size=3, stride=stride,
                               padding=1, bias=False)
        self.bn2 = nn.BatchNorm2d(planes)
        self.conv3 = nn.Conv2d(planes, planes * 4, kernel_size=1, bias=False)
        self.bn3 = nn.BatchNorm2d(planes * 4)
        self.relu = nn.ReLU(inplace=True)
        self.downsample = downsample
        self.stride = stride

    def forward(self, x):
        residual = x

        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)

        out = self.conv2(out)
        out = self.bn2(out)
        out = self.relu(out)

        out = self.conv3(out)
        out = self.bn3(out)

        if self.downsample is not None:
            residual = self.downsample(x)

        out += residual
        out = self.relu(out)

        return out

0x04 网络结构

整体的resnet系列网络如下：

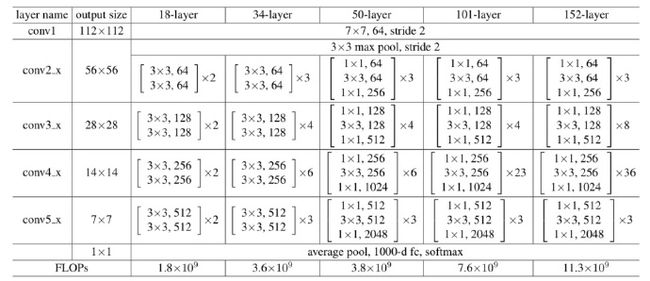
class ResNet(nn.Module):

    def __init__(self, block, layers, num_classes=1000):
        self.inplanes = 64
        super(ResNet, self).__init__()
        self.conv1 = nn.Conv2d(3, 64, kernel_size=7, stride=2, padding=3,
                               bias=False)#7x7,64
        self.bn1 = nn.BatchNorm2d(64)
        self.relu = nn.ReLU(inplace=True)
        self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)#maxpool
        self.layer1 = self._make_layer(block, 64, layers[0])
        self.layer2 = self._make_layer(block, 128, layers[1], stride=2)
        self.layer3 = self._make_layer(block, 256, layers[2], stride=2)
        self.layer4 = self._make_layer(block, 512, layers[3], stride=2)
        self.avgpool = nn.AvgPool2d(7, stride=1)#average pool
        self.fc = nn.Linear(512 * block.expansion, num_classes)

        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                n = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
                m.weight.data.normal_(0, math.sqrt(2. / n))
            elif isinstance(m, nn.BatchNorm2d):
                m.weight.data.fill_(1)
                m.bias.data.zero_()

    def _make_layer(self, block, planes, blocks, stride=1):
        downsample = None
        if stride != 1 or self.inplanes != planes * block.expansion:
            downsample = nn.Sequential(
                nn.Conv2d(self.inplanes, planes * block.expansion,
                          kernel_size=1, stride=stride, bias=False),
                nn.BatchNorm2d(planes * block.expansion),
            )

        layers = []
        layers.append(block(self.inplanes, planes, stride, downsample))
        self.inplanes = planes * block.expansion
        for i in range(1, blocks):
            layers.append(block(self.inplanes, planes))

        return nn.Sequential(*layers)

    def forward(self, x):
        x = self.conv1(x)
        x = self.bn1(x)
        x = self.relu(x)
        x = self.maxpool(x)

        x = self.layer1(x)
        x = self.layer2(x)
        x = self.layer3(x)
        x = self.layer4(x)

        x = self.avgpool(x)
        x = x.view(x.size(0), -1)
        x = self.fc(x)

        return x

代码和网络结构都是对应的，很容易理解。

关于网络结构我这里只举两个例子resnet18以及resnet50

def resnet18(pretrained=False, **kwargs):
    """Constructs a ResNet-18 model.

    Args:
        pretrained (bool): If True, returns a model pre-trained on ImageNet
    """
    model = ResNet(BasicBlock, [2, 2, 2, 2], **kwargs)#对应图中的2x2x2x2
    if pretrained:
        model.load_state_dict(model_zoo.load_url(model_urls['resnet18']))
    return model

def resnet50(pretrained=False, **kwargs):
    """Constructs a ResNet-50 model.

    Args:
        pretrained (bool): If True, returns a model pre-trained on ImageNet
    """
    model = ResNet(Bottleneck, [3, 4, 6, 3], **kwargs)#对应图中的3x4x6x3
    if pretrained:
        model.load_state_dict(model_zoo.load_url(model_urls['resnet50']))
    return model

这个代码的逻辑非常清晰，非常值得学习！！！

如有任何问题，希望大家指出！！！

reference:

https://blog.csdn.net/xxy0118/article/details/78324256