CVPR2010跟踪算法MOSSE原理及代码解析

文章和代码下载地址：

MOSSE: David S. Bolme, J. Ross Beveridge, Bruce A. Draper, Yui Man Lui. "Visual Object Tracking using Adaptive Correlation Filters." 

https://github.com/xingqing45678/Mosse_CF（代码和文章都在里面）

看了网上很多文章，大都是说“两个信号越相似，其相关值越高。在跟踪，就是找到与跟踪目标响应最大的项。”然后将相关的公式摆出来，看得我一头雾水，可能是我自己的基础不太好吧，最后查了很多资料，总算感觉自己有点明白了，所以将其记录下来，如果有不对的地方请指正。

一、对2D相关的理解

首先，相关是相关，卷积是卷积，不要混为一谈！！！！

互相关是用来度量两个信号在某个时刻的相似程度，对于机器视觉领域来说就是指两个图像patch的互相匹配的程度。

1、相关操作

图像的相关公式：，其中称为相关核(Kernel)，具体到每一个像素表示为：

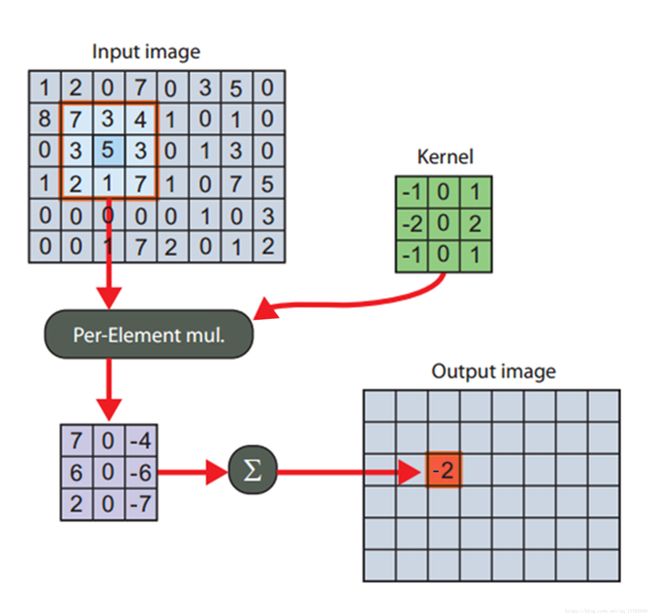
注：此图为网上转载 ，如图所示，Input Image为输入的图像。Kernel为相关核 ，也可以称作我们提前训练好的滤波器模板。Output image即为输出响应图像。

步骤：

      （1）滑动核，使其中心位于输入图像的像素上

      （2）利用上式求和，得到输出图像的像素值

     （3） 充分上面操纵，直到求出输出图像的所有像素值

例：计算输出图像像素值为

 

2、卷积操作

图像的卷积公式：，其中称为卷积核(Kernel)，具体到每一个像素表示为：

注：此图为网上转载（然后我p了一下） ，如图所示，Input Image为输入的图像。Kernel为相关核 ，也可以称作我们提前训练好的滤波器模板。Output image即为输出响应图像。 

步骤：

      （1）将卷积核围绕中心旋转180度

      （2）滑动核，使其中心位于输入图像的像素上

      （3）利用上式求和，得到输出图像的像素值

      （4）充分上面操纵，直到求出输出图像的所有像素值

例：计算输出图像像素值为

 

3、差异：

（1）引用专业术语就是：Two-dimensional correlation is equivalent to two-dimensional convolution with the filter matrix rotated 180 degrees.

白话：卷积将核旋转了180度。

（2）物理意义：相关可以反应两个信号相似程度，卷积不可以。

（3）卷积满足交换律，，相关不可以。

（4）卷积可以直接通过卷积定理（时域上的卷积等于频域上的乘积）来加速运算，相关不可以。

 

二、对相关滤波跟踪器的理解

相关滤波跟踪器就是通过互相关(cross-correlation)来定位目标当前帧所在位置的。响应图最大值对应的位置即为当前时刻预测的目标位置，具体流程如下：

如果我们在时域内求解响应图，运算量巨大，那么如何利用卷积定理将其转换到频域？？？

用卷积来表示相关就是：

利用卷积定理转换到频域为：

简写为：

其中，，表示点乘。所以将我们的输入图像和滤波器通过算法变换到频域后，直接将他们相乘，然后再变换回时域（也就是图像的空域）就可以得到响应图。

几点重要的解释：

（1）输入的图像是指目标检测区域（MOSSE的检测区域就是目标所在区域），可能是像素值也可能是提取的特征（eg.Hog，CN，DeepFeatures等）。

（2）滤波器（或者叫目标模板）的大小和检测区域的大小一样。因为相同大小的矩阵在频率域才可以点乘计算。

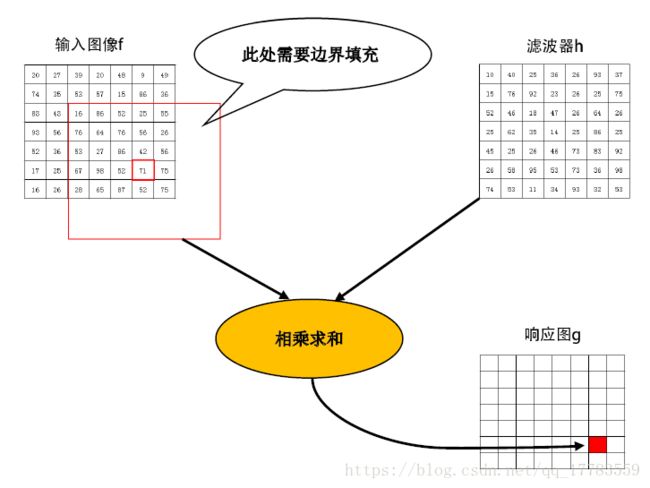
（3）当滤波器稍微偏移就会超出输入图像的范围，则需要填充数据（这就是卷积的边界效应）。然而在实际的相关滤波跟踪算法中，因为代码中直接就写频域的计算公式，所以我们不知道是如何填充边界的。常用的有三种填充方法，补零、补边界像素、循环图像，matlab中fft默认的是第三种。

三、对MOSSE的理解

经过上面的解释，应该都能明白相关滤波的检测原理，响应图峰值的位置即为当前帧目标的预测位置。为了得到响应图，那么我们求出滤波器模板频域的表示值即可：

1、预处理（不重要，一般都会进行这些操作）

（1）FFT卷积算法需要将图像和滤波器映射到拓扑结构上，边界采用循环图像的方式填充，即将图像的左边缘连接到右侧边缘，将顶部连接到底部。这就是上面所说的第三种填充方法。

（2）周期卷积会对输入数据进行周期填补，引入一些artifacts。作者通过如下如下论文中的方法减弱对输出响应的影响D. S. Bolme, B. A. Draper, and J. R. Beveridge. Average of synthetic exact filters. In CVPR, 2009. 2, 3。（具体细节可以不用深究）

（3）采用点乘余弦窗处理，使图像边缘慢慢变成零。

2、MOSSE滤波

提高算法的鲁棒性，作者对视频第一帧的跟踪窗口施加随机的仿射扰动，产生多组图像对滤波器进行初始化：

注意上式是元素点除，作者通过最小二乘法来求解：

求解过程我就不赘述了。经过一系列的推导，找到了Mosse滤波器的一个封闭解：

最后更新MOSSE滤波器如下：

原理解释还可以参考博客：https://blog.csdn.net/autocyz/article/details/48136473

代码解释介绍参考博客：https://blog.csdn.net/fengying2016/article/details/72598720