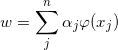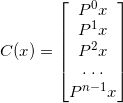ECCV2012跟踪算法CSK原理及代码解析
文章和代码下载地址：
http://www.robots.ox.ac.uk/~joao/circulant/
相信看懂相关滤波鼻祖算法MOSSE后，直接看看CSK，会产生一些疑问。本文从MOSSE出发得出CSK的相关公式，帮助大家理解。
MOSSE将相关转到频域通过最小二乘法来求解相关滤波器
：
MOSSE的解析可以参考：https://blog.csdn.net/qq_17783559/article/details/82254996
CSK提出用一个线性分类器来求解相关滤波器：
是的，换件衣服我真的就不认识了。。。。。。这个公式也叫最小二乘法，确切的名字是正则化最小二乘法（RLS），也叫做岭回归。w即为MOSSE中的相关滤波器H；
L为最小二乘法的损失函数：
y是理想的高斯响应，n表示样本数量，f(xi)表示图像xi与滤波器w的在频域内的点积，< , >表示点积同
一样，b没有实际意义，可以省略。所以
即为MOSSE中的
。
那么CSK所用的公式就只是在后面多了一个正则项
。那么加这一项有什么意义呢？？？
加正则项的目的是为了防止求得的滤波器H过拟合。通过最小二乘法求得的相关滤波器与当前帧输入的图像F的相关性是最高的，然而我们是要用求得的滤波器结果H去预测下一帧图像中目标所在的位置。因为下一帧图像不可能和当前帧的图像一模一样，所以拟合度过高反而会影响检测的准确度，所以加入正则项来减小输入图像和滤波器之间的拟合程度，使求得的滤波器H泛化能力更强。
现在基础公式是弄懂了，怎么解呢？
作者参考了支持向量机的解法，使用了核函数，接下来先介绍一下核函数，不然又处在云里雾里看不懂了
核函数
首先核函数是个啥？干啥用？
先来个定义：通过某非线性变换 φ( x) ，将输入空间映射到高维特征空间。特征空间的维数可能非常高。如果求解只用到内积运算，而在低维输入空间又存在某个函数 K(x, y) ，它恰好等于在高维空间中这个内积，即K( x, y) =<φ( x) ⋅φ( y) > 。那么求解过程中就不用计算复杂的非线性变换，而由这个函数 K(x, y) 直接得到非线性变换的内积，使大大简化了计算。这样的函数 K(x, y) 称为核函数。
举个例子：核函数K（Kernel Function）为：K(x,y')=<φ(x),φ(y)>，其中，< , >表示点积，φ(.)表示低维到高维的映射。
x=(x1,x2,x3)；y=(y1,y2,y3)
φ(x)=(x1x1,x1x2,x1x3,x2x1,x2x2,x2x3,x3x1,x3x2,x3x3)
φ(y)=(y1y1,y1y2,y1y3,y2y1,y2y2,y2y3,y3y1,y3y2,y3y3)
令x=(1,2,3)，y=(4,5,6)；
那么
φ(x)=(1,2,3,2,4,6,3,6,9)；
φ(y)=(16,20,24,20,25,30,24,30,36)；
<φ(x),φ(y)>=16+40+72+40+100+180+72+180+324=1024
因为我们把三维空间数据映射到九维空间中，所以计算复杂。
如果我们通过核函数，直接在低维空间中计算呢？
令核函数K(x,y)=(
则K(x,y)=(4+10+18)^2=1024
避开了非线性变换 φ的计算是不是方便很多，速度也快很多。所以核技巧就是用来避开这些繁琐的计算的。并且如果是将数据映射到无限维空间，通过普通的算法是无法计算的，而通过核函数却可以，如：高斯核RBF: K(x,y)=exp(-||x-y||^2)。
文归正传
1、核化的最小二乘法（KRLS）
CSK算法使用核技巧是为了提高在高维特征空间中分类样本的速度。
令φ(x)表示特征空间，K(x,x')=<φ(x),φ(x')>表示其核函数，根据支持向量机核定理可得滤波器w的解可以表示为如下的线性组合：
所以
b在实际中没有意义，不用管，可以理解直接省掉。
那么求解公式可写成如下形式：
求最小值，K是核函数，无论是高斯核函数还是什么核函数，它都可以当做已知量，所以只需要求
即可。上式除以2没有影响，等价于
通过求导来求解最小值
求得：
表示单位矩阵。
2、循环矩阵&稠密采样
循环矩阵和稠密采样都是为了求滤波器
，换言之就是为了求，理想响应
是已知的，所以求出K即可。
若
为一个
的向量，作者定义一个
的循环矩阵为：
其中可以暂时理解为输入图像，第一行表示原始的，后面的每一行都是通过循环得到的。
那么就存在如下等式：
这其实就是相关转换到频域计算的公式，作者只是把傅里叶变换边界循环补充的结构给表示出来了。之所以使用循环矩阵的形式表示出来，是为了利用循环矩阵的特性：循环矩阵的和、点积、求逆都是循环矩阵。
那么是如何通过循环矩阵来稠密采样的呢？
假设输入图片为
，为一个的向量，构造循环矩阵为：
其中，
表示循环移位操作，每次移动一个元素。
这一段是证明定理，与求解过程无关。
那么矩阵
可以定义为：
因为
所以
也是一个循环矩阵。
用循环矩阵的特性来求解：
原最小二乘法表示中：
将这里的表示成循环矩阵
表示输入图片，长度为
，所以这里的是的矩阵，且为循环矩阵。
我们把单位矩阵也看作是一个循环矩阵，即：
![\small \delta =[1,0,0,...,0]^{T},I=C(\delta )](http://img.e-com-net.com/image/info8/f0d9c4c8e5a048f990b04ff9b7f6f381.gif){kind=small}
那么
根据傅里叶变换的线性性质：
根据前面提到的这个公式：
求得：
检测的时候我们通过如下公式即可求得响应图：
作者在代码中用的高斯核，所以对应的
为：
参考博客：https://blog.csdn.net/ikerpeng/article/details/44171159