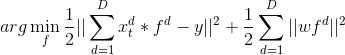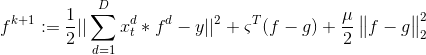相关滤波跟踪算法中ADMM的使用

相关跟踪的核心就是滤波器filters的求解，从MOSSE到KCF再到SRDCF，滤波器的模型越来越复杂，计算速度越来越慢，使得相关滤波在计算速度上的优势越来越不明显。比如较新的算法CFLB和BACF等采用了空间约束来解决边界效应，SRDCF和STRCF等使用空间正则来解决边界效应，这些解决边界效应的措施都让相关跟踪面临实时性的挑战。ADMM把一个大优化问题分成可分布式同时求解的多个子问题，通过对子问题的迭代可以快速得到滤波器的近似解。

baseline ADMM

ADMM求解以下形式的最小化问题：

该式的拉格朗日表达式为：

迭代步骤为：

example SRDCF

SRDCF原文用的是高斯-塞德尔（Gauss-Seidel）求解器，高斯-塞德尔（Gauss-Seidel）求解器也是一种迭代方法，缺点就是比ADMM要慢23333333。SRDCF最小化如下公式：

此处的为我们需要求的滤波器，也是ADMM迭代的变量之一，通过baseline的公式我们知道ADMM需要迭代两个变量，并且需要约束条件。变量不足可以构造一个辅助变量，没有约束条件我们设定约束条件，所以：

该式的拉格朗日表达式为：

迭代步骤为：

子问题的求解是不是很简单，哈哈哈哈。

子问题的求解：

转换到傅里叶域：

其中，,和都是D维的。对求导得：

子问题的求解：

没有涉及卷积不用转换到傅里叶域，直接对求导：

至此，SRDCF的ADMM迭代算法全部解完。

 

2019.04.15更新，下面给出SRDCFwithADMM的代码（注：本工程借鉴了ICCV2017目标跟踪算法BACF的相关代码）

1、代码下载地址：

https://download.csdn.net/download/qq_17783559/11117881

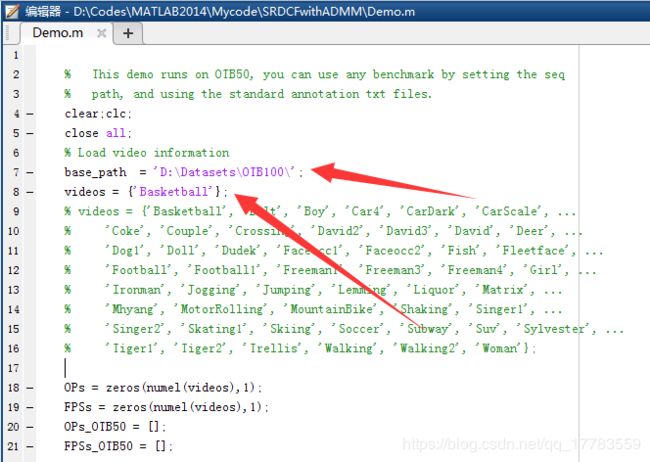
2、打开Demo更改数据集路径运行

3、运行结果：

4、run_SRDCFwithADMM.m中给出了OTB数据集的接口，可在OTB数据集中测试结果。 

 

 

2019.05.17更新，终于把一个deadline赶完了，以前的SRDCF的ADMM迭代是简化版的，便于大家理解，现在给出详细推导过程（这个推导过程是参考文章BACF来的：求别又diss我抄袭了233333，做个博客而已，搞科研对抄袭这个词真心很敏感。。。）

承接上文：

构造辅助变量，这个表示傅里叶变换，是离散傅里叶变换的2D表达式，L是图像的大小。

那么拉格朗日表达式就变为：

这里为了简化省略了D个通道的表达。

子问题g的求解：

转换到傅里叶域：

其中，,和都是D维的。对求导得：

因为分母上是D维的，使用Sherman-Morrison formula加速运算得：

这里的变量定义为。

子问题f的求解：

f没有涉及卷积不用转换到傅里叶域，直接对f求导：

至此，SRDCF的ADMM迭代算法全部解完。

 

代码简要解析：

%子问题g的求解
g_f = (((1/(T*mu)) * bsxfun(@times, yf, model_xf)) - ((1/mu) * l_f)  + h_f) - ...
            bsxfun(@rdivide,(((1/(T*mu)) * bsxfun(@times, model_xf, (S_xx .* yf))) ...
            - ((1/mu) * bsxfun(@times, model_xf, S_lx)) + (bsxfun(@times, model_xf, S_hx))), B);
        
%子问题f的求解
H_h=ifft2((mu*g_f) + l_f);
h = argmin_h(ww,mu,H_h);

其中argmin_h.m定义为：

function h = argmin_h(w1,mu, X)
     lhd= 1 ./  ((w1.^2)+ mu); % left hand
     
     h=zeros(size(X));

     % compute T for each channel
     for i = 1:size(X,3)
         h(:,:,i) = lhd.* (X(:,:,i));
     end
end

[References]

[1] 博客参考：http://www.cnblogs.com/breezedeus/p/3496819.html
[2] S. Boyd. Alternating Direction Method of Multipliers (Slides).
[3] S. Boyd et al. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers, 2010.