一、问题引入和分析
无人驾驶技术在今发展迅猛，而车道线识别检测则是无人驾驶技术的基础与保障。本篇博客将近期来博主所做的一些车道线检测的实验（无奈，有失败的，也有成功的，虽然效果一般）做一些描述，整理成笔记，一来如果能有人给出好的建议或者意见，指出我所做的是否科学合理是再好不过了，二来，也是帮助自己记忆研究历程，便于下一步研究。
为了找到一个合适的模型，或者说是方法，能够完成车道线检测的如下几个部分：
（1）直线检测
（2）曲线检测
（3）虚线、实线的检测
我们可以简单分析一下：
（1）图像预处理：首先，需要对图像进行逆透视变换，得到俯视图，同时对车道线的检测，前提条件是待检测图中尽量只有车道线信息，那么要尽可能地减少环境带来的噪声。预处理部分，后面会着重讨论到，这里只是进行场景模拟，来检验方法或者模型是否正确；
（2）直线检测：直线检测在图像识别领域算是一个入门式的课题，如今主流的方法当然是使用Hough变换对直线进行检测，对于车道线检测，也可以使用该方法进行直线部分的检测。但是，要注意两个主要的问题（后续问题，后续再具体分析）：
1>重复检测：这里的重复检测主要指非极大值抑制后仍然出现的重复检测，而是指由于曲线的存在，而导致相近位置不同角度的检测：
2>错误检测：由于曲线的引入，导致检测出角度偏差很大的直线：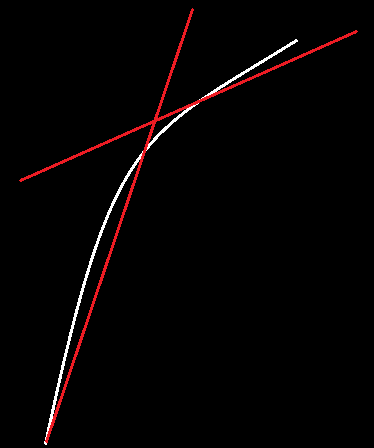
事实上，这些问题可以通过加上一些限制条件以及直线聚类的方法解决。本文暂不讨论这些问题，关于直线的筛选和聚类问题，后面文章会有详细阐述。
（3）曲线检测：该部分较为复杂，也是本文现阶段重点讨论的问题；
（4）虚线实线的检测：初步想法，可以通过直线部分，检测直线周围有效像素点所占比重来粗略估计，该部分，也不作为现阶段重点讨论的问题。
总结来说，本文现阶段，主要讨论直线检测+曲线检测的模型和方法！
二、基于改进Hough变换的曲线检测模型
（参考：http://d.wanfangdata.com.cn/Patent/CN201310717643.3/
在原方法的基础上，进行了一定的调整和改进）
2.1 基本思路
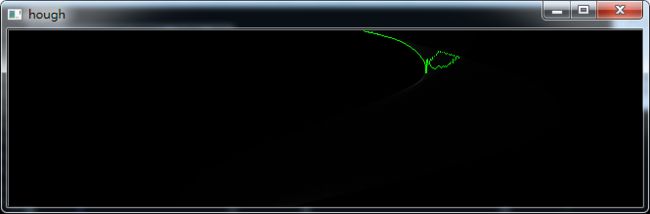
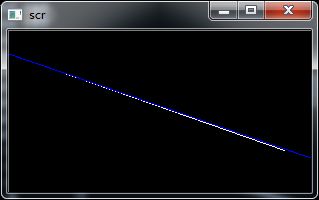
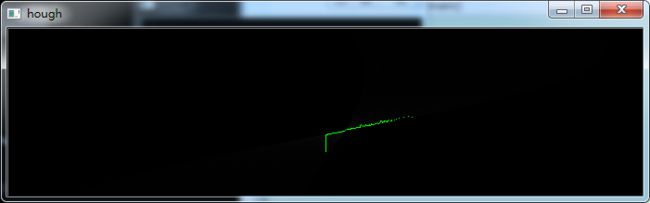
为了检测曲线，首先人为设定一个场景（这个设定可以避开环境噪声的干扰，让模型\方法的验证变得更加简单），来模拟车道线：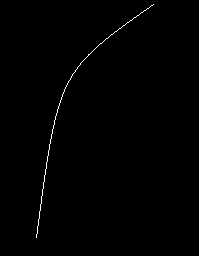
如上图所示，表示一根弯曲的车道线，现在算法的目的就是要检测这根曲线。
根据参考文献，检测上图曲线的方法描述如下：
（1）找到Hough空间中全局最大点A，作为图中曲线的主切线；
（2）在Hough空间内，以A为基点，向四周进一步搜索，若附近有大于阈值的点，则加入队列；
（3）四周均搜索不到有效点，则搜索结束，判断队列中像素点的个数，大于阈值则表示是曲线，反之，小于阈值则表示是直线；
（4）若得到结果是曲线，将队列中的像素点从Hough空间反变换到x-y坐标系下，得到最终的曲线。
2.2 具体实现
（1）对上述图像进行Hough变换，得到对应的Hough空间信息，然后遍历Hough图，得到全局最大点A，标记在图中：
（图中蓝色小点代表Hough空间中的全局最大值点）
全局最大值点代表着曲线的主切线方向；
（2）在（1）的基础上，在Hough空间中，向四周寻找大于阈值的像素点，（实际上，这里的思想是：一条直线在Hough空间中近似是一个亮点，一条曲线在Hough空间中是近似一条连续的曲线），规定向左向右搜索的方法如下：
向左搜索：搜索当前点的上、左上、左、左下、下五个点；
向右搜索：搜索当前点的上、右上、右、右下、下五个点；
向左\向右搜索退出条件：为了避免偶然性的漏检（可能恰好一段连续的曲线中间缺了一点），我们引入一个容错因子Theta
同时，考虑到曲线方向的不确定性（可能出现方向变换），如下图：
先向右后向左 先向左后向右
这种情况下，若只单纯搜索一边，很可能漏去变化方向的那一部分，如下图：
所以，为了能一次性全方位地检测出Hough空间的曲线，我们在规定如下搜索方法：
1>起始搜索点为A点
2>向右搜索，直到退出，退出点为B
3>从B点向左搜索，直到退出
4>起始搜索点回到A点
5>向左搜索，直到退出，退出点为C
6>从C点向右搜索，直到退出
结束
部分代码如下：
向左搜索：
CvPoint searchRight(int **HoughArea, IplImage* hough, CvPoint point, Lines* line)
{//找当前点的上、右上、右、右下、下
//循环搜索，直到两个方向搜索均无结果，则退出开始下一步判断
CvPoint start;//搜索的初始点
start = point;//先将point作为当前的初始点
int Max = 0;//找局部最大值
CvPoint last = start;//记录上一次最大值，本次搜索排除当前点和上一次点
int mistakes = 0;//引入一个容错因子
//****************************搜索上，右上，右，右下，下*****************************8
while(1)
{
CvPoint temp;
if(start.x >= hough->width-1 || start.y <= 0||start.y >= hough->height-1)//超出搜索范围，退出搜索
break;
//cout << "curve1" << endl;
for(int xx = 0;xx < 2; xx++)
{
for(int yy = -1;yy < 2;yy++)
{
if((xx == 0 && yy == 0)||(start.y + yy == last.y && start.x + xx == last.x))//不包括当前点
continue;
//cout << HoughArea[start.y + yy][start.x + xx] << endl;
if(HoughArea[start.y + yy][start.x + xx] > Max)
{
Max = HoughArea[start.y + yy][start.x + xx];
temp.x = start.x + xx;
temp.y = start.y + yy;
}
}
}
if(Max > Threshold)
{
//cout << Max << " ";
mistakes = 0;//容错清零
cout << "find1:"<< Max << endl;
Max = 0;
(*line).houghpoint.push_back(temp);
last = start;//保存上一次最大值
start = temp;//找到的点作为当前点继续搜索
CvScalar s;
s.val[0]=0;
s.val[1]=255;
s.val[2]=0;
//cvSet2D(hough,temp.y,temp.x,s);//set the (i,j) pixel value
}
else if(mistakes <= 5)//容错，三次
{
mistakes++;
Max = 0;
start.x = start.x + 1;
}
else//退出条件
break;//没有找到符合条件的点，退出搜索
}
//*******************************************************************************
CvPoint final;
final.x = start.x - mistakes;
final.y = start.y;
return final;
}
按照此方法得到Hough空间内的曲线检测结果：
（阈值：5）
可以看出检测效果不是很理想。由上述方法，可以看出，如果不是一个单纯连续的曲线，而有大量的噪声，则检测效果会非常差。
如此一来，为了消除“环式误检”，将检测步骤简化：
1>起始搜索点为A点
2>向右搜索，直到退出
3>起始搜索点回到A点
4>向左搜索，直到退出
结束
得到结果：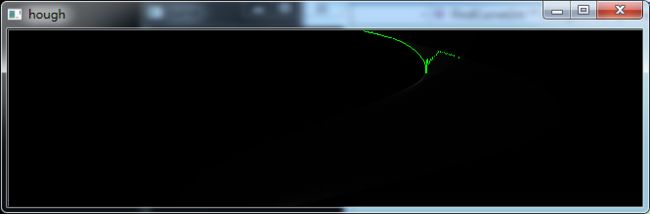
（阈值：5）
尝试其他的参数，效果不佳。实际上可以猜测得出来，右边的像素点值要比曲线下部分的大，所以检测才会跑偏。这里的结论是，噪声对Hough空间曲线检测的效果影响甚大！
（3）这里构造一个直线的结构体，含有一系列参数。
//定义一个表示曲线的结构体(包括直线)
struct Lines
{
bool curve;//是否是曲线，1表示是曲线，0表示是直线
vector point;//曲线上的点，控制点
vector houghpoint;//直线在hough空间是一个点，曲线在hough空间中应该是一条连续的曲线,x表示Dist,y表示Angle
bool dashed;//是否是虚线，1表示是虚线，0表示是实线
Lines()
{
this->curve = false;//默认是直线
this->dashed = false;//默认是实线
}
}; 其中，Houghpoint就是步骤（2）中有效点的队列。设置一个阈值，队列长度大于阈值则判断该线是曲线，否则为直线。
（4）从Hough空间反变换到X-Y坐标系下。
方法一：参考专利中的还原公式如下：
其中求出来的x，y坐标为Hough空间中（Theta，r）对应的切点。
程序中，我做出了该公式下的尝试，得到结果如下
得到结果 原图
当然，上述解算我做出了一些调整。实验发现，如果使用连续的三个点进行计算，结果是散乱无章的，所以，我间隔一定距离，取三个点进行计算。（下式MaxDist可见我博客 Hough变换（自写））
double theta1 = line.houghpoint[i].y*P/180;
double theta2 = line.houghpoint[i+5].y*P/180;
double theta3 = line.houghpoint[i+2].y*P/180;
double rho1 = line.houghpoint[i].x - MaxDist;
double rho2 = line.houghpoint[i+5].x - MaxDist;
double rho3 = line.houghpoint[i+2].x - MaxDist;
x = 0.5*cos(theta2)*rho2 + sin(theta2)*((rho1-rho2*cos(theta2-theta1))/sin(theta2-theta1))
+ 0.5*cos(theta3)*rho3 + sin(theta3)*((rho2-rho3*cos(theta3-theta2))/sin(theta3-theta2));
y = 0.5*sin(theta2)*rho2 - cos(theta2)*((rho1-rho2*cos(theta2-theta1))/sin(theta2-theta1))
+ 0.5*sin(theta3)*rho3 - cos(theta3)*((rho2-rho3*cos(theta3-theta2))/sin(theta3-theta2));
得到结果 原图
