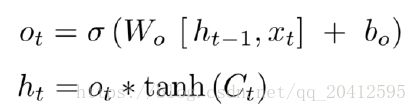Tensorflow--循环神经网络及常用函数的理解
前言：在神经网络的学习过程中，让我困惑比较多的是循环神经网络，不仅是循环神经网络比起简单的DNN、CNN理解上更难，而且它的变种也更多，模型函数有很多也很陌生，使得RNN在学习过程中更难，这里的总结更多是结合自己的疑惑来写的。
一、循环神经网络RNN简介
循环神经网络并非现今才提出来的，早在1982年就已经有了它的雏形，当时是由Saratha Sathasivam提出的霍普菲尔德网络。该网络在1986年被全连接神经网络以及一些传统的机器学习算法所取代，然而，传统的机器学习算法非常依赖于人工提取的特征，使得基于传统的机器学习的图像识别、语音识别以及自然语言处理等问题存在特征提取的瓶颈，而基于全连接的神经网络方法存在参数过多，无法利用数据中时间序列信息的问题，随着更加有效的循环神经网络结构的提出，循环神经网络挖掘数据中的时序信息以及语义信息的深度表达能力被充分利用，并在语音识别、语言模型、机器翻译以及时序问题等方面实现了突破。
二、RNN模型
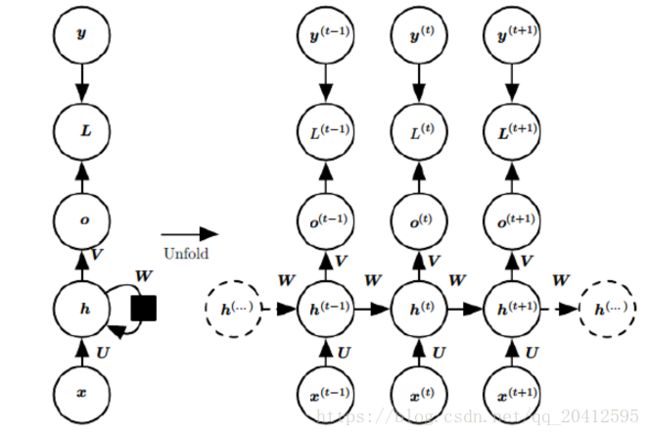
对于循环神经网络的数据输入输出，这里建议看一下Tensorflow实战Google深度学习框架（郑泽宇）这本书，这本书以数据的实际例子讲解了模型的输入和输出，可以让我们有个直观的感觉，下图为某时刻隐层单元的结构示意图。
至于具体的计算过程，这里就不展开了，列一个在网上看到的推导很详细的博客。
参数：输入到隐层的权重Ｕ、隐层到输出的权重Ｖ，自身递归的权重Ｗ
循环层输出：
,其中f是激活函数
输出层输出：
,其中g是激活函数。
图展示了RNN的前向传播的计算过程
RNN反向传播算法的思路和DNN是一样的，即通过梯度下降法一轮轮的迭代，得到合适的RNN模型参数U,W,V,b,c。由于我们是基于时间反向传播，所以RNN的反向传播有时也叫做BPTT(back-propagation through time)。当然这里的BPTT和DNN也有很大的不同点，即这里所有的U,W,V,b,c在序列的各个位置是共享的，反向传播时我们更新的是相同的参数。
为了简化描述，这里的损失函数我们为对数损失函数，输出的激活函数为softmax函数，隐藏层的激活函数为tanh函数。
对于RNN，由于我们在序列的每个位置都有损失函数，因此最终的损失L为：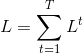
个人感觉普通的循环神经网络还是比较简单的，这里不做过多的展开了，需要特别指出的是，理论上循环神经网络可以支持任意长度的序列，然而在实际的训练过程中，如果序列过长，一方面会导致优化时出现梯度消失和梯爆炸的问题，另一方面，展开后的前馈神经网络会占用过大的内存，所以实际中一般会规定一个最大的长度，当序列长度超过规定长度之后会对序列进行截断。
三、长短时记忆网络（LSTM）
前面提到的RNN解决了对之前的信息保存的问题。但是存在长期依赖的问题。看电影的时候，某些情节的推断需要依赖很久以前的一些细节。很多其他的任务也一样。很可惜随着时间间隔不断增大时，RNN 会丧失学习到连接如此远的信息的能力也就是说，记忆容量有限，一本书从头到尾一字不漏的去记，肯定离得越远的东西忘得越多。
LSTM是RNN一种，大体结构几乎一样。区别是？
- 它的“记忆细胞”改造过。
- 该记的信息会一直传递，不该记的会被“门”截断。
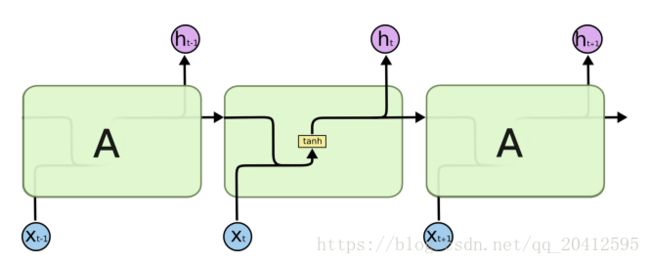
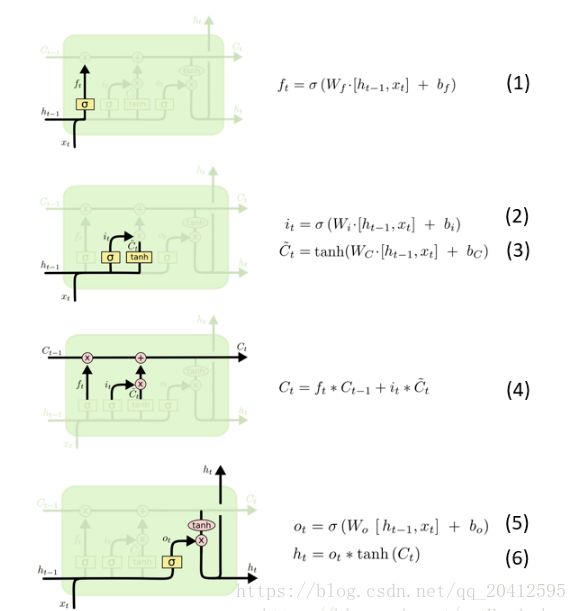
网上介绍LSTM比较流行的都是借用的这张图，确实很清楚，这张图表示的。
从上图中可以看出，在每个序列索引位置t时刻向前传播的除了和RNN一样的隐藏状态h(t)，还多了另一个隐藏状态，如图中上面的长横线。这个隐藏状态我们一般称为细胞状态(Cell State)，记为C(t)。如下图所示：
LSTM在在每个序列索引位置t的门一般包括遗忘门，输入门和输出门三种。下面我们就来研究上图中LSTM的遗忘门，输入门和输出门以及细胞状态。
LSTM之遗忘门
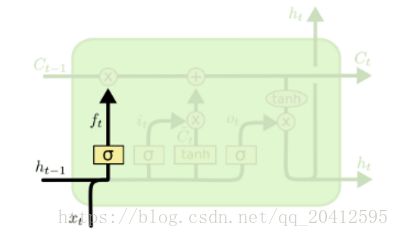
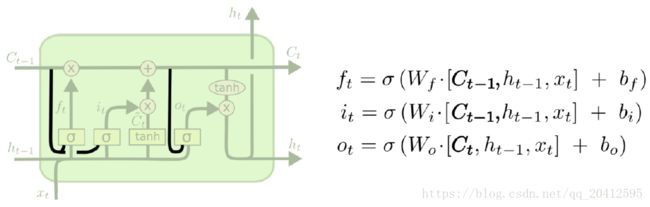
遗忘门（forget gate）顾名思义，是控制是否遗忘的，在LSTM中即以一定的概率控制是否遗忘上一层的隐藏细胞状态。遗忘门子结构如下图所示：
图中输入的有上一序列的隐藏状态h(t−1)和本序列数据x(t)，通过一个激活函数，一般是sigmoid，得到遗忘门的输出f(t)。由于sigmoid的输出f(t)在[0,1]之间，因此这里的输出
代表了遗忘上一层隐藏细胞状态的概率。
用数学表达式即为： ![f_{t}=\sigma (W_{f}h_{t-1}+U_{f}x_{t}+b_{f}) = sigmoid(W_{f}[h_{t-1},x_{t}]+b_{f})](http://img.e-com-net.com/image/info8/a9b75afb4aef466bab260d68ebcf8f46.gif){kind=small}
通过“门”让信息选择性通过，来去除或者增加信息到细胞状态，注意理解的时候千万别把C(t)理解成了一个数，它其实是一个向量，在表示一种状态，当然啦，f(t)也是一个向量，千万别理解成了一个数，否则对神经网络的理解就会有很大的问题。
- 包含一个sigmoid神经网络层 和一个pointwise乘法操作（这里的点乘就是对应元素相乘）
- Sigmoid 层输出0到1之间的概率值，描述每个部分有多少量可以通过,。
- 0代表“不许任何量通过”，1就指“允许任意量通过”
第1步：决定从“细胞状态”中丢弃什么信息 => “忘记门”
LSTM之输入门
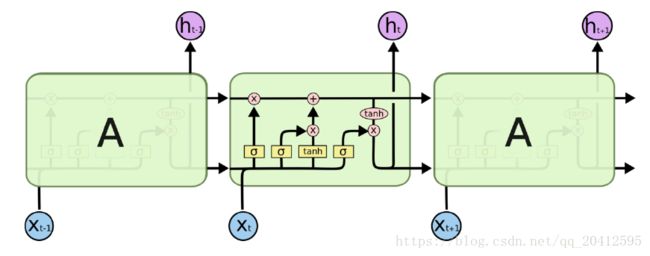
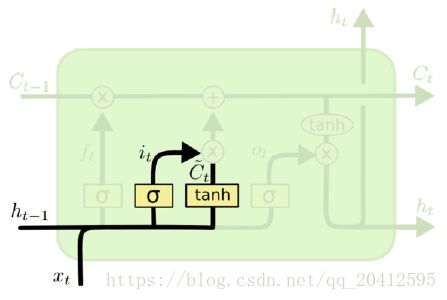
输入门（input gate）负责处理当前序列位置的输入，它的子结构如下图：
从图中可以看到输入门由两部分组成，第一部分使用了sigmoid激活函数，输出为
,第二部分使用了tanh激活函数，输出为
, 两者的结果后面会相乘再去更新细胞状态。用数学表达式即为：
![i_{t}=\sigma (W_{i}h_{t-1}+U_{i}x_{t}+b_{i}) = sigmoid(W_{i}[h_{t-1},x_{t}]+b_{i})](http://img.e-com-net.com/image/info8/09bc9b4ec144421487e1ca40e70d5e0a.gif){kind=small}
![\widetilde{C_{t}}=tanh (W_{C}h_{t-1}+U_{C}x_{t}+b_{C}) = tanh(W_{C}[h_{t-1},x_{t}]+b_{C})](http://img.e-com-net.com/image/info8/9d78e0ae109a41b0834075f3fabf849b.gif){kind=small}
注意到输出是0到1之间的概率值，描述每个部分有多少量可以通过，但是输出是[-1,1]，两者相乘即是这次新信息要以多大的程度来进行更新。注意再次的强调，这里的是一个向量，同理也是一个向量，两个向量点乘之后还是一个向量。
第2步：决定放什么新信息到“细胞状态”中
LSTM之细胞状态更新
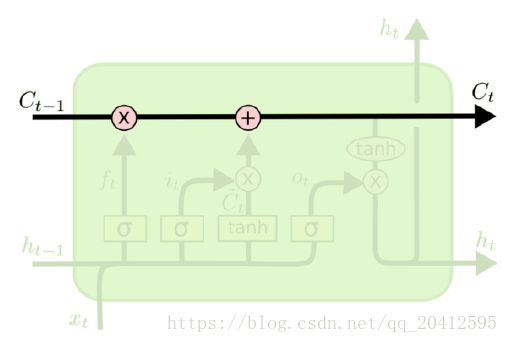
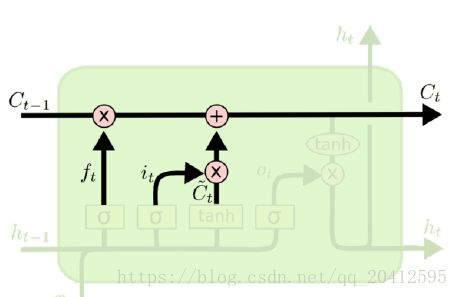
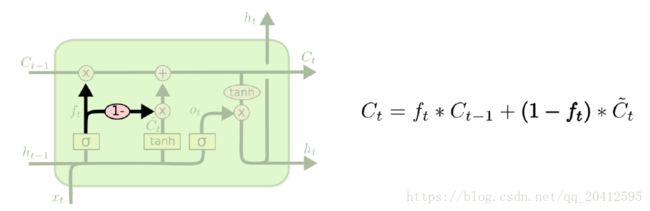
在研究LSTM输出门之前，我们要先看看LSTM之细胞状态。前面的遗忘门和输入门的结果都会作用于细胞状态C(t)。我们来看看从细胞状态C(t−1)如何得到C(t)。如下图所示：
细胞状态C(t)由两部分组成，第一部分是C(t−1)和遗忘门输出f(t)的乘积，第二部分是输入门的和的乘积，即：
，这里的
是对应元素相乘。
- 更新C(t−1)为C(t)
- 把旧状态与ft相乘，丢弃掉我们确定需要丢弃的信息
- 加上
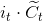。这就是新的候选值，根据我们决定更新每个状态的程度进行变化。
第3步：更新“细胞状态”
LSTM之输出门
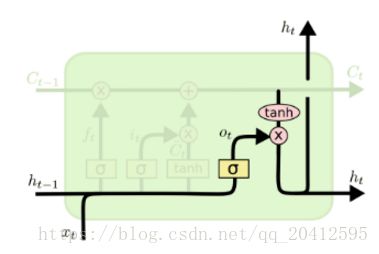
有了新的隐藏细胞状态C(t)，我们就可以来看输出门了，子结构如下：
从图中可以看出，隐藏状态h(t)的更新由两部分组成，第一部分是o(t), 它由上一序列的隐藏状态h(t−1)和本序列数据x(t)，以及激活函数sigmoid得到，第二部分由隐藏状态C(t)和tanh激活函数组成, 即：
LSTM的变体
变种1
- 增加“peephole connection”
- 让 门层 也会接受细胞状态的输入。
变种2
- 通过使用 coupled 忘记和输入门
- 之前是分开确定需要忘记和添加的信息，这里是一同做出决定。
当然，LSTM的变种还有很多，这里就不列出了。
四、LSTM细节的问题
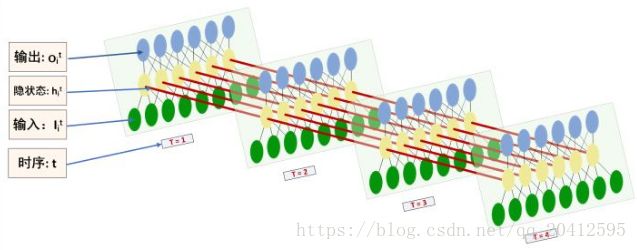
Recurrent NN是在time_step上的拓展的这一特性。MLP好理解，CNN也好理解，但Recurrent NNs，不是很容易从图中直接看出拓扑结构。这里借鉴了知乎大神的一些观点
RecurrentNNs的拓扑结构图：
BasicLSTMCell中num_units参数解释
这里的观点参考于BasicLSTMCell中num_units参数解释，觉得讲的挺清楚的。
BasicLSTMCell 是最简单的LSTMCell，源码位于：/tensorflow/contrib/rnn/python/ops/core_rnn_cell_impl.py。
BasicLSTMCell 继承了RNNCell，源码位于：/tensorflow/python/ops/rnn_cell_impl.py
注意事项：
1.input_size这个参数不能使用，使用的是num_units
2.state_is_tuple 官方建议设置为True。此时，输入和输出的states为c(cell状态)和h（输出）的二元组
指定num_units cell = tf.contrib.rnn.BasicLSTMCell(num_units, forget_bias=1.0, state_is_tuple=True) 指定batch_size,将c和h全部初始化为0，shape全是batch_size * num_units _initial_state = cell.zero_state(batch_size, tf.float32)
class BasicLSTMCell(RNNCell):
"""Basic LSTM recurrent network cell.
The implementation is based on: http://arxiv.org/abs/1409.2329.
We add forget_bias (default: 1) to the biases of the forget gate in order to
reduce the scale of forgetting in the beginning of the training.
It does not allow cell clipping, a projection layer, and does not
use peep-hole connections: it is the basic baseline.
For advanced models, please use the full LSTMCell that follows.
"""
def __init__(self, num_units, forget_bias=1.0, input_size=None,
state_is_tuple=True, activation=tanh):
"""Initialize the basic LSTM cell.
Args:
num_units: int, The number of units in the LSTM cell.
forget_bias: float, The bias added to forget gates (see above).
input_size: Deprecated and unused.
state_is_tuple: If True, accepted and returned states are 2-tuples of
the `c_state` and `m_state`. If False, they are concatenated
along the column axis. The latter behavior will soon be deprecated.
activation: Activation function of the inner states.
"""
if not state_is_tuple:
logging.warn("%s: Using a concatenated state is slower and will soon be "
"deprecated. Use state_is_tuple=True.", self)
if input_size is not None:
logging.warn("%s: The input_size parameter is deprecated.", self)
self._num_units = num_units
self._forget_bias = forget_bias
self._state_is_tuple = state_is_tuple
self._activation = activation
@property
def state_size(self):
return (LSTMStateTuple(self._num_units, self._num_units)
if self._state_is_tuple else 2 * self._num_units)
@property
def output_size(self):
return self._num_units
def __call__(self, inputs, state, scope=None):
"""Long short-term memory cell (LSTM)."""
with vs.variable_scope(scope or "basic_lstm_cell"):
# Parameters of gates are concatenated into one multiply for efficiency.
if self._state_is_tuple:
c, h = state
else:
c, h = array_ops.split(value=state, num_or_size_splits=2, axis=1)
# 线性计算 concat = [inputs, h]W + b
# 线性计算，分配W和b，W的shape为（2*num_units, 4*num_units）,
#b的shape为（4*num_units,）,共包含有四套参数，
# concat shape(batch_size, 4*num_units)
# 注意：只有cell 的input和output的size相等时才可以这样计算，否则要定义两套W,b.
#每套再包含四套参数
concat = _linear([inputs, h], 4 * self._num_units, True, scope=scope)
# i = input_gate, j = new_input, f = forget_gate, o = output_gate
i, j, f, o = array_ops.split(value=concat, num_or_size_splits=4, axis=1)
new_c = (c * sigmoid(f + self._forget_bias) + sigmoid(i) *
self._activation(j))
new_h = self._activation(new_c) * sigmoid(o)
if self._state_is_tuple:
new_state = LSTMStateTuple(new_c, new_h)
else:
new_state = array_ops.concat([new_c, new_h], 1)
return new_h, new_state这里直接给出结论，num_units这个参数的大小就是LSTM输出结果的维度。例如num_units=128， 那么LSTM网络最后输出就是一个128维的向量。
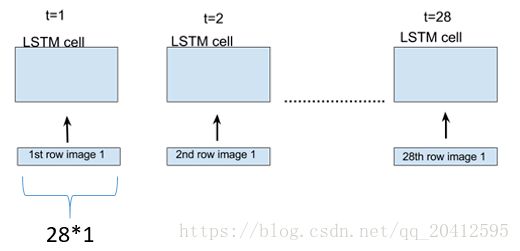
假设在我们的训练数据中，每一个样本 x 是 28*28 维的一个矩阵，那么将这个样本的每一行当成一个输入，通过28个时间步骤展开LSTM，在每一个LSTM单元，我们输入一行维度为28的向量，如下图所示。
对每一个LSTM单元，参数 num_units=128 的话，就是每一个单元的输出为 128*1 的向量，在展开的网络维度来看，如下图所示，对于每一个输入28维的向量，LSTM单元都把它映射到128维的维度， 在下一个LSTM单元时，LSTM会接收上一个128维的输出，和新的28维的输入，处理之后再映射成一个新的128维的向量输出，就这么一直处理下去，直到网络中最后一个LSTM单元，输出一个128维的向量。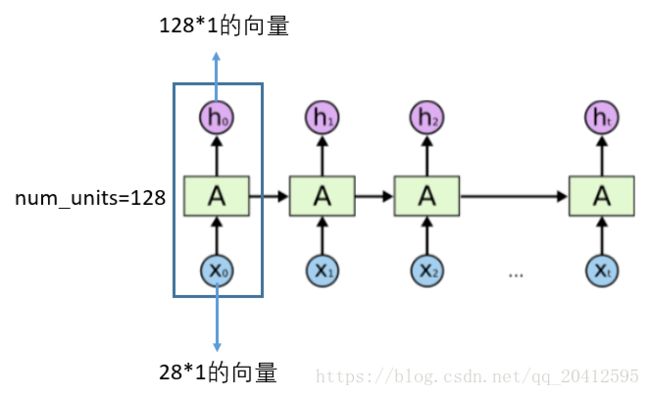
从LSTM的结构和公式入手看
看
参数 num_units=128 的话，
- 对于公式 (1) ，h=128*1 维， x=28*1 维，[h,x]便等于156*1 维，W=128*156 维，所以 W*[h,x]=128*156 * 156*1=128*1, b=128*1 维, 所以 f=128*1+128*1=128*1 维；
- 对于公式 (2) 和 (3)，同上可分析得 i=128*1 维，C(~)=128*1 维;
- 对于公式 (4) ，f(t)=128*1, C(t-1)=128*1, f(t) .* C(t-1) = 128*1 .* 128*1 = 128*1 , 同理可得 C(t)=128*1 维;
- 对于公式 (5) 和 (6) ， 同理可得 O=128*1 维， h=O.*tanh(C)=128*1 维。
所以最后LSTM单元输出的h就是 128*1 的向量。其实从源码中我们也可以看到。
另外几个需要注意的地方：
- cell 的状态是一个向量，是有多个值的。
- 上一次的状态 h(t-1)是怎么和下一次的输入 x(t) 结合（concat）起来的，直白的说就是把二者直接拼起来，比如 x是28位的向量，h(t-1)是128位的，那么拼起来就是156位的向量，就是这么简单。
- cell 的权重是共享的，这是什么意思呢？它只是代表了一个 cell 在不同时序时候的状态，所有的数据只会通过一个 cell，然后不断更新它的权重。
- 那么一层的 LSTM 的参数有多少个？我们知道参数的数量是由 cell 的数量决定的，这里只有一个 cell，所以参数的数量就是这个 cell 里面用到的参数个数。假设 num_units 是128，输入是28位的，那么根据上面，可以得到，四个小黄框的参数一共有 （128+28）*（128）*（4），也就是156 * 512，可以看看 TensorFlow 的最简单的 LSTM 的案例，中间层的参数就是这样，不过还要加上输出的时候的激活函数的参数，假设是10个类的话，就是128*10的 W 参数和10个bias 参数
- cell 最上面的一条线的状态即 s(t) 代表了长时记忆，而下面的 h(t)则代表了工作记忆或短时记忆
tf.nn.rnn_cell.BasicLSTMCell函数用法
以下内容是借鉴这篇博客的
tf.nn.rnn_cell.BasicLSTMCell(n_hidden, forget_bias=1.0, state_is_tuple=True): n_hidden表示神经元的个数，forget_bias就是LSTM们的忘记系数，如果等于1，就是不会忘记任何信息。如果等于0，就都忘记。state_is_tuple默认就是True，官方建议用True，就是表示返回的状态用一个元组表示。这个里面存在一个状态初始化函数，就是zero_state（batch_size，dtype）两个参数。batch_size就是输入样本批次的数目，dtype就是数据类型
import tensorflow as tf
batch_size = 4
input = tf.random_normal(shape=[3, batch_size, 6], dtype=tf.float32)
cell = tf.nn.rnn_cell.BasicLSTMCell(10, forget_bias=1.0, state_is_tuple=True)
init_state = cell.zero_state(batch_size, dtype=tf.float32)
output, final_state = tf.nn.dynamic_rnn(cell, input, initial_state=init_state, time_major=True)
time_major如果是True，就表示RNN的steps用第一个维度表示，建议用这个，运行速度快一点。
如果是False，那么输入的第二个维度就是steps。
如果是True，output的维度是[steps, batch_size, depth]，反之就是
[batch_size, max_time, depth]。就是和输入是一样的
final_state就是整个LSTM输出的最终的状态，包含c和h。
c和h的维度都是[batch_size， n_hidden]
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
print(sess.run(output))
print(sess.run(final_state))
注意这里要明确的是c和h的维度与W的维度无关，这里的维度先确定，然后W的维度
自然而然就确定下来了
输出：
[[[-0.17837059 0.01385643 0.11524696 -0.04611184 0.05751593 -0.02275656
0.10593235 -0.07636188 0.12855089 0.00768109]
[ 0.07553699 -0.23295973 -0.00144508 0.09547552 -0.05839045 -0.06769165
-0.41666976 0.3499622 -0.01430317 -0.02479473]
[ 0.08574327 -0.05990489 0.06817424 0.03434218 0.10152793 -0.10594042
-0.25310516 0.07232092 0.064815 0.0659876 ]
[ 0.15607212 -0.31474397 -0.06477047 -0.06982201 -0.05489461 0.0188695
-0.30281037 0.39494631 -0.05267519 -0.03253869]]
[[-0.03209484 -0.06323308 -0.25410452 -0.10886975 0.00253956 -0.08053195
0.18729064 -0.0788438 0.14781287 -0.20489833]
[ 0.3164973 -0.10971865 -0.35004857 -0.00576114 -0.08092841 0.00883496
-0.17579219 0.19092172 -0.0237403 -0.43207553]
[ 0.2409949 -0.17808972 -0.1486263 0.02179234 -0.21656732 0.0522153
-0.21345614 0.18841118 -0.0094095 -0.34072629]
[ 0.12034108 -0.23767222 0.03664704 0.13274716 -0.04165298 -0.04095407
-0.31182185 0.36334303 -0.01146755 0.05028744]]
[[-0.12453001 -0.1567502 -0.16580626 -0.03544752 0.06869993 0.09097657
-0.02214662 -0.18668351 0.06159507 -0.35843855]
[ 0.2010586 0.03222289 -0.31237942 0.01898964 -0.08158109 -0.02510365
0.02967031 0.12587228 -0.22250202 -0.08734316]
[ 0.14316584 0.02029586 -0.1062321 0.02968353 -0.02318866 0.07653226
-0.13600637 -0.00440343 0.07305693 -0.26385978]
[ 0.23669831 -0.13415271 -0.10488234 0.03128149 -0.11343875 -0.05327768
-0.22888957 0.17797095 -0.02945257 -0.18901967]]]
LSTMStateTuple(c=array(
[[-0.72714508, 0.32974839, 0.67756736, 0.11421457, 0.39167076,
0.31247479, 0.0755761 , -0.62171376, 0.58582318, -0.19749212],
[ 0.44815305, 0.06901363, -0.88840145, 0.22841501, 0.04539755,
0.17472507, -0.50547051, 0.46637267, -0.07522876, -0.80750966],
[-0.19392423, -0.16717091, -0.19510591, -0.48713976, -0.18430954,
0.1046299 , 0.30127296, -0.03556332, -0.37671563, -0.1388765 ],
[-0.47982571, 0.2172934 , 0.56419176, 0.15874679, 0.29927608,
0.16362543, 0.11525643, -0.47210076, 0.56833684, -0.18866351]], dtype=float32),
h=array(
[[-0.36339632, 0.17585619, 0.29174498, 0.03471305, 0.2237694 ,
0.13323013, 0.03002708, -0.26190156, 0.28289214, -0.12495621],
[ 0.1543802 , 0.04264591, -0.27087522, 0.084597 , 0.01555507,
0.10631134, -0.23696639, 0.2758382 , -0.03724022, -0.4389703 ],
[-0.14088678, -0.10961234, -0.10831701, -0.19923639, -0.10324109,
0.04290821, 0.10720341, -0.01477169, -0.14518294, -0.04280116],
[-0.34502122, 0.10841226, 0.32169446, 0.03053316, 0.20867576,
0.04689977, 0.03286072, -0.11068864, 0.37977526, -0.12110116]], dtype=float32))
作者：UESTC_C2_403
原文：https://blog.csdn.net/UESTC_C2_403/article/details/73353145?utm_source=copy
参考资料：
https://blog.csdn.net/notHeadache/article/details/81164264
https://blog.csdn.net/UESTC_C2_403/article/details/73353145