图像正交变换

正交变换时数字图像处理的一种有效工具。图像不仅可以在空间域表示，也可以对其进行正交变换到频域进行分析处理。在图像增强、图像复原、图像特征处理、图像编码中都经常采用图像变换技术。

离散傅里叶变换

一维离散傅里叶变换

对于有限长的数字序列 f(x),x=0,1,...,N−1 ，一维DFT定义为：
F(u)=∑N−1x=0f(x)e−j2πuxN

一维傅里叶反变换IDFT定义为：
f(x)=1N∑N−1x=0F(u)ej2πuxN

f(x)和F(u)为离散傅里叶变换对，表示为： f(x)⇆F(u)
设 W=e−j2πN ,则一维的DFT和IDFT表示为：
F(u)=∑N−1x=0f(x)Wux
f(x)=1N∑N−1x=0F(u)W−ux

一维快速傅里叶变换

FFT原理

Wu±rN=Wu
Wu±N2=−Wu

---

---

FFT算法推导
W因子如下特性:
Wk2N=Wk2N
DFT可以表示为：
F(u)=∑N/2−1x=0f(2x)W2uxN+∑N/2−1x=0f(2x+1)Wu(2x+1)N=∑N/2−1x=0f(2x)WuxN/2+∑N/2−1x=0f(2x+1)WuxN/2WuN

令M= N2 ，

F(u)=Fe(u)+WuNF0(u)

F(u+M)=Fe(u)−WuNF0(u)

将原函数分为奇数项和偶数项，通过不断的一个奇数一个偶数的相加减，得到最终结果。

---

---

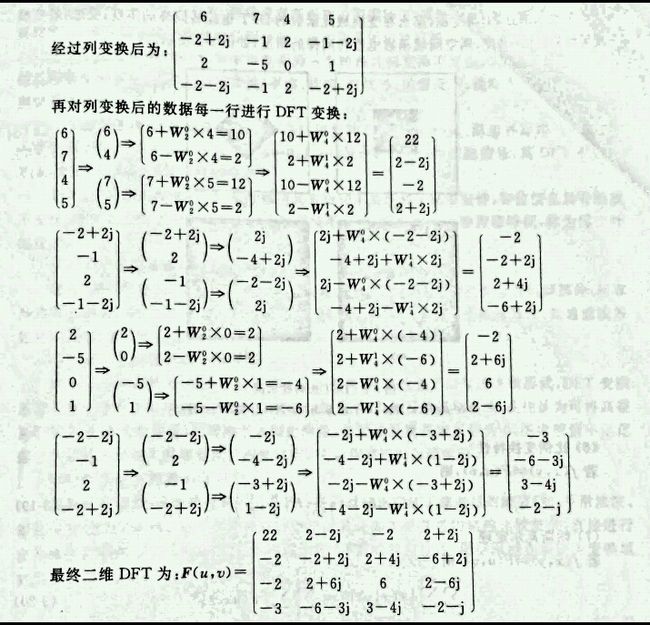
二维离散傅里叶变换

代码：

I=imread('106.jpg');
subplot(1,3,1),imshow(I),title('106 原图');
grayI=rgb2gray(I);   
%彩色图像灰度化
DFTI=fftshift(fft2(grayI));
%计算傅里叶变换并移位
ADFTI=abs(DFTI);
%求模
subplot(1,3,2),imshow(log(1+ADFTI),[]),title('106 频谱图1');
top=max(ADFTI(:));
%求模的最大值
bottom=min(ADFTI(:));
%求模的最小值
ADFTI=(ADFTI-bottom)/(top-bottom)*100;
%将模规格化到[0 100]
subplot(1,3,3),imshow(ADFTI),title('106 频谱图2');

DFTI中的数据是经过搬移的傅里叶变换系数，为复数，不能直接通过MATLAB函数显示，调用abs函数对其求模ADFTI，频谱图1是对ADFTI进行对数运算以观察图像DFT结果，频谱图2是将ADFT1归一化扩大100倍显示，对比明显

---

---

二维离散傅里叶变换的性质

1）可分性
F(u,v)=∑M−1x=0∑N−1y=0f(x,y)⋅e−j2πxuM⋅e−j2πyuN=Fx{Fy[f(x,y)]}

2）线性
F[a1f1(x,y)+a2f2(x,y)]=a1F[f1(x,y)]+a2F[f2(x,y)]

---

---

3）共轭对称性
若 f(x,y)⇆F(u,v)，F∗(−u,−v)是f(−x,−y)的DFT共轭函数，则
F(u,v)=F∗(−u,−v)

---

---

4）平移性
时域位移对应频域相移

---

---

5）旋转性
若把 f(x,y)与F(u,v) 都表示为极坐标形式，若 f(γ,θ)⇆F(k,ϕ) ，则
f(γ,θ+θ0)⇆F(k,ϕ+θ0)
空间域旋转，频域也旋转同样角度

---

---

6）比例的变换特性
f(ax,bx)⇆1|ab|F(ua,vb)

---

---

7）帕斯瓦尔定理

∑M−1x=0∑N−1y=0|f(x,y)|2=∑M−1u=0∑N−1v=0|F(u,v)|2

帕斯瓦尔定理也称为能量保持定理，变换前后不损失能量，只是改变表现形式，是变换编码的基本条件

---

---

8）卷积定理

f(x,y)∗g(x,y)⇆F(u,v)⋅G(u,v)
f(x,y)⋅g(x,y)⇆F(u,v)∗G(u,v)

---

---

傅里叶变换在图像处理中的应用

1）傅里叶描绘子
从原始图像产生的数值、符号或者图形成为图像特征。表征图像特征的一系列符号称为描绘子。
描绘子具有多种特性：几何变换不变性等
一个闭合区域，区域上的边界点(x,y)，用复数表示(x+iy).沿边界跟踪一周，得到一个复数序列， z(n)=x(n)+iy(n) ，z(n)为周期信号，其DFT系数用Z(k)表示—称为傅里叶描绘子（平移旋转不变性等）

---

2）图像滤波中应用
设计滤波器：高通低通带通（阻）等等

---

3）图像压缩中应用
高频一般为噪声信号，合理设置高频信号为0，图像质量不会改变多少

---

4）卷积特性

fg=g∗f
Fg(u,v)=G(u,v)⋅F(u,v)
fg=IDFT(Fg)
，先分别逆变换后点乘再逆变换得到f，降低卷积计算量

---

---

---

离散余弦变换

离散余弦变换（DCT）是一种与傅里叶变换紧密相连的数学运算。

一维离散余弦变换

DCT:
F(u)=C(u)2N−−√∑N−1x=0f(x)cos(2x+1)uπ2N
u=0,...,N−1

IDCT:
f(x)=2N−−√∑N−1x=0C(u)F(u)cos(2x+1)uπ2N
x=0,...,N−1

C(u)={ 12√1u=0u=1,...,N−1 

二维离散余弦变换

推广：
DCT:
F(u,v)=2MN−−−−√C(u)C(v)∑M−1x=0∑N−1y=0f(x,y)cos(2x+1)uπ2Ncos(2y+1)vπ2M
x,u=0,...,M−1

IDCT:
f(x,y)=2MN−−−−√∑M−1u=0∑N−1v=0C(u)C(v)F(u,v)cos(2x+1)uπ2Ncos(2y+1)vπ2M
y,v=0,...,N−1

C(u),C(v)={ 12√1u,v=0u,v=1,...,N−1 

---

代码：

I=imread('099.jpg');
figure;
imshow(I),title(' 原图');
grayI=rgb2gray(I);
DCTI=dct2(grayI);
%离散余弦变换
ADCTI=abs(DCTI);
top=max(ADCTI(:));
bottom=min(ADCTI(:));
ADCTI=(ADCTI-bottom)/(top-bottom)*100;
%将模规格化到[0 100]
figure;
imshow(ADCTI),title('DCT频谱图');

可以看出能量主要集中在左上角低频分量处

---

---

离散余弦变换在图像处理中的应用

离散余弦变换主要用于对图像（静止或运动）进行有损数据压缩。（静止图像编码标准JPEG、运动图像编码标准MPEG中都用到了）——由于该变换具有很强的能量集中特性：大多数的能量都集中在离散余弦变换后的低频部分，压缩编码效果较好。

具体做法：先把图像分成 8×8 块，对每个方块进行二维DCT变换，变换后的能量主要集中在低频区。对DCT系数量化，给高频系数大间隔量化，低频部分小间隔量化，舍弃绝大部分数据为取值很小或为0的高频数据，降低数据量，同时保证重构图像不发生显著失真。

---

---

K-L变换

K-L变换时建立在统计特性基础上的一种变换，又称为霍特林变换或主成分分析。K-L变换的突出优点是相关性好，是**均方误差**MSE意义下的最佳变换，在数据压缩有重要地位。

K-L变换原理

1）K-L展开式
设有一个连续的随机函数 x(t),T1⩽t⩽T2,可用已知正交函数集{ϕj(x),j=1,2...}展开：
x(t)=a1ϕ1(t)+....+ajϕj(t)
其中 aj为展开系数，ϕj(t)为连续正交函数，满足下式：
∏T2T1ϕn(t)⋅ϕ∗m(t)dt={ 10m=nm≠n 

ϕn(t)与ϕ∗m(t) 为共轭复数式

X=∑nj=1ajϕj=ΦA

Φ=(ϕ1ϕ2...ϕn)=⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪ ϕ1(1)ϕ1(2)...ϕ1(n)ϕ2(1).........ϕn(1)

---

---

2）离散K-L变换
用有限项估计X，即：
X^=∑mj=1ajϕj=ΦA
由此引起的均方误差：
ϵ2¯=E[(X−X¯)T(X−X¯)]=E[∑∞j=m+1ajuj⋅∑∞j=m+1ajuj]
因u为正交归一向量系
令 Ψ=E[XXT] ,则：
ϵ2¯=∑∞j=m+1uTjΨuj
利用拉格朗日乘数法求均方误差取极值时的u，拉格朗日函数为：
h(uj)=∑∞j=m+1uTjΨuj−∑∞j=m+1λ[uTjuj−1]
对 uj 求导，得：
(Ψ−λjI)uj=0,j=m+1,...,∞
其中 λj是X的自相关矩阵Ψ的特征值，uj是对应的特征向量

以X的自相关矩阵 Ψ 的m个最大特征值对应的特征向量来逼近X时，其截断均方误差具有极小性质：
ϵ2¯=∑∞j=m+1λj
这m个特征向量所组成的正交坐标系U称作X所在的n维空间的m维K-L变换坐标系。
满足：
A=UTX
X=UA
其中， U=(u1,...,um)

3）K-L变换的性质

通过K-L变换，消除了原有向量X的各分量之间的相关性，即变换后数据A的各分量之间的信息是相互独立的。
采用大特征值对应的特征向量组成变换矩阵，能对应地保留原向量中方差最大的成分，K-L变换起到了减小相关性、突出差异性的效果，称之为主成分分析|PCA—是将多个变量通过线性变换以选出较少个数重要变量的多元统计方法，又称主分量分析。

4）K-L坐标系的产生矩阵

前面的分析中，数据X的K-L坐标系的产生矩阵采用的是自相关矩阵 Ψ=E[XXT] ,由于总体均值向量 μ 常常没有什么意义，常把数据的协方差矩阵作为K-L坐标系的产生矩阵。
∑=E[(X−μ)(X−μ)T]

---

---

图像K-L变换

将二维图像采用行堆叠或列堆叠转换为一维处理。设M × N图像f(x,y),在某个传输通道传输了L次，由于受到各种因素的随机干扰，接收的图像是一个图像集合：
{f1(x,y),....,fL(x,y)}
采用行堆叠表示为MN维向量：
fi=⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪ fi(0,0)fi(0,1)...fi(M−1,N−1)

定义f向量的协方差矩阵和相应变换核矩阵：
∑f=E[(f−μf)(f−μf)T]≈1L[∑Li=1fifTi]−ufuTf
显然， ∑f是MN×MN维的矩阵
设 λ1和ui为∑f 的特征值和特征向量，且降序排列：
λ1>λ2>...>λM×N
K-L变换矩阵U:
U=(u_1,u_2,...,u_{M\times N})=\left\{\begin{array}{rcl}\ u_{11}&u_{21} &...&u_{MN1}\\ u_{12} &... \\...\\u_{1MN}&... \end{array}\right. U=(u1,u2,...,uM×N)=⎧⎩⎨⎪⎪⎪⎪⎪⎪ u11u12...u1MNu21.........uMN1

二维K-L变换表示为：
F=UT(f−uf)
f−uf 为原始图像f减去平均值向量 uf ,称为中心化图像向量。离散K-L变换向量F是中心化向量 f−uf 与变换核矩阵U相乘所得的结果。

---

---

小波变换

小波变换被应用到数字图像处理的多个方面，如图像平滑，边缘检测，图像分割及压缩编码等。

---

---

概述

波被定义为时间或空间的一个振荡函数。小波具有在时间上集中能量的能力，是分析瞬变的，非平稳的或时变现象的一个工具。

如正弦曲线在整个横坐标t上等振幅振荡，具有无限能量，而小波具有蔚然一个集结的有限能量。

---

---

傅里叶系数的正交基是由频率为w的sin wt和cos wt组成，傅里叶变换其实就是求傅里叶级数的系数。
小波展开就是由具有两个参数的小波构成基展开函数，即：
f(t)=∑a∑bαa,bψa,b(t)
所谓小波变换即是计算系数集 αa,b 。与傅里叶变换不同的是，小波展开集不是唯一的。

小波

1）定义：
∫Rψ(t)dt=0

对其进行平移和伸缩产生函数族 ψa,b(t)=1a√ψ(t−ba)a,b∈R,a≠0

ψ(t)称为基小波或母小波，a称为伸缩因子（尺度因子），b为平移因子，ψa,b(t)称为ψ(t)生成的连续小波

定义：若满足：
Cψ=∫R|Ψ(w)|2|w|dw<∞
则称 ψ(t) 为允许小波，上式称为允许性条件。其中 Ψ(w)=∫Rψ(t)e−jwtdt
因 Ψ(w)|w=0=∫Rψ(t)dt=0,允许小波一定是基小波。

一维小波：
1）Haar小波
2）Morlet小波
3）墨西哥草帽（Mexico Hat）小波

连续小波变换：
冗余与再生核

离散小波变换：
小波框架与Reisz基
二进小波

正交小波与多分辨分析

函数正交小波分解：
Mallat算法

紧支集正交小波基的构造:
Daubechies小波的构造

二唯小波变换：