视觉slam14讲——第11讲后端2

本系列文章是记录学习高翔所著《视觉slam14讲》的内容总结，文中的主要文字和代码、图片都是引用自课本和高翔博士的博客。代码运行效果是在自己电脑上实际运行得出。手动记录主要是为了深入理解
涉及到的主要内容如下

• 理解Pose Graph 优化
• 因子图优化
• 增量式图优化

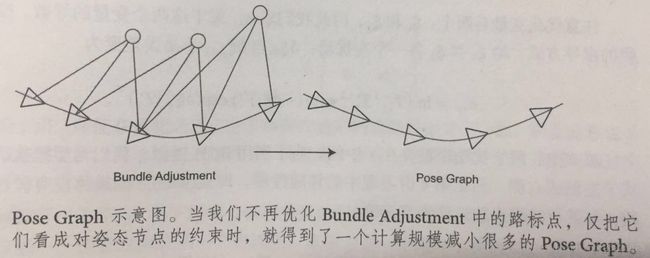
1 位姿图(Pose Graph)

1.1 Pose Graph的意义

带有相机位姿和空间点的优化称为BA优化，可以求解大规模定位和建图的问题。但是随着机器人运动轨迹变长，地图规模变大，BA的计算效率会降低。
实际上，通过若干次的观测之后，收敛的特征点，空间位置会收敛到一个固定值，而发散的点则观测不到了。
因此，倾向于在优化几次后就把特征点固定住，只把他们看做位姿估计的约束，不再实际优化他们的位置估计。

可以构建一个只有轨迹的图优化，而位姿节点之间的边，由关键帧之间通过特征匹配之后得到的运动估计来给定初始值。不同的是，初始估计完成后就不再优化那些路标点的位置，而只关心所有相机位姿之间的关系。

1.2 Pose Graph优化推导

Pose Graph节点表示相机位姿，用 ξ1,...,ξn 表达，边是两个位姿节点之间的相对运动估计，这种估计可能来自于特征点法或者直接法，称 ξi和ξj 之间运动为 △ξij 。

△ξij=ξ−1i。ξj=ln(exp((−ξi)^)exp(ξ^j))∨

构建误差

eij=ln(exp((−ξij)^)exp((−ξi)^)exp(ξ^j))∨

优化变量有两个 ξi和ξj ，最终的总体目标函数为

minξ=12∑i,j∈εeTi,j∑i,j−1ei,j

接下来用高斯牛顿法、列文伯格——马夸特方法求解此问题。

2 因子图优化

2.1 贝叶斯网络Bayes Network

从贝叶斯网络的角度来看，SLAM可以表达成一个动态的贝叶斯网络(Dynamic Bayes Network,DBN)。贝叶斯网络是一种概率图，由随机变量节点和表达随机变量条件独立性的边组成，形成一个有向无环图。

通过这种方式，构建一个贝叶斯网络，表达了所有的变量，以及各个方程给出的变量之间的条件概率关系。后端优化的目标就是在这些约束下，通过调整贝叶斯网络中随机变量的值，是的后验概率达到最大。

{x,l}∗=arg max(x0)∏P(xk|xk−1,μk)∏P(zk|xi,lj)

这样一个由条件概率描述的贝叶斯网络，可以使用概率图模型中的算法进行求解。进一步观察发现后验概率由多项因子成绩组成，因此贝叶斯网络又可以转换为一个因子图(Factor Graph)

2.2 因子图

因子图是无向图，由两种节点组成，表示优化变量的节点和表示因子的因子节点。

运动方程和观测方程作为因子存于图中。因为可能表达成概率分布的信息有许多种，于是因子图也可以定义成许多不同的因子。比如轮式编码器的测量、IMU的测量，使之成为一种非常通用的优化方式。

2.3 增量特性

从优化的角度来讲，优化一个因子图和普通的图并没有太大区别——因为最后都是解决一个最小二乘问题，不断寻找梯度，使目标函数下降。因子图优化的稀疏性与凸优化类似，通过稀疏QR分解、Schur补或者Cholesky分解，加速对因子图优化的求解。
Kaess等人提出的iSAM(incremental Smooth and Mapping)中，对因子图进行了更加精细的处理，使得它可以增量式的处理后端优化。
调整目标函数

J(x)=∑keTv,kR−1kev,k+∑k∑jeTy,k,jQ−1k,jey,k,j

中的优化变量，使目标函数下降。无论采用哪种梯度下降策略，最后碰到一个形如

H△x=g

的线性方程求解。

3 后端优化代码实践

原生位姿图如下

3.1 使用g2o/types/slam3d/中的SE3表示位姿图

它实质上是四元数而非李代数，效果图如下

代码运行结果

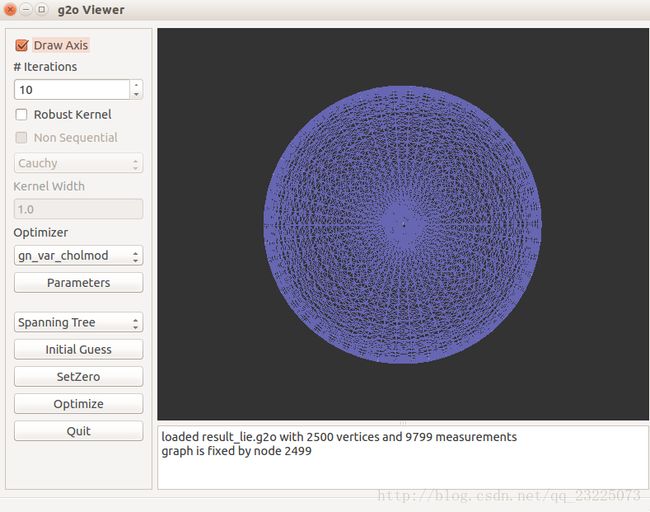
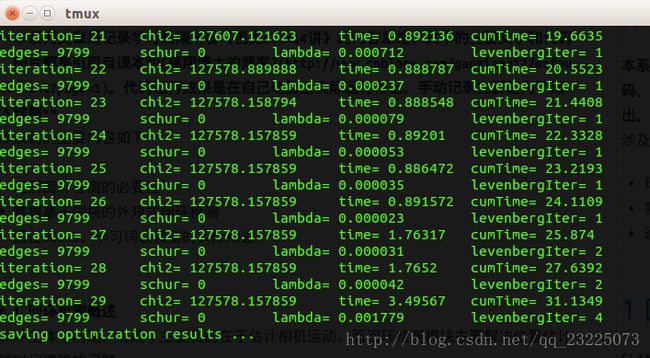
3.2 使用李代数表达位姿图

代码运行结果

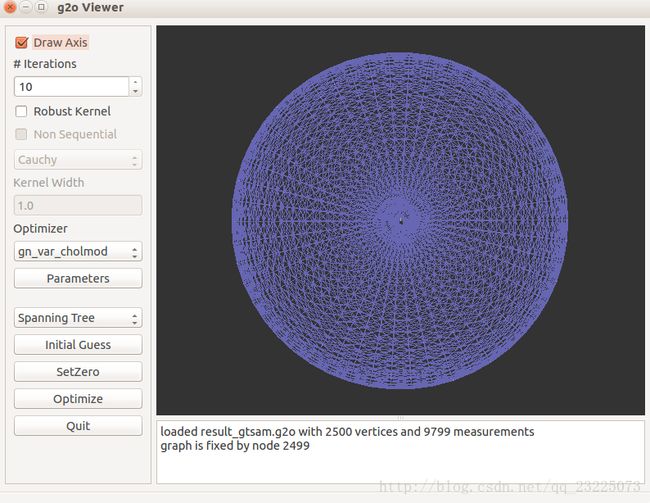
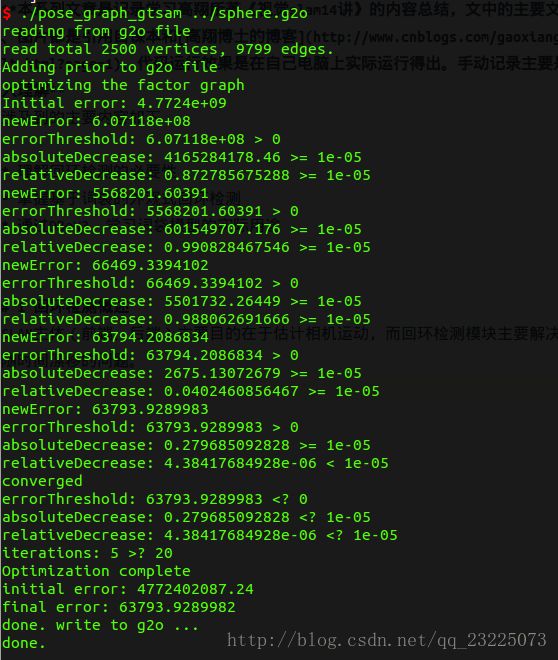
3.3 使用gtsam 中的因子图表达位姿图

代码运行结果

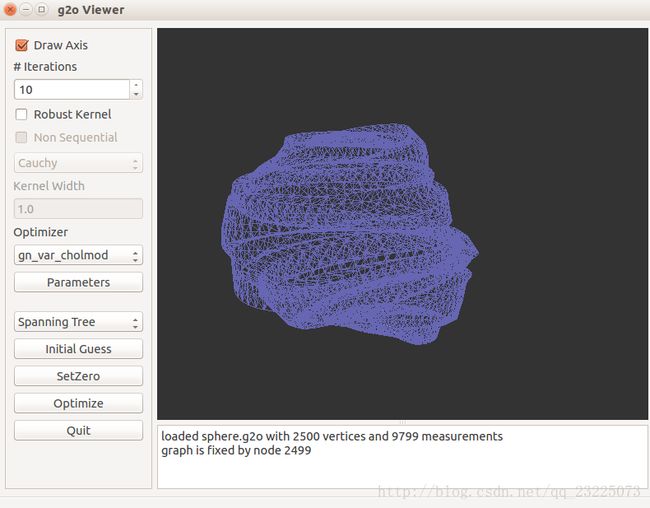
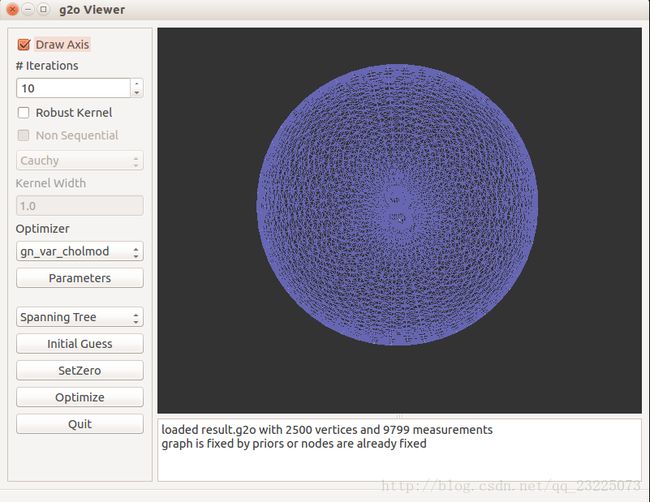
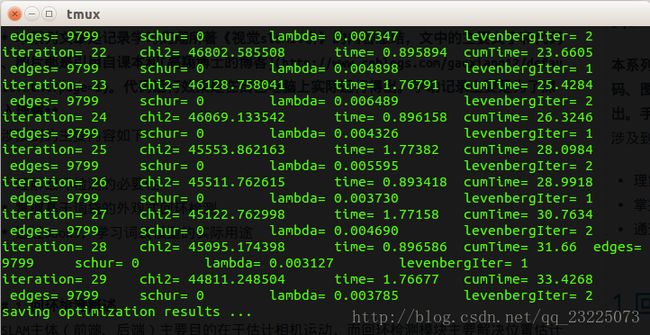
3.4 总结

以上三种优化都使得从一个不规则的形状优化成了一个看起来完整的球。从程序迭代次数的角度来比较可以看出前两种相差不大，但是使用李代数优化可以在相对较少的迭代次数下得到更好的结果，第三种方法使用因子图优化在得到误差相近的结果是迭代次数最少。