问题1 机器学习篇 如何解决过拟合(overfiting)?
向自己提问题是一个很好的学习方式。
问题: 如何解决过拟合(overfiting)?
在解决这个问题之前先明确问题是什么.这涉及到另外一些问题,什么是过拟合?过拟合与什么因素有关?等等
答:
1)直观理解过拟合
先说说经验误差,学习器在训练集上的预测值和真实值之间的差异称为经验误差。我们希望经验误差越小越好,但是当经验误差太小,以至于精确度约为100%时,我们就怀疑这个模型出现了过拟合。
所谓的过拟合就是学习器从数据中学得太多,已经把训练样本的某一些特点当作是所有潜在样本都会具有的一般性质。
2)从数学上理解过拟合
在监督学习中,我们所说的模型实际上是一个决策函数,对于给定的输入X,函数给出预测值f(X), f(X) f ( X ) 与真实值可能一致也可能不一致,通常使用损失函数(loss function)或者代价函数(cost function)来 衡量预测错误的程度,记为 L(Y,f(X)) L ( Y , f ( X ) ) 。常用的的损失函数有一下几种:

如果我们把输入和输出都看做随机变量,那么这两个随机变量会有联合分布P(X,Y), 考虑其损失函数的期望, 即平均意义下的损失,也称为风险函数或者期望损失:
实际中我们并不能得到期望损失,因为我们不知道联合分布。
我们总是训练模型,用模型的经验损失去近似期望损失。经验损失是模型上训练集的平均损失,表示为
只有在数据量大的时候,使用模型的经验损失去近似期望损失才会比较理想,当数据量小的时候,这个近似并不理想。
解决办法是经验风险最小化和结构风险最小化策略。
经验风险最小化可以使用下式表示:
极大似然估计是经验风险最小的一个例子。
使用经验风险最小策略的问题: 当样本不足或者很小时,经验风险最小化学习的效果不一定好,会产生过拟合。
这里从另外一个角度理解什么是过拟合。
3) 解决方法:
防止过拟合的方法就是使结构风险最小化,等价于正则化。
结构风险是在经验风险上加上表示模型复杂度的正则化或者罚项,如下式:
模型越复杂,复杂度 J(f) J ( f ) 越大,反之越小。复杂度表示对模型的惩罚。
λ≥0 λ ≥ 0 用于衡量经验风险和模型复杂度。
这个策略认为结构风险最小的模型是最优模型,从而把监督学习问题变成了经验风险函数或者结构风险函数的最优化问题。
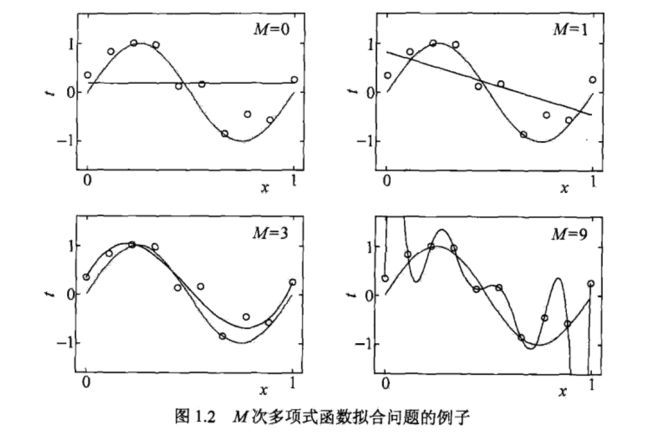
4)一个多项式拟合问题
我们会发现当M=9时,没有任何误差,已经过拟合。
5) one more thing
李航的书中还提到模型复杂度和预测误差的关系,这也涉及到泛化能力的问题。
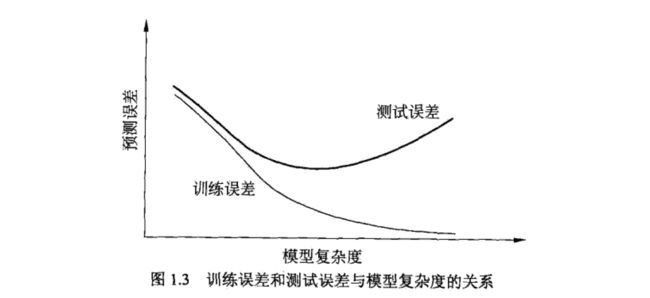
更进一步,什么是欠拟合?如何解决欠拟合?
参考:
周志华《机器学习》
李航《统计学习方法》