机器学习算法(3)——FM(Factorization Machine)算法(推导与实现)
1、前言
由于逻辑回归只能处理线性可分的模型或者数据集,又由于现实生活中的分类问题是多种多样的,存在大量的非线性可分的分类问题,为了能够满足要求,对逻辑回归(Logistic Regression)进行了如下的优化:
(1)、对特征进行处理:
如:核函数的方法,将非线性可分的问题转换成近似线性可分的问题;
(2)、对逻辑回归(Logistic Regression)进行扩展:
如:因子分解机 FM 算法就是对逻辑回归(Logistic Regression)的扩展。
2、因子分解机 FM(Factorization Machine) 模型
2.1、FM 算法模型的建立
对于因子分解机 FM 模型,引入度的概念。对于度为 2 的因子分解机模型为:
其中:w_0 为R,W为R^n,v属于R^(n,k);
上式中:Vi 表示的是系数矩阵 V 的第 i 维的向量,且Vi为:
|
|
k 为超参数,且 k 的大小称为 FM 算法模型的度,在因子分解机 FM 模型中,前两部分就是传统的线性模型,最后的那部分将两个互异的特征向量之间的相互关系考虑进去。
2.2、因子分解机 FM 算法可以处理的问题
(1)、回归问题(Regression)
(2)、二分类问题(Binary Classification)
(3)、排序(Ranking)
本文只讨论分类的问题,对于二分类问题,去阈值函数为 Sigmoid 函数:
同时,损失函数定义为:
2.3、FM算法中的交叉项系数
在基本线性回归模型的基础上引入交叉项:
这种直接在交叉项 x_i,x_j 的前面加上交叉系数 w_ij 的方式,在稀疏数据的情况下存在很大的缺陷,即在对于观察样本中未出现交互的特征分量时,不能对相应的参数进行估计。
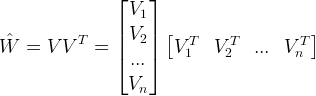
对每个特征分量 x_i 引入辅助向量 Vi=(v_i1,v_i2, ..., v_ik)利用 ViVj^T 对交叉项的系数 w_ij 进行估计,即:
|
|
令:
| |
于是有:
这样对应了一种矩阵的分解,对 k 值的限定、FM 的表达能力均有一定的影响。
2.4、FM 模型交叉项参数的求解详细推导
对于交叉项的求解可以效仿如下:
2.5、用随机梯度法对 FM 模型参数求解
假设数据集 X 中有 m 个训练样本,即
同时每个样本对应一个特征X^(i):
对于度 k=2 的因子分解机 FM 模型来说,其主要的参数就一次项和常数项的参数 w0,w1....,wn 以及交叉系数矩阵 V ,在利用随机梯度对模型的参数进行学习的过程中,主要是对损失函数 loss 的求导。
| |
而:
| |
2.6、FM 算法的流程
(1)、初始化权重 w0,w1,...,wn 和 v系数矩阵;
(2)、对每个样本:
![]()
对于特征 i:
![]()
对于“ 度 f—>k ”:
(3)、重复步骤(2),直到满足条件停止。
3、Python 实现 FM 算法
3.1、初始化参数
# 初始化权重 w 和交叉项权重 v
def initialize_w_v(n, k):
w = np.ones((n, 1))
v = np.mat(np.zeros((n, k)))
for i in range(n):
for j in range(k):
v[i, j] = np.random.normal(0, 0.2) # 把 v 中的值变为服从 N(0, 0.2) 正态分布的数值
return w, v3.2、损失函数的实现
# 定义误差损失函数 loss(y', y) = ∑-ln[sigmoid(y'* y)]
def get_cost(predict, classLabels):
m = np.shape(predict)[0]
# m = len(predict)
cost = []
error = 0.0
for i in range(m):
error -= np.log(sigmoid(predict[i] * classLabels[i]))
cost.append(error)
return error3.3、梯度下降法训练模型 Python 代码实现
# 用梯度下降法求解模型参数,训练 FM 模型。
def stocGradient(dataMatrix, classLabels, k, max_iter, alpha):
"""
:param dataMatrix: 输入的数据集特征
:param classLabels: 特征对应的标签
:param k: 交叉项矩阵的维度
:param max_iter: 最大迭代次数
:param alpha: 学习率
:return:
"""
m, n = np.shape(dataMatrix)
w0 = 0
w, v = initialize_w_v(n, k) # 初始化参数
for it in range(max_iter):
# print('第 %d 次迭代' % it)
for x in range(m):
v_1 = dataMatrix[x] * v # dataMatrix[x]的 shape 为(1,n),v的 shape 为(n,k)--->v_1的 shape为(1, k)
v_2 = np.multiply(dataMatrix[x], dataMatrix[x]) * np.multiply(v, v)
interaction = 0.5 * np.sum(np.multiply(v_1, v_1) - v_2)
p = w0 + dataMatrix[x] * w + interaction
loss = sigmoid(classLabels[x] * p[0, 0]) - 1
w0 = w0 - alpha * loss * classLabels[x]
for i in range(n):
if dataMatrix[x, i] != 0:
w[i, 0] = w[i, 0] - alpha * loss * classLabels[x] * dataMatrix[x, i]
for j in range(k):
v[i, j] = v[i, j] * alpha * loss * classLabels[x] * (dataMatrix[x, i] * v_1[0, j] - v[i, j] *
dataMatrix[x, i]*dataMatrix[x, i])
if it % 1000 == 0:
print("\t迭代次数:" + str(it) + ",误差:" + str(get_cost(prediction(np.mat(dataMatrix), w0, w, v), classLabels)))
return w0, w, v3.4、FM 算法的完整 Python 代码
# -*- coding: utf-8 -*-
# @Time : 2019-1-11 13:59
# @Author : Chaucer_Gxm
# @Email : [email protected]
# @File : Train.py
# @GitHub : https://github.com/Chaucergit/Code-and-Algorithm
# @blog : https://blog.csdn.net/qq_24819773
# @Software: PyCharm
import numpy as np
import time
# 导入准备训练的数据集
def load_data(filename):
data = open(filename)
feature = []
label = []
for line in data.readlines():
feature_tmp = []
lines = line.strip().split('\t')
for x in range(len(lines)-1):
feature_tmp.append(float(lines[x]))
label.append(int(lines[-1])*2-1)
feature.append(feature_tmp)
data.close()
return feature, label
# 初始化权重 w 和交叉项权重 v
def initialize_w_v(n, k):
w = np.ones((n, 1))
v = np.mat(np.zeros((n, k)))
for i in range(n):
for j in range(k):
v[i, j] = np.random.normal(0, 0.2) # 把 v 中的值变为服从 N(0, 0.2) 正态分布的数值
return w, v
# 定义 Sigmoid 函数
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# 定义误差损失函数 loss(y', y) = ∑-ln[sigmoid(y'* y)]
def get_cost(predict, classLabels):
m = np.shape(predict)[0]
# m = len(predict)
cost = []
error = 0.0
for i in range(m):
error -= np.log(sigmoid(predict[i] * classLabels[i]))
cost.append(error)
return error
# 用梯度下降法求解模型参数,训练 FM 模型。
def stocGradient(dataMatrix, classLabels, k, max_iter, alpha):
"""
:param dataMatrix: 输入的数据集特征
:param classLabels: 特征对应的标签
:param k: 交叉项矩阵的维度
:param max_iter: 最大迭代次数
:param alpha: 学习率
:return:
"""
m, n = np.shape(dataMatrix)
w0 = 0
w, v = initialize_w_v(n, k) # 初始化参数
for it in range(max_iter):
# print('第 %d 次迭代' % it)
for x in range(m):
v_1 = dataMatrix[x] * v # dataMatrix[x]的 shape 为(1,n),v的 shape 为(n,k)--->v_1的 shape为(1, k)
v_2 = np.multiply(dataMatrix[x], dataMatrix[x]) * np.multiply(v, v)
interaction = 0.5 * np.sum(np.multiply(v_1, v_1) - v_2)
p = w0 + dataMatrix[x] * w + interaction
loss = sigmoid(classLabels[x] * p[0, 0]) - 1
w0 = w0 - alpha * loss * classLabels[x]
for i in range(n):
if dataMatrix[x, i] != 0:
w[i, 0] = w[i, 0] - alpha * loss * classLabels[x] * dataMatrix[x, i]
for j in range(k):
v[i, j] = v[i, j] * alpha * loss * classLabels[x] * (dataMatrix[x, i] * v_1[0, j] - v[i, j] *
dataMatrix[x, i]*dataMatrix[x, i])
if it % 1000 == 0:
print("\t迭代次数:" + str(it) + ",误差:" + str(get_cost(prediction(np.mat(dataMatrix), w0, w, v), classLabels)))
return w0, w, v
# 定义预测结果的函数
def prediction(dataMatrix, w0, w, v):
m = np.shape(dataMatrix)[0]
result = []
for x in range(m):
inter_1 = dataMatrix[x] * v
inter_2 = np.multiply(dataMatrix[x], dataMatrix[x]) * np.multiply(v, v)
interaction = 0.5 * np.sum(np.multiply(inter_1, inter_1) - inter_2)
p = w0 + dataMatrix[x] * w + interaction
pre = sigmoid(p[0, 0])
result.append(pre)
return result
# 计算准确度
def getaccuracy(predict, classLabels):
m = np.shape(predict)[0]
allItem = 0
error = 0
for i in range(m):
allItem += 1
if float(predict[i]) < 0.5 and classLabels[i] == 1.0:
error += 1
elif float(predict[i]) >= 0.5 and classLabels[i] == -1.0:
error += 1
else:
continue
return float(error)/allItem
# 保存模型的参数
def save_model(filename, w0, w, v):
f = open(filename, 'w')
f.write(str(w0)+'\n')
w_array = []
m = np.shape(w)[0]
for i in range(m):
w_array.append(str(w[i, 0]))
f.write('\t'.join(w_array)+'\n')
m1, n1 = np.shape(v)
for i in range(m1):
v_tmp = []
for j in range(n1):
v_tmp.append(str(v[i, j]))
f.write('\t'.join(v_tmp)+'\n')
f.close()
# 主函数
def main():
# 第一步:导入数据
feature, label = load_data('train_data.txt')
# print(feature, label)
# 第二步:利用梯度下降训练模型
w0, w, v = stocGradient(np.mat(feature), label, 4, 20001, 0.02)
predict_result = prediction(np.mat(feature), w0, w, v)
print('训练精度为:%f' % (1-getaccuracy(predict_result, label)))
# 第三步保存模型
save_model('weights_FM', w0, w, v)
if __name__ == '__main__':
start = time.time()
main()
end = time.time()
print('训练模型用时为:%s' % str(end-start))
训练结果:
21.660687655417806
1.2649489467261146 75.27079468117786
-0.0 -0.0 -0.0 -0.0
0.0 0.0 0.0 0.0
测试结果:
0.9989796253213139
0.9999443493345659
0.623877247116008
0.9994974000340888
0.9999892853562842
0.9117533237892267
0.9993122746939441
0.9999998391255357
0.9518803708612011
0.9518180046166856
0.999999939840248完整程序(训练程序+测试程序)与数据集地址:
https://github.com/Chaucergit/Code-and-Algorithm/tree/master/ML/3.Factorization%20Machine
参考书目:
[1].统计方法.李航
[2].Python机器学习算法.赵志勇
[3].利用Python进行数据分析.WesKinney著,唐学韬等译

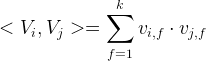
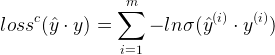
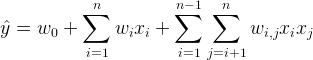

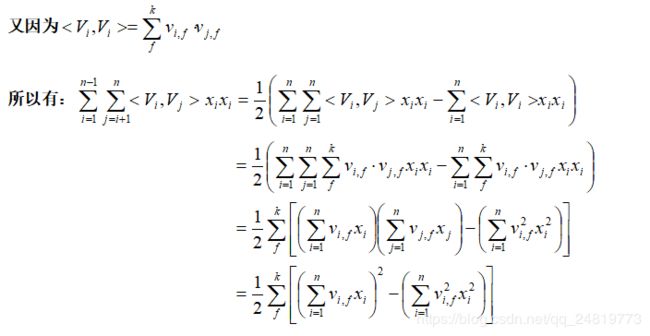
![\large v_{i,f}=:v_{i,f}-\alpha[1-\partial(\hat{y}\cdot y)]\cdot y \cdot[x_i\sum_{j=1}^{n}v_{j,f}x_j-v_{i,f}x_i^2]](http://img.e-com-net.com/image/info8/138fea62a346463b875e1134a902e5c8.gif)