逻辑回归及模型评估
本文通过逻辑回归分类来预测一个学生是否被录取,来熟悉python逻辑回归模型及模型的评估,数据集有需要的可以联系我qq:1344184686。
一、读入数据
#1、【读入数据】
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
#gpa为绩点,gre为一种英语等级考试
data = pd.read_csv('admissions.csv')
data.head()读入结果如下所示:
熟悉一下sigmoid函数:
#2、【sigmoid函数】
def sigmoid(z):
h = 1/(1+np.exp(-z))
return h
z = np.linspace(-5,5,40)
h = sigmoid(z)
plt.plot(z,h)sigmoid函数图像如下图:
二、选择模型,训练并预测
#3、【用验证集测试】
from sklearn.linear_model import LogisticRegression
model = LogisticRegression()
model.fit(data[['gpa']],data[['admit']])#为方便可视化展示,这里用一个特征进行训练
predict_proba = model.predict_proba(data[['gpa']])#两类的概率性,两列,第一列为取0的概率,第二列为取1的概率
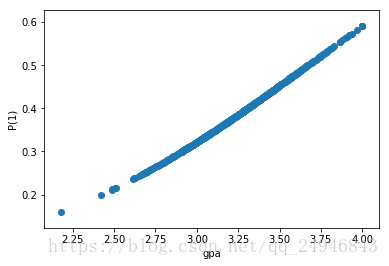
plt.scatter(data['gpa'],predict_proba[:,1])
plt.xlabel('gpa')
plt.ylabel('P(1)')
plt.show()
prediction = model.predict(data[['gpa']])#分类
plt.scatter(data['gpa'],prediction)
plt.xlabel('gpa')
plt.ylabel('label')
plt.show()预测结果如下,可见'gpa'即绩点越高,被录取的概率越大:
三、模型评估
很多时候,用精度来评判模型的好坏不准,比如说1000个人990个正常人为正例,10个人癌症为负例,现用模型预测后得到1000个人都正常,则精度达到99%,实际上这模型根本没用,因为一个癌症患者都检测不出,所以很多情况下,精度是会骗人的。这里用检测正例的效果tpr和检测负例的效果fpr以及检测正例负例的综合效果roc曲线来评估模型。
#4、【模型评估】
#精度即预测对的正例个数除以总数
from sklearn.metrics import accuracy_score
score = accuracy_score(data['admit'],prediction)
print(score)
#TP:true positive即预测对了为正例;
#FN:false negative即预测错了为负例,说明其原来真实值为正例
#TN:true negative即预测对了为负例
#FP:false positive即预测错了为正例
#模型预测正例的效果用tpr = TP/(TP+FN),即预测对了为正例的数量除以总的正例数量
true_positive_filter = (data['admit']==1) & (prediction==1)
true_positive = len(data[true_positive_filter])
print(true_positive)
false_negative_filter = (data['admit']==1) & (prediction==0)
false_negative = len(data[false_negative_filter])
print(false_negative)
#模型预测负例的效果用fpr = TN/(TN+FP)
true_negative_filter = (data['admit']==0) & (prediction==0)
true_negative = len(data[true_negative_filter])
print(true_negative)
false_positive_filter = (data['admit']==0) & (prediction==1)
false_positive = len(data[false_positive_filter])
print(false_positive)
#tpr = 0.127说明假设现在有一百个人应该被录取,你的模型只让约12个人录取,剩余88个人不让录取
#可看到刚才精度达到64.6%,而检测正例的效果才达到12.7%,所以以后评估模型不能只简单的看精度
tpr = true_positive/(true_positive + false_negative)
print(tpr)
fpr = true_negative/(true_negative + false_positive)
print(fpr)
####运行结果如下:
0.6459627329192547
31
213
385
15
0.12704918032786885
0.9625
上面为了方便是直接拿训练集进行测试,下面改用测试集进行测试。
#5、【用测试集测试】
#首先对原始数据进行洗牌,原始数据是按标签值排序的,前面都是标签0的数据,后面都是标签为1的数据,一定要记得洗牌,不然你直接拿前面数据训练,前面数据都是0类,根本分不了类。
shuffle_index = np.random.permutation(data.index)
#print(shuffle_index)
shuffle_data = data.iloc[shuffle_index]
#也可以from sklearn.model_selection import
#train_test_split(train_data,train_label,test_size)来分割数据
#即将训练集进行切割用来交叉验证
train = shuffle_data.iloc[0:500]
test = shuffle_data.iloc[500:len(shuffle_data)]
model = LogisticRegression()
model.fit(train[['gpa']],train['admit'])
prediction = model.predict(test[['gpa']])
accuracy_score(test['admit'],prediction)
####运行结果如下:
0.6875ROC曲线:前面根据定义计算fpr,tpr,可以直接用sklearn.metrics包里的roc_curve来计算,roc_curve里面第一个参数为测试集的标签,第二个参数为取正例的概率,返回值为fpr检测负例的效果,tpr检测正例的效果,threshold系统通过设定不同的阈值来分类,即概率性大于阈值的取1,小于阈值的取0。
from sklearn.metrics import roc_curve
predict_prob = model.predict_proba(test[['gpa']])
fpr,tpr,threshold = roc_curve(test['admit'],predict_prob[:,1])
#print(threshold)
plt.figure(figsize=(10,10))
plt.plot(fpr,tpr)
plt.show()
#roc曲线与x轴围成的面积,即其积分,代表模型检测正例和负例的综合效果
from sklearn.metrics import roc_auc_score
score = roc_auc_score(test['admit'],predict_prob[:,1])
print(score)roc曲线如下:
交叉验证:一来如果你拿到的测试集正好是噪音点或者说比较差的数据,拿来测试模型会很差,可能就将该模型舍弃掉了,而实际上该模型很好,为了改善这种情况,对训练集进行交叉验证取平均。二来拿神经网络模型来说,会将训练集拆分成训练集和验证集,边训练时边拿验证集来验证,当验证集的误差连续k次变大,就停止训练,提高模型的泛化能力,如果将训练集全部拿来训练一直迭代,很可能会造成过拟合。
#9、交叉验证
from sklearn.cross_validation import KFold
from sklearn.cross_validation import cross_val_score
data = pd.read_csv('admissions.csv')
train_data = data.drop(data['admit'])
kf = KFold(len(train_data),5,shuffle=True)
model = LogisticRegression()
#可以通过scoring指定是求精度值accuracy还是roc_auc
accuracies = cross_val_score(model,train_data[['gpa']],train_data['admit'],scoring = 'accuracy',cv = kf)
average_accuracies = accuracies.mean()
print(accuracies)
print(average_accuracies)
####运行结果如下:
[0.60465116 0.66666667 0.7109375 0.6484375 0.6171875 ]
0.6495760658914729