强化学习(RLAI)读书笔记第六章差分学习(TD-learning)
第六章:Temporal-Difference Learning
TD-learning算法是强化学习中一个独具特色而又核心的想法,结合了蒙特卡洛算法和动态规划的想法。和MC一样不需要环境模型直接从sample里学习,也像DP一样使用bootstrap通过别的状态值的估计更新当前状态值。首先也关注的是给定策略进行prediction或者叫policy evaluation。对于control(找到最优策略)的问题,DP,TD和MC都用的是GPI的框架,主要的区别在prediction的时候。
6.1 TD Prediction
TD和MC算法都使用经验来解决prediction的问题。给定一个策略![]() 决策下的一些经验序列,两个方法都为出现在序列里的非中止状态更新值函数V。大致上说,MC方法需要等到一个状态后面所有的反馈都知道,把这个return作为值函数V的目标。简单的一个非稳态环境的every-visit方法的更新为
决策下的一些经验序列,两个方法都为出现在序列里的非中止状态更新值函数V。大致上说,MC方法需要等到一个状态后面所有的反馈都知道,把这个return作为值函数V的目标。简单的一个非稳态环境的every-visit方法的更新为![]() 。这种方法叫做常数
。这种方法叫做常数![]() MC。MC需要等待一个序列到达重点才能更新V,而TD方法只需要等待下一步完成。最简单的TD方法更新为
MC。MC需要等待一个序列到达重点才能更新V,而TD方法只需要等待下一步完成。最简单的TD方法更新为
![]()
在MC方法中目标值是![]() 而这里是
而这里是![]() ,这种方法叫做TD(0),也叫一步TD法。
,这种方法叫做TD(0),也叫一步TD法。
 TD方法中的估计值在两个方面,一个是其是对期望值的一个采样,第二是它使用了当前的V值进行计算而不是
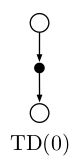
TD方法中的估计值在两个方面,一个是其是对期望值的一个采样,第二是它使用了当前的V值进行计算而不是![]() 。所以TD结合了MC中的采样法和DP的boostrapping。表格型TD(0)算法的backup diagrams如右图。TD法和MC法被叫做sample updates是因为它们都往后进行了状态的采样,并且将后面状态的值函数和反馈用来更新当前值函数。sample updates和DP算法的期望更新不同,因为它基于对后面状态的单个采样而不是基于所有状态的分布。
。所以TD结合了MC中的采样法和DP的boostrapping。表格型TD(0)算法的backup diagrams如右图。TD法和MC法被叫做sample updates是因为它们都往后进行了状态的采样,并且将后面状态的值函数和反馈用来更新当前值函数。sample updates和DP算法的期望更新不同,因为它基于对后面状态的单个采样而不是基于所有状态的分布。
最后要提到TD算法更新时括号里的部分可以被认为是一种用来评估当前状态值函数和更好的估计值![]() 之间的误差。这个值叫做TD error,在强化学习算法中以各种形式出现。
之间的误差。这个值叫做TD error,在强化学习算法中以各种形式出现。
练习6.1
练习6.2 TD算法在到达新建筑的时候就可以根据以往经验v中从下一个位置parking lot的值进行预测,而MC需要经历从头到尾的遍历而且前几次的预测方差会很大。
6.2 Advantages of TD Prediction Methods
首先TD算法相比于DP算法的一个优势就是不需要环境模型,也就是下一状态的反馈和状态分布。而TD相比于MC算法的最明显的优势是TD可以很自然的作为一种在线的全增量的方式计算。MC必须等到一个episode结束以后才可以进行计算,而有些episode很长,有些episode是无法走到中止状态的。TD算法就可以直接在每一个状态转移之间进行学习。
同时,TD(0)算法在保证步长是足够小的常数或者步长根据2.7收敛条件不断缩小的情况下是保证收敛的。而且TD法和MC算法都可以进行异步更新并且保证收敛。虽然没有数学证明但是实践中往往TD算法收敛的更快。
练习6.3 0.45
练习6.4 不会变化。TD算法的趋势是步长越小收敛越慢但相对方差会更小,而MC是步长越大,最后方差越大而收敛速度变化不明显。
练习6.5 TD算法本身会造成一定的偏差
练习6.6 1.直接解方程组 2.线性规划 3. policy evaluation 直接解
6.3 Optimality of TD(0)
如果只有有限数量的episode作为训练样本,那么这些样本会被重复训练直到值函数收敛。而这些样本在用来更新值函数的时候,每个转换过程的都会多次计算相应增量式更新公式中的的error,但是值函数只会用这些error的和更新一次。每一个时间t的值函数更新了之后会对下一个状态的值函数进行相同的计算直到所有的状态都达到收敛。这种方式叫做batch updating因为所有的更新只有在处理完每一个batch的训练数据之后才会进行。
只要步长设置的足够小,那么在batch updating下的TD(0)算法都会确定性的收敛至一个和步长无关的值。常数步长的MC算法也会同样收敛,但收敛到不同的值上。在普通的更新方式下,两个算法并不是直接朝着各自收敛值而去,但是某种程度上也是朝着这个方向进行。
书中的例子表明了这两个算法估算值的区别。batchMC算法总是收敛至一个在训练集上最小方差的值,而batch TD(0)收敛到一个对于马尔科夫模型的最大似然模型最相符的值。一个参数的最大似然估计是指产生概率最大的值。这种方法的值叫做certainty-equivalence estimate因为这个值对于相应建立起的环境模型是完全正确的而非估计值。TD(0)算法就收敛到这个值。这也就解释了为什么TD(0)在实际中总是收敛得比MC算法更快,因为它是直接朝着certainty equivalence estimate的方向进行计算的。但是这个值却没有办法直接计算,相对来说TD(0)算法可能是唯一一个可行的计算这个值的算法。
练习6.7 ![]()
6.4 Sarsa: On-policy TD Control
现在考虑控制的问题。一般来说使用的都是GPI模型框架,只不过是使用了TD版本的评估方式。和MC算法中一样,需要考虑exploring和exploit以及使用on-policy 和 off-policy两种方式的算法。
首先我们计算状态动作对值函数Q而不是V。而对于on-policy的算法来说需要计算当前策略下每个状态动作对的值函数,也就是上节prediction的过程。之后考虑从一个状态动作对转移到另一个,这个都是在GPI框架下的MDP,理论保证收敛,更新公式如下:
![]()
这利用了![]() 这一个五元组,也就得到了Sarsa算法。算法的backup diagrams如右图。很自然想
这一个五元组,也就得到了Sarsa算法。算法的backup diagrams如右图。很自然想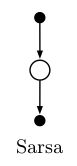 到用Sarsa prediction来进行一个on-policy的控制算法。作为一个on-policy的算法,我们进行评估算法的同时也使用同样的算法来进行决策,同时对算法进行改进。算法过程如图:
到用Sarsa prediction来进行一个on-policy的控制算法。作为一个on-policy的算法,我们进行评估算法的同时也使用同样的算法来进行决策,同时对算法进行改进。算法过程如图:
6.5 Q-learning: Off-policy TD Control
早期强化学习的一大突破就是一个off-policy的TD control算法叫做Q-learning,更新公式为
![]()
这个算法直接利用下一状态的最优值来估计当前状态动作对的值函数,而和当前遵守的策略无关。这很大程度的简化了算法的分析和促进了收敛证明。不过策略依然决定了选定那些状态动作对来进行更新,想要达到收敛就依然需要遍历所有的状态动作对。同样在这个假设下以及对步长参数的一些变化,Q-learning算法保证收敛至最优值q。
练习6.11 因为Q-learning算法正在遵循的策略和正在被评估的策略可能是两种不同的策略。
练习6.12 不一定,因为Sarsa在更新状态值之前选择动作,而Q-learning在更新当前状态动作值函数之后选择。这样有可能下一个状态和当前状态相同会导致选的动作不一样。
6.6 Expected Sarsa
考虑一个类似Q-learning的算法但是下一个状态的估计值从最大值改为期望值,也就是考虑紧当前策略下采取动作的概率。更新规则为
其它的部分都和Q-learning一样。对于给定下一状态,这个算法和Sarsa一样朝着其期望值的方向移动,所以这个算法叫做Expected Sarsa算法。算法增加了一定的计算量,但是减小了采取动作造成的方差。对于同样数量的样本,这个算法比Sarsa算法表现的更好一些。这个算法可以将步长设为1而不会降低性能,Sarsa算法就只能在比较小的步长下表现的好。
expected Sarsa算法也可以用为off-policy的形式,比如当行为策略是![]() -greedy而被评估的策略是贪婪算法,那么这个算法就是Q-learning算法。
-greedy而被评估的策略是贪婪算法,那么这个算法就是Q-learning算法。
6.7 Maximization Bias and Double Learning
目前讨论的control算法在构造目标策略的时候都使用了最大化。在这些算法中,评估值的最大值被用来隐式地表示最大值的估计,这可能会导致一个很严重的正偏差。比如单个状态s下有不同的动作a,每个动作a的值都是期望为0,但是有方差,因此有的动作的观察值大于0有的小于0。但是最大的估计值是正的,因此就有了一个正的偏差,叫做maximization bias。
一种看待这个问题的观点是说因为使用了同样的样本来决定最优的动作以及评估动作值。如果我们把样本分成两个集合,每个都估计一个独立的估计值![]() 和
和![]() 。可以使用其中一个值来决定最优动作即
。可以使用其中一个值来决定最优动作即![]() ,而另一个值来作为这个动作的值函数的估计即
,而另一个值来作为这个动作的值函数的估计即![]() 。这样这个评估值就是无偏的。需要注意虽然我们有两个估计值,但是每一次转移状态只更新一个值,所以只增加了一倍的内存消耗但没有增加计算量。这个double learning的方式可以很自然的拓展到完全的MDP算法中去。比如Double q-learning,算法伪代码如图:
。这样这个评估值就是无偏的。需要注意虽然我们有两个估计值,但是每一次转移状态只更新一个值,所以只增加了一倍的内存消耗但没有增加计算量。这个double learning的方式可以很自然的拓展到完全的MDP算法中去。比如Double q-learning,算法伪代码如图:
同样的Sarsa和Expected Sarsa也有double的版本。
练习6.13
6.8 Games, Afterstates, and Other Special Cases
目前讲述的都是通用的算法,但是显然总是有一些例外用一些特殊方法会更好。对于第一章中讲的tic-tac-toe游戏来说,使用TD算法得到的既不是状态值函数也不是动作值函数。传统的状态值函数是估算在当前状态采取动作以后会得到的反馈期望,但是在这个例子里估计的是agent采取了动作之后的状态值。把这个状态叫做afterstates,这些状态值函数叫afterstate value functions。Afterstate可以被用在那些我们知道一些环境的变化但不能完全建模的情况。
使用这种设计显然是更有效率的。因为有的不同的position在采取了动作之后可能变化到同样的结果状态。这样对于传统的状态值函数这两个状态是分开的,但是对于afterstate value function就能够发现他们是相等的。这个技术用在很多情境下,比如排队任务等等。本书中目前讲到的GPI和策略以及(afterstate)值函数都能够大致的应用上,也需要考虑选择on-policy和off-policy以及需要exploring等等。
6.9 Summary
本章介绍了一种新的学习算法,差分(TD)学习。同样分为prediction和control两个部分。TD算法是MC的替代品。两种算法都是用DP中总结的GPI收敛框架。也就是把策略和值函数以交互的方式朝着最优前进。GPI中两个过程,一个是prediction。另一个是根据当前值函数改进策略。可以根据是否是on-policy来区分TDcontrol算法。Sarsa算法是on-policy的,Q-learning算法是off-policy的,这里讲的expected Sarsa也是off-policy的。还有一种新的TD算法在13章中会讲。
这章讲的算法在强化学习里都很常用。这可能是因为它们的简单,可以是在线的形式,需要很少的计算量,直接和环境进行交互;可以基本上直接用一个等式来表示算法,也只需要很小的代码程序来完成算法。以后介绍的算法都会保持这章算法的核心:online处理experience和相对少的计算量,它们也都会用TD error。这张介绍的算法应该被叫做one-step,tabular,model-free TD算法。
最后本章介绍的TD算法都是在强化学习环境下的,但是TD法可以用的更加的广泛。比如预测金融信息,大选结果等等。只有当TD法不被限制在强化学习的框架里,它的思想才会被真正理解。



