Bit Vector算法
摘要:
该算法常用到包分类中,初次接触到bit vector算法是在对海量数据的处理。
设想我们有个很大的数据集,它的总体个数为400亿个数字,需要消除重复的数据,一种想当然的做法是,每次读取一部分,进行消重,如每次读取1000万个数据进行消重,这样我们就可以将40亿个数字分成400部分,将消重后的数据合并,然后进行进一步消重,这种做法显然需要的花费很大的时间开销。假设将所有数据都读取到内存中,发现至少需要几个G的内存才嫩容纳这么多数据。
Bit Vector解决方案:
我们构造一个位数组,在java中实际上是由byte数组实现的,在c中我们可以使用char数组代替。设bit vector的第一位对应数字1,第二位对应数字2,那么第N位对应数字N,当我们读入一个数据的时候,将对应位置为1。这样就能将所有的数据都读入到一个bit vector中,显然这种方案也有缺点,设想我们如果读入2个数据,一个是1,一个是1000000,那么bit vector的长度取决于最大数,所以,bit vector适用在数据长度均衡的情况下。
Bit Vector实现:
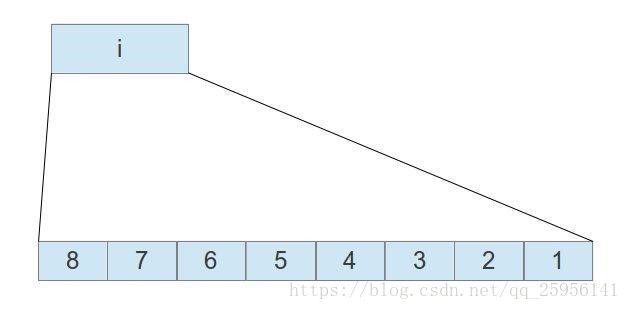
图1
如图1所示,假设i的1,那么i肯定映射在第一个byte中,若i是15,那么它将映射在第3个byte中,对于任意数据i,它将映射到下标为i/8向下取整再加1的byte数组中。
Bit vector实现函数:
Set(置位):对于读入的数据,将对应的bit位置为1。
Clear(清楚位):对于删除的数据,将对应的bit位置为0。
Get(读取位):读取某一位数据,结果是1则证明存在,为0则证明不存在。
Size(bit vector所能容纳的位个数):返回容器的长度。
Count(置位元素个数):返回所有被置为1的位的个数。
C代码实现(原文中没有提供C实现,以下为自己实现的代码):
typedef struct{
u8 * bits; //这里采用char代替java中的byte,考虑到兼容性,这里采用u8
int size;
int count;
}BitVector;
//初始化BitVector
void init(BitVector * bv,int size){
bv->size = size;
bv->bits = (u8 *)calloc(sizeof(u8),size>>3 + 1);
bv->count = 0;
}
void set(BitVector *bv,int data){
if(bv->bits[data>>3] & 1<<(data&7) == 0){
//由于下标从0开始,所以无需data>>3+1
bv->bits[data>>3] |= 1<<(data&7); //bit&7相当于截取后3位,等价于对8取余
bv->count ++;
}
}
void clear(BitVector * bv,int data){
if(bv->bits[data>>3] & 1<<(data&7) == 1<<(data&7)){
bv->bits[data>>3] &= ~(1<<(data&7));
bv->count --;
}
}
//返回1表示存在于bv,否则不存在于bv
int get(BitVector * bv,int data){
return (bv->bits[data>>3] & 1<<(data&7));
}
int getCount(BitVector * bv){
return bv->count;
}
原文java实现:
private byte[] bits;
private int size;
private int count = -1;
public BitVector(int n) {
size = n;
bits = new byte[(size >> 3) + 1];
}
public final void set(int bit) {
bits[bit >> 3] |= 1 << (bit & 7);
count = -1;
}
public final void clear(int bit) {
bits[bit >> 3] &= ~(1 << (bit & 7));
count = -1;
}
public final boolean get(int bit) {
return (bits[bit >> 3] & (1 << (bit & 7))) != 0;
}
/**
* 原文中没有在set和clear的时候进行count统计,所以它实现了一个getCount()函数
* 具体做法是遍历byte数组,由于每个byte数组中的1的取值可能只有0-255种,所以就
* 计算出byte数组中每个byte中1的个数,之后通过循环将整个byte数组的1的个数相
* 加即可。采用的是少量空间换时间的方案。对于每一种byte可能的取值的1的个数都进
* 行统计。在获取count不频繁的情况下,这种做法较为科学。
*/
private static final byte[] BYTE_COUNTS = { // table of bits/byte
0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
4, 5, 5, 6, 5, 6, 6, 7, 5, 6, 6, 7, 6, 7, 7, 8
};
public final int count() {
if (count == -1) {
int c = 0;
int end = bits.length;
for (int i = 0; i < end; i++)
c += BYTE_COUNTS[bits[i] & 0xFF]; // sum bits per byte
count = c;
}
return count;
}
原文地址:https://www.jianshu.com/p/2dbb88e2bfa9