机器学习中常见算法推导总结

本博客基于周志华老师《机器学习》、Ian Goodfellow《Deep Learning》、李航老师《统计学习方法》以及网上部分资料，为自己的学习笔记、总结以及备忘录，由于本人刚入门，欢迎大家指出错误。如有侵权，望告知，谢谢。

机器学习常见算法推导，主要以下几种算法：

knn、线性回归、逻辑回归、lda、感知机、bp、svm、em、pca

k近邻法（k-nearest neighbor，k-NN）:

    此处只讨论分类问题中的k近邻法。对于每一个训练实例点x，距离该点比其他点更近的所有点组成一个区域，叫做单元(cell)，每个训练实例点拥有一个单元，最近邻法将实例的类作为其单元中所有点的类标记。这样，每个单元的实例点的类别是确定的。对于测试样本而言，测试样本类别判定为测试样本最近的k个样本中最多类别。python给出了利用sklearn中的iris数据库进行knn分类的准确率结果，其中k=5。

import numpy as np
from sklearn import datasets,cross_validation

##load
def load_data():
    data=datasets.load_iris()
    return cross_validation.train_test_split(data.data,data.target,test_size=0.25,random_state=0)  
##knn
def knn(X_train,X_test,y_train,y_test,k):
    cnt=0;total_cnt=0
    m,n=np.shape(X_train)
    m0,n0=np.shape(X_test)
    for i in range(m0):
        dist=[]
        for j in range(m):
            distance=np.linalg.norm(X_test[i,:]-X_train[j,:])
            dist.append(distance)
        max_k=np.argsort(dist)[:k]
        index_y_test=[]
        for index in max_k:
            index_y_test.append(y_train[index])
        temp=0
        for p in index_y_test:
            count=index_y_test.count(p)
            if count>temp:
                temp=count
                index_predict=p
        y_predict=y_train[index_predict]
        if y_predict==y_test[i]:
            cnt+=1
        total_cnt+=1
    score=float(cnt/total_cnt)
    print('Score:%.2f'%score)
X_train,X_test,y_train,y_test=load_data()
knn(X_train,X_test,y_train,y_test,k=5)

线性回归（Linear Regression）:

    线性回归的基本想法是用一条直线尽可能地拟合数据，通过这条预测直线，尽可能准确地预测输出标记。具体的公式为：，其中，所有参数均为列向量。显然，我们的预期是尽可能地贴近真实的数值，由此，我们可以利用真实值与预测值的差值作为我们的损失函数。即。损失函数的选择还有很多种，在线性回归中选择MSE作为损失函数主要是基于其计算简单、可以凸优化。从令一种角度解释这个损失函数就是，测试集上个点到这条直线的距离平方和。显然，我们希望这个值越小越好。那么求解这条直线的问题就转化为求解损失函数最小化的问题。由于特征往往不止一个，所以对于一般的列向量而言，我们可以得到，可化为:（此处我们需要得出的其实考虑上了偏置，同样的在中我们也要加上一行1）。我们的目标是在给定的情况下，损失函数最小化，即求解最小值问题，由于损失函数本身为凸优化问题，所以极小值即为最小值。求解极小值时，我们通常令一阶导数为0，即,可以解出，其中必须保证矩阵可逆。若实际问题中矩阵不可逆，即可能由于特征数大于样本数，通常情况下是引入正则化。python给出了利用sklearn中diabets数据库进行线性回归的结果。

import numpy as np
from sklearn import datasets,cross_validation
##load
def load_data():
    data=datasets.load_diabetes()
    return cross_validation.train_test_split(data.data,data.target,test_size=0.25,random_state=0)
##linear
def linear_regression(*data):
    X_train,X_test,y_train,y_test=data
    m,n=np.shape(X_train)
    b=np.ones((m,1))
    X_train=np.hstack((X_train,b))
    m,n=np.shape(X_test)
    b=np.ones((m,1))
    X_test=np.hstack((X_test,b))
    y_train=y_train.reshape(-1,1)
    w=np.dot(np.dot(y_train.T,X_train),np.linalg.inv(np.dot(X_train.T,X_train)))
    y_predict=np.dot(w,X_test.T).reshape(-1,1)
    score=1-np.dot((y_predict-np.mean(y_test)).T,(y_predict-np.mean(y_test)))/np.dot((y_test-np.mean(y_test)).T,(y_test-np.mean(y_test)))
    print(score)
X_train,X_test,y_train,y_test=load_data()
linear_regression(X_train,X_test,y_train,y_test)

逻辑回归（Logistic Regression）:

    线性回归是利用线性模型进行回归学习，我们期望的是通过某种方法进行分类任务。所以我们期望找到一个单调可微函数分类任务的真实标记与线性回归模型的预测值联系起来。考虑二分类任务的话，我们利用sigmoid函数，将0.5作为阈值，大于0.5判为正类，小于0.5判为负类。同样对于逻辑回归而言，我们也有一个回归曲线，，其中。对于这个模型的损失函数，我们如果还采用MSE即均方误差的话，会发现不再是一个凸优化问题，这就导致我们求得的极值可能仅仅是极小值而不是最小值，由此，我们考虑新的损失函数，即极大似然。此时的损失函数为，，即，由此，采用梯度下降，（此处不考虑总样本），因此，权值的下降梯度为。python给出了利用随机梯度下降，sklearn中的breast_cancer数据集进行逻辑回归的结果。

import numpy as np 
from sklearn import datasets,cross_validation
##load
def load_data():
    data=datasets.load_breast_cancer()
    return cross_validation.train_test_split(data.data,data.target,test_size=0.25,random_state=0)
##logisitic
def sigmoid(x):
    return 1.0/(1+np.exp(-x))   
##predict
def predict(x):
    if x>=0.5:
        return 1
    else:
        return 0
def logistic(*data):
    X_train,X_test,y_train,y_test=data
    m,n=np.shape(X_train)
    b=np.ones((m,1))
    X_train=np.hstack((X_train,b))
    m,n=np.shape(X_test)
    b=np.ones((m,1))
    X_test=np.hstack((X_test,b))
    m,n=np.shape(X_train)
    y_train=y_train.reshape(-1,1).astype(float)
    theta=0.0005*np.random.random((n,1));alpha=0.001;max_cnt=500;cnt=0
    for i in range(max_cnt):
        h=sigmoid(np.dot(theta.T,X_train.T)).T##426*1
        error=y_train-h##426*1
        theta=theta+alpha*np.dot(X_train.T,error)
    h=sigmoid(np.dot(theta.T,X_test.T)).T
    y_predict=[]
    for i in h:
        y_predict.append(predict(i))
    n=len(y_predict)
    for i in range(n):
        if y_predict[i]==y_test[i]:
            cnt+=1
        else:
            pass
    score=float(cnt/n)
    print('Score:%.2f'%score)
X_train,X_test,y_train,y_test=load_data()
logistic(X_train,X_test,y_train,y_test)

LDA（Linear Discriminant Analysis）:

    线性判别分析的基本想法是，将我们需要分类的点投影在一条直线上，保证同类别的点距离最近，不同类别的点距离最远。

判断不同类别距离的方法是：先找出各类中心在直线上的投影点，然后利用L2范数。判断相同类别距离的方法是：将协方差矩阵投影在直线上（协方差：从物理意义上来讲，协方差表示了个向量之间的相关性，协方差为正值是正相关，负值是负相关，为0是不相关）。我们希望保证的是同类最近，异类最远，即各类中心最远，协方差最小。所以我们可以得到我们的最大化目标，即，令，，可得，，这就是我们想要最大化的目标。有广义瑞利商的性质可知，该函数的最大值是特征值的最大值，最小值是特征值的最小值。其中。所以，，即。利用sklearn中breast_cancer数据集，进行了lda判别。

import numpy as np
from sklearn import datasets,cross_validation

##load
def load_data():
    data=datasets.load_breast_cancer()
    X_train=data.data[:,:2]
    return cross_validation.train_test_split(X_train,data.target,test_size=0.25,random_state=0)
##lda
def lda(*data):
    X_train,X_test,y_train,y_test=data
    m=np.shape(y_train)[0]
    class_a=[];class_b=[];cnt=0
    for i in range(m):
        if y_train[i]==0:
            class_a.append(X_train[i])
        else:
            class_b.append(X_train[i])
    X_train_a=np.array(class_a)
    X_train_b=np.array(class_b)
    mu_a=np.mean(X_train_a,axis=0).T.reshape(-1,1)
    mu_b=np.mean(X_train_b,axis=0).T.reshape(-1,1)
    Sw=np.dot((X_train_a.T-mu_a),(X_train_a-mu_a.T))+np.dot((X_train_b.T-mu_b),(X_train_b-mu_b.T))
    w=np.dot(np.linalg.inv(Sw),mu_a-mu_b)
    y_predict=np.dot(X_test,w)
    y_a=np.dot(mu_a.T,w)
    y_b=np.dot(mu_b.T,w)
    n=np.shape(y_predict)[0]
    for i in range(n):
        dist_a=np.linalg.norm(y_predict[i]-y_a)
        dist_b=np.linalg.norm(y_predict[i]-y_b)
        if dist_a

感知机（perceptron）:

    感知机是二类分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别，取+1和-1，感知机对应于输入空间（特征空间）中将实例划分为正负两类的分离超平面，属于判别模型，感知机学习旨在求出将训练数据进行分类的分离超平面，为此，导入基于误分类的损失函数，我们期望误分类的点尽可能少，所以我们的目标就是损失函数最小化。这里采用的方法是随机梯度下降。，，，。这里采用的自定义的线性可分数据集

import numpy as np 
import matplotlib.pyplot as plt
from sklearn import datasets
##load
def load_data():
    X_train=np.array([[3,4,1,1,3,2.5,2],[3,3,1,0,2.5,2,1.5]])
    y_train=np.array([1,1,-1,-1,1,-1,-1]).reshape(-1,1)##8*1
    return X_train.T,y_train
##sign
def sign(x):
    if x>0:
        return 1
    else:
        return -1
##perceptron
def perceptron(*data):
    X_train,y_train=data
    m,n=np.shape(X_train)##569*2
    for i in range(m):
        if y_train[i]==0:
            y_train[i]=-1
        else:
            pass
    weights=np.random.random((n,1))
    b=0
    alpha=1
    y_predict=[]
    is_meet=False
    while not is_meet:
        count=0
        for j in range(m):
            predict=sign(np.dot(X_train[j],weights)+b)
            if predict*y_train[j]<0:
                weights=weights+alpha*y_train[j]*(X_train[j,:].reshape(-1,1))
                b=b+alpha*y_train[j]
                count+=1
        if count==0:
            is_meet=True
    for i in range(m):
        y_predict.append(sign(np.dot(X_train[i],weights)+b))
    #print(y_predict)
    return weights,b
##plot
def plot(X_train,y_train,weights,b):
    X_a=[];X_b=[]
    m=np.shape(y_train)[0]
    for i in range(m):
        if y_train[i]==-1:
            X_a.append(X_train[i])
        else:
            X_b.append(X_train[i])
    plt.scatter(np.array(X_a)[:,0],np.array(X_a)[:,1],c='r',marker='o')
    plt.scatter(np.array(X_b)[:,0],np.array(X_b)[:,1],c='g',marker='o')
    x=np.arange(1,4,0.1)
    y=-(weights[0]*x+b)/weights[1]
    plt.plot(x,y)
    plt.show()
X_train,y_train=load_data()
weights,b=perceptron(X_train,y_train)
plot(X_train,y_train,weights,b)

支持向量机（Support Vector Machine）：

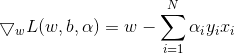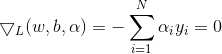    上一个感知机基于的是线性可分数据集，并且由于初值的选取比较随意，采用了随机梯度下降的方法，所以对于一个线性可分数据集通常会产生无数个划分超平面，这些超平面各有优劣。如果一个划分超平面距离我们划分的样本过近，很容易造成过拟合。所以，我们希望找到一个划分超平面，使其尽可能地远离样本点。从令一个角度来说，我们其实相当于给感知机加了一个正则化的系数。我们的目的是间隔最大化，即在 的条件下，最大化 ，即在此条件下，最小化 ，此为带约束问题，所以我们引入拉格朗日算子，定义拉格朗日函数 ，所以原问题转化为 求导可得 ， ，将两式带入可得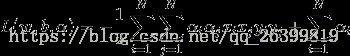， 求解其最大化问题，等价于求解 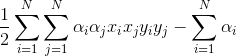最小值，在 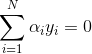的条件下。以下部分代码来源于《机器学习实战》。

import numpy as np
import matplotlib.pyplot as plt

def load_data():
    X_train=np.array([[3,4,1,1,3,2.5,2],[3,3,1,0,2.5,2,1.5]])
    y_train=np.array([1,1,-1,-1,1,-1,-1])
    return X_train,y_train

def selectJrand(i,m):
    j=i 
    while (j==i):
        j = int(np.random.uniform(0,m))
    return j

def clipAlpha(aj,H,L):
    if aj > H: 
        aj = H
    if L > aj:
        aj = L
    return aj

def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
    dataMatrix =np.mat(dataMatIn); labelMat = np.mat(classLabels).transpose()
    b = 0
    m,n = np.shape(dataMatrix)
    alphas = np.mat(np.zeros((m,1)))
    iter = 0
    while (iter < maxIter):
        alphaPairsChanged = 0
        for i in range(m):
            fXi = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
            Ei = fXi - float(labelMat[i])
            if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
                j = selectJrand(i,m)
                fXj = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
                Ej = fXj - float(labelMat[j])
                alphaIold = alphas[i].copy(); alphaJold = alphas[j].copy();
                if (labelMat[i] != labelMat[j]):
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if L==H:
                    continue
                eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
                if eta >= 0:
                    continue
                alphas[j] -= labelMat[j]*(Ei - Ej)/eta
                alphas[j] = clipAlpha(alphas[j],H,L)
                if (abs(alphas[j] - alphaJold) < 0.00001): 
                    continue
                alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])
                b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
                b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
                if (0 < alphas[i]) and (C > alphas[i]): b = b1
                elif (0 < alphas[j]) and (C > alphas[j]): b = b2
                else: b = (b1 + b2)/2.0
                alphaPairsChanged += 1
                print("iter: %d i:%d, pairs changed %d"%(iter,i,alphaPairsChanged))
        if (alphaPairsChanged == 0): iter += 1
        else: iter = 0
        print("iteration number: %d" % iter)
    print (alphas[alphas>0])
    return b,alphas
##w,b
def weight(alphas):
    m,n=np.shape(alphas)
    X_train,y_train=load_data()
    a,b=np.shape(X_train)##nan**2
    weights=np.zeros((b,1))
    for i in range(m):
        weights[0][0]+=alphas[i]*y_train[i]*X_train[0][i]
        weights[1][0]+=alphas[i]*y_train[i]*X_train[1][i]
    return weights
##plot
def plot(weights,b,alphas):
    bias=np.float(b)
    X_train,y_train=load_data()
    X_train=np.mat(X_train)
    y_train=np.mat(y_train).T
    m,n=np.shape(X_train)##2*3
    x_cord1=[];y_cord1=[]
    x_cord2=[];y_cord2=[]
    for i in range(n):
        if int(y_train[i]==1):
            x_cord1.append(X_train[0,i]);y_cord1.append(X_train[1,i])
        else:
            x_cord2.append(X_train[0,i]);y_cord2.append(X_train[1,i])
    fig=plt.figure()
    ax=fig.add_subplot(111)
    ax.scatter(x_cord1,y_cord1,s=30,c='r',marker='s')
    ax.scatter(x_cord2,y_cord2,s=30,c='g')
    x=np.arange(1,4,0.1)
    y=(-bias-weights[0][0]*x)/weights[1][0]
    ax.plot(x,y)
    plt.show()

dataMatIn, classLabels=load_data()
bias,alphas=smoSimple(dataMatIn.T, classLabels, 1000, 0.001, 40)
weights=weight(alphas)
plot(weights,bias,alphas)

bp算法：

    上面分析指出，对于单个感知机可以解决线性可分问题，但是对于线性不可分问题没有提出解决方案。在svm中，采用核技巧，可以解决线性不可分问题。bp算法的提出，使得利用神经网络解决线性不可分问题成为了可能。它的主要想法是：整体网络是向前传播的，而误差是向后传播的，所以我们可以利用梯度下降，从后往前调整权值。这里我们采用的误差函数依然是MSE（其实也可以采用交叉熵，从某种意义上讲，交叉熵在某些问题上比MSE更具有优越性），,由于其是从后向前传播的，所以利用随机梯度下降和链式法则，以及激活函数sigmoid的导数形式，我们可以求解出基于Loss最小化的个参数更新公式：（为隐层第h个神经元与输出层第j个神经元之间连线的更新公式），（为输出层第j个神经元的偏置更新公式），（为隐层第h个神经元与输入层第i个神经元之间的更新公式），（为隐层第h个神经元的偏置更新公式），下面给出xor利用bp算法的拟合程序。

import numpy as np
import matplotlib.pyplot as plt

##load
def load_data():
    X_train=np.array([[1,1,0,0],[1,0,1,0]]).T
    y_train=np.array([0,1,1,0]).reshape(-1,1)
    return X_train,y_train
##sigmoid
def sigmoid(x):
    return 1/(1+np.exp(-x))
##bp
def bp(X_train,y_train):
    m,n=np.shape(X_train)##4*2
    in_node=n;hide_node=6;out_node=1
    v=np.random.random((in_node,hide_node))##2*6
    w=np.random.random((hide_node,out_node))##6*1
    r=np.random.random((hide_node,1))##6*1
    theta=np.random.random()##1
    max_cnt=10000
    alpha=0.3
    for i in range(max_cnt):
        for j in range(m):
            hide_out=sigmoid(np.dot(X_train[j],v).T.reshape(-1,1)+r)##6*1
            predict=sigmoid(np.dot(hide_out.T,w)+theta)
            error=y_train[j]-predict
            g=predict*(1-predict)*error
            e=hide_out*(1-hide_out)*w*g##6*1
            w+=alpha*g*hide_out
            v+=alpha*np.dot(X_train[j].T.reshape(-1,1),e.T)
            theta+=alpha*g
            r+=alpha*e
    hide_out=sigmoid((np.dot(X_train,v).T)+r)##6*4
    predict=sigmoid(np.dot(hide_out.T,w)+theta)
    print(predict)
X_train,y_train=load_data()
bp(X_train,y_train)

EM算法（expectation maximizition）:

    上面的所有算法基于的思想都是训练集数据及标签已知，其中没有隐藏变量。然而现实中这种数据的来源十分有限，并且有的数据标签(例如生物学上的分类）需要耗费大量的人力物力才能实现，所以我们迫切需要一种算法来实现对于含有隐藏数据标签样本的估计。EM算法的主要思想是通过已知值建立一个模型，然后对未知值进行估计，最后进行迭代操作，直到模型与隐藏值都稳定，即是我们最后成熟的模型。EM算法推导的过程基于Jeson不等式，即若f是下凸函数，则。我们假设Z是隐藏变量，Y是已知变量，即（Y,Z）为完全数据，Y的似然函数是，全数据的似然函数是，这里我们采用的是极大似然估计参数（因为极大似然可以得到凸函数）。我们得到，我们的目标是求出这个式子的极大值。然而，由于其中含有隐变量Z，我们没有办法直接求出，所以我们寻找了一种新的方法，不断更新这个函数的下限，利用下限来逼近这个函数的最大值。，由于log函数为上凸函数，所以利用Jesson不等式，得出，在迭代的过程中，不断调整下限，可以得出该式的极大值。由Jesson不等式可知，当等式取等号时，，且，所以，所以，由此我们得出了隐变量的分布，在确定了隐变量之后，我们可以求解出极大值。具体的步骤：E步：根据第i次参数值，在i+1次中估计隐变量；M步：求使得第i次极大的参数值，确定第i+1次参数值。以下给出的是基于周志华老师《机器学习》中的西瓜数据集，利用EM进行高斯混合聚类的python实现。

#!/usr/bin/env python2
# -*- coding: utf-8 -*-
"""
Created on Fri Apr 13 14:20:29 2018

@author: luoyan
"""

import numpy as np
import matplotlib.pyplot as plt
##load
def load_data(filename):
    dataSet=[]
    fr=open(filename)
    for line in fr.readlines():
        curLine=line.strip().split('\t')
        fltLine=list(map(float,curLine))
        dataSet.append(fltLine)
    return dataSet
##Gauss
def Gauss(x,mu,sigma):
    n=np.shape(x)[1]
    eup=float((-1/2)*(x-mu)*(sigma.I)*((x-mu).T))
    div=pow(2*np.math.pi,n/2)*pow(np.linalg.det(sigma),0.5)
    return np.exp(eup)/div
##em
def EM(dataMat,maxIter=50):
    m,n=np.shape(dataMat)
    alpha=[0.3333,0.3333,0.3334]
    mu=[dataMat[5,:],dataMat[21,:],dataMat[26,:]]
    sigma=[np.mat([[0.1,0],[0,0.1]])for x in range(3)]
    gamma=np.mat(np.zeros((m,3)))
    for i in range(maxIter):
        for j in range(m):
            sumAlphaMulP=0
            for k in range(3):
                gamma[j,k]=alpha[k]*Gauss(dataMat[j,:],mu[k],sigma[k])
                sumAlphaMulP+=gamma[j,k]
            for k in range(3):
                gamma[j,k]/=sumAlphaMulP
        sumgamma=np.sum(gamma,axis=0)
        for k in  range(3):
            mu[k]=np.mat(np.zeros((1,n)))
            sigma[k]=np.mat(np.zeros((n,n)))
            for j in range(m):
                mu[k]+=gamma[j,k]*dataMat[j,:]
            mu[k]/=sumgamma[0,k]
            for j in range(m):
                sigma[k]+=gamma[j,k]*(dataMat[j,:]-mu[k]).T*(dataMat[j,:]-mu[k])
            sigma[k]/=sumgamma[0,k]
    return gamma
##Gausscluster
def gaussianCluster(dataMat):
    m,n=np.shape(dataMat)
    clusterAssign=np.mat(np.zeros((m,2)))
    gamma=EM(dataMat)
    for i in range(m):
        clusterAssign[i,:]=np.argmax(gamma[i,:]),np.amax(gamma[i,:])
    return clusterAssign
##plot
def plot(dataMat,clusterAssign):
    m,n=np.shape(dataMat)
    mark=['or','^b','sg','ok','^r','+r','sr','dr','

主成分分析（Principal Component Analysis）：

    PCA与LDA一样是一种降维方法，与LDA不同的是，PCA实现的降维是一种无监督学习下的降维，它基于的是最近重构性（样本点到这个超平面的距离都足够近）以及最大可分性（样本点在这个超平面的投影都尽可能地分开）。换一句说，我们希望在低维平面上的重构后的x与原始数据x距离最近，即，其中D的shape为n*l，，该最小化函数为，得到最后的优化目标为，，求解这个最小化问题就是对c求梯度，，，得出了低维向量。接下来我们可以利用这个向量最小化距离。，。求解这个最优化问题可以引入拉格朗日算子，并对d求梯度。

import numpy as np
import matplotlib.pyplot as plt
##load
def load_data(filename,delim='\t'):
    fr=open(filename)
    stringArr=[line.strip().split(delim)for line in fr.readlines()]
    datArr=[list(map(float,line))for line in stringArr]
    return np.mat(datArr)
##pca
def pca(dataMat,topNfeat=9999999):
    meanVals=np.mean(dataMat,axis=0)
    meanRemoved=dataMat-meanVals
    covMat=np.cov(meanRemoved,rowvar=0)
    eigVals,eigVects=np.linalg.eig(covMat)
    eigValInd=np.argsort(eigVals)
    eigValInd=eigValInd[:-(topNfeat+1):-1]
    theta=np.sum(eigVals[:-(topNfeat+1):-1])/np.sum(eigVals)
    redEigVects=eigVects[:,eigValInd]
    lowDDataMat=np.dot(meanRemoved,redEigVects)
    reconMat=np.dot(lowDDataMat,redEigVects.T)+meanVals
    return lowDDataMat,reconMat
##plot
def plot(dataMat,reconMat):
    fig=plt.figure()
    ax=fig.add_subplot(111)
    ax.scatter(dataMat[:,0].flatten().A[0],dataMat[:,1].flatten().A[0],marker='^',s=90)
    ax.scatter(reconMat[:,0].flatten().A[0],reconMat[:,1].flatten().A[0],marker='o',s=50,c='r')
    plt.show()
dataMat=load_data('testSet0.txt')
lowData,reconMat=pca(dataMat,1)
plot(dataMat,reconMat)