Professor Forcing: A New Algorithm for Training Recurrent Networks翻译
摘要
Teacher Forcing算法通过在训练的时候,将目标输出作为输入并使用网络自己的一次性预测来进行多步采样,从而对循环神经网络进行训练。我们引入Professor Forcing算法,在训练网络以及在多个时刻从网络采样时,使用对抗域自适应(adversarial domain adaptation)来鼓励循环网络的动态变化相同。我们将Professor Forcing应用到语言模型,原始波形的声音合成,笔迹生成和图像生成。经验上,我们发现Professor Forcing作为正则化,提高了字符级Penn Treebank以及顺序MNIST的测试概率。我们还发现该模型定性地改进了样本,特别是在对含有大量时间步骤的数据进行采样时。这是由人类对样品质量的评价所支持的。通过在Professor Forcing和Scheduled Sampling之间比较,我们提出T-SNEs展示出Professor Forcing成功地使训练和采样过程中的网络动态更加相似。
1.介绍
循环神经网络(RNNs)已经成为用于生成序列数据而选择的生成模型,它在语言模型,语音识别,机器翻译,笔迹生成,图像生成等应用中具有非常好的结果。
RNN通过一个全连通的有向图模型对数据建模:它将离散的时间序列 y 1 , y 2 , . . . , y T y_1,y_2,...,y_T y1,y2,...,yT分布分解为字符的条件概率分布:
P ( y 1 , y 2 , . . . , y T ) = P ( y 1 ) ∏ t = 1 T P ( y t ∣ y 1 , . . . , y t − 1 ) P(y_1,y_2,...,y_T)=P(y_1)\prod^T_{t=1}P(y_t|y_1,...,y_{t-1}) P(y1,y2,...,yT)=P(y1)t=1∏TP(yt∣y1,...,yt−1)
目前为止最受欢迎的训练策略是通过最大似然原则(maximum likelihood principle)。在与RNN有关的文献中,这种形式的训练方法也称为teacher forcing,由于使用了真值样本 y t y_t yt,因此将其反馈到模型中,以便对后一时刻输出进行预测。这种反馈迫使(force)RNN接近真实序列。
当使用RNN来进行预测时,真实样本序列是无效的条件,我们只能通过在给定先前生成的样本的条件分布中对每个 y t y_t yt进行采样来从序列上的联合分布中进行采样。不幸的是,在序列生成过程中,当一个小的预测错误发生时,这个过程会产生问题。当RNN的条件上下文(即先前生成的样本的序列)与训练时所使用的序列不一致时,这会导致一个非常差的性能。
最近,(Bengio et al., 2015)提出了通过在训练过程中混合两种类型输入来补救这个问题:一个输入是真实的训练序列,另外一个输入是从模型中产生的实际序列。然而,当模型连续生成几个 y t y_t yt后,正确的目标序列(就其分布而言)是否仍然是真实训练序列中的目标序列,这是不确定的。通过使自生成的子序列缩短并使用自生成序列对比真实样本序列的概率退火,可以通过各种方式减轻这种情况。然而,正如Huszár所说,scheduled sampling产生一个有偏估计,即使样本数和容量变为无穷大,此过程也可能无法收敛到正确的模型。然而,值得注意的是,scheduled sampling的实验清楚地显示了生成序列的健壮性方面的一些改进,表明确实需要通过生成RNN的最大似然(或teacher forcing)训练来修复(或替换)某些事物。
在这篇论文中,我们提出了一种训练RNNs的替代方法,该方法使生成行为和teacher-forced行为尽可能地匹配。这对于允许RNN继续产生远远超过其在训练期间看到的序列长度的特别重要。更一般地说,我们认为这种方法有助于通过使用训练对象来更好地建模长期依赖性,该对象不仅仅集中于一次一步地预测下一次观察。
我们的工作为这一新的训练框架提供了以下贡献:
- 我们引入了一种被称为Professor Forcing的新的训练RNNs的方法,其能成功的提高从循环网络中进行长时采样的能力。我们通过与人类评估员一起进行研究,通过人类评估样本质量来证明这一点。
- 我们发现Professor Forcing能够作为循环网络的一个正则化项。这通过在字符级Penn Treebank,序列MNIST生成和语音合成上进行测试概率的提高来证明。有趣的是,我们还发现训练效率也可以被提高,我们猜测这是因为可以更容易地捕获长期依赖关系。
- 在采样模式下运行RNN时,网络隐藏状态占用的区域与teacher forcing时占用的区域不同。 我们使用T-SNE凭经验研究这一现象,并表明可以通过使用Professor Forcing来减轻这种现象。
- 在一些领域中,训练时可用的序列比我们想要在测试时生成的序列短。这通常是长期预测任务(气候建模,计量经济学)的情况。我们将展示如何使用Professor Forcing来提高此设置的性能。请注意,scheduled sampling不能用于此任务,因为它仍然使用观察到的序列作为网络的目标。
2.提出的方法:Professor Forcing
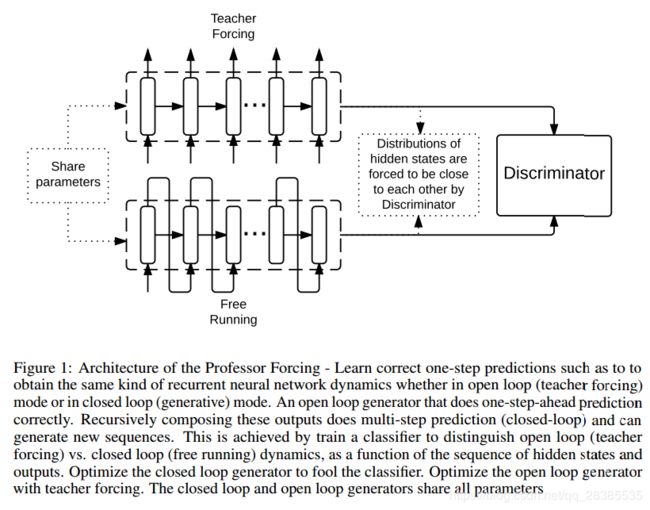
Professor Forcing的基本观点很简单:虽然我们确实希望生成RNN与训练数据相匹配,但我们还希望网络的行为(无论是在其输出中还是在其隐藏状态的动态中)能无法区分网络是否受到训练且其输入被限制在训练序列中(teacher forcing模式)或其输入是否是自生成的(自由运行的生成模式)。由于我们仅能够比较这些序列的分布,利用生成对抗网络(GANs)框架(Goodfellow et al., 2014)来实现第二个目标,即将两个序列分布相匹配(在teacher forcing模式中观察到的序列与在自由模式中观察到的序列)是有意义的。
因此,除了生产RNN以外,我们还会训练第二个模型,这个模型我们称为判别器,其同样能够处理可变长度的输入。在实验中,对于判别器来说,我们使用双向RNN结构,因而其能够将每一时刻 t t t的过去行为序列和未来行为序列联合起来进行判别。
2.1 定义和符号
(1)令训练分布提供输入和输出序列 ( x , y ) (x,y) (x,y)对(可能根本没有输入)。根据Seq2Seq模型分布 P θ g ( y ∣ x ) P_{\theta_{g}}(y|x) Pθg(y∣x),当给定一个输入序列 x x x,输出序列 y y y能够由生成器RNN生成。
(2)令 θ g \theta_{g} θg作为生成RNN的参数, θ d \theta_{d} θd作为判别器的参数。
(3)判别器被训练为概率分类器,当生成或受到序列 y y y的约束时,可以在输入序列 x x x的上下文(不必与 y y y的长度相同)中将来自于生成RNN的(隐藏和输出)活动的行为序列 b b b作为输入。行为序列 b b b要么来自于在teacher forcing模式下生成RNN的运行结果(来自具有输入 x x x的训练序列中的 y y y),要么来自于free-running模式下的运行结果(根据 P θ g ( y ∣ x ) P_{\theta_{g}}(y|x) Pθg(y∣x)自生成 y y y, 与训练序列中的 x x x)。
(4)给定适当数据(其中x总是来自训练数据,但是y来自训练数据或是自生成的)的函数 B ( x , y , θ g ) B(x,y,θ_g) B(x,y,θg)输出行为序列(选择的隐藏状态和输出值)。
(5)设 D ( b ) D(b) D(b)为判别器的输出,估计在teacher forcing模式下产生 b b b的概率,假设判别器看到的一半例子是在teacher forcing模式下产生的,一半是在free-running模式中产生的。
注意,在生成器RNN没有任何条件输入的情况下,序列 x x x是空的。还要注意,生成的输出序列可以具有与输入序列不同的长度,这取决于所处理的任务。
2.2 训练目标
(1)判别器训练
判别器参数 θ d θ_d θd按照预期进行训练,例如,最大化正确分类行为序列的概率:
C d ( θ d ∣ θ g ) = E ( x , y ) ∼ d a t a [ − l o g D ( B ( x , y , θ g ) , θ d ) + E y ∼ P θ g ( y ∣ x ) [ − l o g 1 − D ( B ( x , y , θ g ) , θ d ) ] ] ( 1 ) C_d(\theta_d|\theta_g)=E_{(x,y)\sim data}[-logD(B(x,y,\theta_g),\theta_d)+E_{y\sim P_{\theta_g(y|x)}}[-log1-D(B(x,y,\theta_g),\theta_d)]]\qquad(1) Cd(θd∣θg)=E(x,y)∼data[−logD(B(x,y,θg),θd)+Ey∼Pθg(y∣x)[−log1−D(B(x,y,θg),θd)]](1)
特别地,通过联合以teacher-forcing模式生成的N个序列,以free-running模式,从 P θ g ( y ∣ x ) P_{\theta_g}(y|x) Pθg(y∣x)采样 y y y的N个序列,采用mini-batches形式的随机梯度下降来实现。还要注意,当 θ g θ_g θg改变时,由判别器优化的任务也改变,并且它必须跟踪生成器,如在其他GAN设置中那样,因此标记 C d ( θ d ∣ θ g ) C_d(θ_d|θ_g) Cd(θd∣θg)。
(2)生成器训练
生成器RNN的参数 θ g \theta_g θg按(a)最大化数据概率(b)愚弄判别器这两种方式进行训练。我们考虑了后者的两种变体。 负对数似然目标(a)是RNN通常的teacher forcing训练标准:
N L L ( θ g ) = E ( x , y ) ∼ d a t a [ − l o g P θ g ( y ∣ x ) ] ( 2 ) NLL(\theta_g)=E_{(x,y)\sim data}[-logP_{\theta_g}(y|x)]\qquad(2) NLL(θg)=E(x,y)∼data[−logPθg(y∣x)](2)
关于(b)我们考虑的训练目标只是试图改变free-running行为,以便更好地匹配teacher forcing行为,考虑到后者已修复:
C f ( θ g ∣ θ d ) = E x ∼ d a t a , y ∼ P θ g ( y ∣ x ) [ − l o g D ( B ( x , y , θ g ) , θ d ) ] ( 3 ) C_f(\theta_g|\theta_d)=E_{x\sim data,y\sim P_{\theta_g}(y|x)}[-logD(B(x,y,\theta_g),\theta_d)]\qquad(3) Cf(θg∣θd)=Ex∼data,y∼Pθg(y∣x)[−logD(B(x,y,θg),θd)](3)
另外(可选地),我们可以要求teacher forcing行为与free-running行为无法区分:
C t ( θ g ∣ θ d ) = E ( x , y ) ∼ d a t a [ − l o g ( 1 − D ( B ( x , y , θ g ) , θ d ) ) ] ( 4 ) C_t(\theta_g|\theta_d)=E_{(x,y)\sim data}[-log(1-D(B(x,y,\theta_g),\theta_d))]\qquad(4) Ct(θg∣θd)=E(x,y)∼data[−log(1−D(B(x,y,θg),θd))](4)
在我们的实验中,我们要么在 N L L + C f NLL+C_f NLL+Cf或 N L L + C f + C t NLL+C_f+C_t NLL+Cf+Ct上执行随机梯度步骤,从而更新生成RNN的参数,而我们总是在 C d C_d Cd上执行梯度步骤以更新判别器的参数。
3.相关工作
4.实验
4.1 网络结构和Professor Forcing设置
(1)生成器
在实验中所使用的神经网络和Professor Forcing设置如下。生成RNN使用门循环单元(GRU)的单独隐藏层,其作为LSTM单元的一个更简化的版本。
(a)在每一时刻,生成RNN读取输入序列(如果有)的一个元素 x t x_t xt,以及输出序列 y y y的一个元素 y t y_t yt(该元素要么来自训练数据,要么来自RNN上一时刻的输出)。
(b)然后以上一状态 h t − 1 h_{t-1} ht−1和当前输入 ( x t , y t ) (x_t,y_t) (xt,yt)构成的函数更新状态 h t h_t ht。
(c)然后计算下一个输入元素的概率分布 P θ g ( y t + 1 ∣ h t ) = P θ g ( y t + 1 ∣ x 1 , . . . , x t , y 1 , . . . , y t ) P_{\theta_g}(y_{t+1}|h_t)=P_{\theta_g}(y_{t+1}|x_1,...,x_t,y_1,...,y_t) Pθg(yt+1∣ht)=Pθg(yt+1∣x1,...,xt,y1,...,yt)。对于离散输出,可以在 h t h_t ht上增加一个Softmax/attine层实现,其输出数目等于 y t y_t yt能够取得的值的数目。在free-running模式, y t + 1 y_{t+1} yt+1从分布中采用,并作为下一时刻的输入。或者,用真值 y t y_t yt作为输入。
在实验中使用的行为函数 B B B输出所考虑的整个序列GRU状态的tanh激活值,并且对于整个序列,可选地输出用于下一步预测的softmax输出。
(2)判别器