数据结构与算法 -- 栈 ADT
这两天翻了下数据结构与算法分析、严蔚敏的数据结构、C和指针、C Primer Plus这些本书,受益很多。不过大多的示例不够完整,需要自己动手编写程序。又看了遍培训时的笔记,虽然很糙但是精华的部分还是可以借鉴的。还有看到了不错的博文,参看:数据结构与算法分析 学习笔记 对于数据结构与算法,尽量做到多方面的参考。多的不说了,下面就开始总结!!
一、首先讲一些基本的概念
1、数据结构的基本概念
在计算机学科中数据结构表示数据在计算机中的存储和组织形式。主要描述数据元素之间和位置关系等。一般来说,选择适当的数据结构可以提高计算机程序的运行效率(时间复杂度)和存储效率(空间复杂度)。
2、数据结构的三种层次
(1)逻辑结构--抽象层
主要描述的是数据元素之间的逻辑关系
(2)物理结构--结构层
主要描述的是数据元素之间的位置关系
(3)运算结构--实现层
主要描述的是如何实现数据结构
3、逻辑结构的分类 (抽象数据类型 ADT)
(1)集合结构(集)
主要描述所有的元素都属于一个总体,除了同属于一个集合外没有其他关系。集合结构不强调元素之间的任何关联性。
(2)线性结构(表)
主要描述元素之间具有一对一的前后关系。结构中必须存在唯一的首元素和唯一的尾元素。除了首元素之外结构中的每一个元素有且仅有一个前趋元素,除了尾元素之外结构中的每一个元素有且仅有一个后继元素。
(3)树形结构(树)
主要描述元素之间存在一对一个关系。树形结构中必须存在唯一跟关系,顶端的元素叫做叶元素。除了根元素之外,结构中每一个元素有且仅有一个前趋元素,除了叶元素之外,结构中每一个元素拥有一个到多个后继元素。如:树,家谱。
(4)网状结构(图)
主要描述数据元素之间存在多对多的交叉映射关系,也叫做图形结构。结构中的每个元素都可以拥有多个任意数量,前驱和后继元素,结构中的任意两个元素都可以建立关联。如:蜘蛛网 网球拍。
4、物理结构的分类
(1)顺序结构
顺序结构就是使用一组连续的存储单元依次存储逻辑上相邻的各个元素,顺序结构可以借助计算机程序设计语言(如C/C++)提供的数组类型加以描述。
优点:
只需要申请存放数据本身的内存空间即可,不需要额外的内存来表达数据元素之间的逻辑关系。
支持下标访问,也可以实现随机访问。
缺点:
连续的存储空间导致内存空间的利用率比较低。
向顺序存储结构中插入/删除元素时,可能需要移动大量元素,效率比较低。
(2)链式结构
表示在计算机中使用一组任意的存储单元来存储所有的元素(这组存储单元可以是连续的,也可以是不连续的)。不要求逻辑上相邻的元素在物理位置上也相邻。
链式存储结构不使用连续的存储空间存放结构的元素,而是为每一个元素构造一个节点。节点中除了存放数据本身以外,还需要存放指向下一个节点的指针。绝大多数程序设计语言(如C/C++)都没有提供用于描述链式结构的数据类型,需要编写额外的代码去实现。
优点:
不采用连续的存储空间导致内存空间利用率比较高,克服顺序存储结构中预知元素个数的缺点
插入或删除元素时,不需要移动大量的元素,比较当便。
缺点:
除了申请存放数据本身的内存空间外,还需要额外的空间来表达数据之间的逻辑关系
不支持下标访问和随机访问。
5、逻辑结构和物理结构的关系
每种逻辑结构采用何种物理结构来实现,并没有具体的规定。通过根据实现的难易程度,以及在时间复杂程度和空间复杂程度方面的要求,来选择合适的物理结构。
6、运算结构
(1)分配资源,建立结构,释放资源
如:int arr[5]; ->栈区,系统自动分配内存和回收内存。
(2)插入和删除
增加和减少元素
(3)获取和遍历
查看具体的元素值,以及遍历结构中所有的元素值
(4)修改和排序
修改元素的值,采用排序算法进行排序
二、栈 ADT
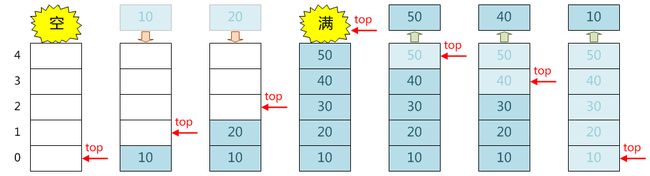
三、顺序栈
静态数组:特点是要求结构的长度固定,而且长度在编译时候就得确定。其优点是结构简单,实现起来方便而不容易出错。而缺点就是不够灵活以及固定长度不容易控制,适用于知道明确长度的场合。
动态数组:特点是长度可以在运行时候才确定以及可以更改原来数组的长度。优点是灵活,缺点是由此会增加程序的复杂性。
1、静态数组
travel ();
pop ();
输出结果:
这个栈为空
栈为空
a.out: a_stack.c:73: pop: Assertion `!is_empty ()' failed.
已放弃 (核心已转储)#include
#include
#include
#define STACK_TYPE int /* 堆栈所存储的值的数据类型 */
#define STACK_SIZE 100 /* 堆栈最大容纳元素数量 */
/* 存储堆栈中的数组和一个指向堆栈顶部元素的指针 */
static STACK_TYPE stack[STACK_SIZE];
static int top_element = -1;
/* 将一个新值压入堆栈中,参数是被压入的值。*/
void push (STACK_TYPE value);
/* 弹出堆栈中栈顶的一个值,并丢弃。*/
void pop (void);
/* 返回堆栈顶部元素的值,但不改变堆栈结构。*/
STACK_TYPE top (void);
/* 如果堆栈为空,返回TRUE,否则返回FALSE。*/
int is_empty (void);
/* 如果堆栈为满,返回TRUE,否则返回FALSE。*/
int is_full (void);
/* 自定义函数实现遍历操作 */
void travel (void);
/* 计算栈中元素的个数 */
int size (void);
int main (void)
{
travel ();
pop ();
printf("%s\n", is_empty() ? "栈为空" : "栈未空");
int i = 0;
for (i = 0; i <= 9; i++)
{
push (i);
}
puts ("push 压栈后的数值为: ");
travel ();
printf ("此时栈顶元素为:%d\n", top ());
printf ("此时栈元素个数为:%d\n", size ());
pop ();
pop ();
puts ("经过pop弹出几个元素后的栈元素: ");
travel ();
printf("%s\n", is_full() ? "栈为满" : "栈未满");
printf("%s\n", is_empty() ? "栈为空" : "栈未空");
printf ("此时栈顶元素为:%d\n", top ());
printf ("此时栈元素个数为:%d\n", size ());
return 0;
}
void push (STACK_TYPE value)
{
//assert (!is_full ()); /* 压入堆栈之前先判断是否堆栈已满*/
if (is_full ())
{
printf ("栈已满,入栈失败\n");
return ;
}
top_element += 1;
stack[top_element] = value;
}
void pop (void)
{
//assert (!is_empty ()); /* 弹出堆栈之前先判断是否堆栈已空 */
if (is_empty ())
{
printf ("栈已空,出栈失败\n");
return ;
}
top_element -= 1;
}
STACK_TYPE top (void)
{
//assert (!is_empty ());
if (is_empty ())
{
printf ("栈已空,出栈失败\n");
return ;
}
return stack[top_element];
}
int is_empty (void)
{
return top_element == -1;
}
int is_full (void)
{
return top_element == STACK_SIZE -1;
}
void travel (void)
{
int i = 0;
if (top_element == -1)
printf ("这个栈为空");
for (i = 0; i <= top_element; i++)
printf ("%d ", stack[i]);
printf ("\n");
}
int size (void)
{
return top_element + 1;
}
输出结果:
这个栈为空
栈已空,出栈失败
栈为空
push 压栈后的数值为:
0 1 2 3 4 5 6 7 8 9
此时栈顶元素为:9
此时栈元素个数为:10
经过pop弹出几个元素后的栈元素:
0 1 2 3 4 5 6 7
栈未满
栈未空
此时栈顶元素为:7
此时栈元素个数为:8 2、动态数组
/* 堆栈的长度在创建堆栈的函数被调用时给出,该函数必须在任何其他操作堆栈的函数被调用之前调用 */
#include
#include
#include
#define STACK_TYPE int /* 堆栈所存储的值的数据类型 */
/* 用于存储堆栈元素的数组和指向堆栈顶部元素的指针 */
static STACK_TYPE *stack;
static int stack_size;
static int top_element = -1;
/*
创建对栈,参数指定对栈可以保存多少个元素
注意:此函数只适用于动态分配数组形式的堆栈。
*/
void create_stack (size_t size);
/*
销毁一个堆栈,释放堆栈所适用的内存
注意,此函数只适用于动态分配数组和链表结构的堆栈。
*/
void destroy_stack (void);
/* 将一个新值压入堆栈中,参数是被压入的值。*/
void push (STACK_TYPE value);
/* 弹出堆栈中栈顶的一个值,并丢弃。*/
void pop (void);
/* 返回堆栈顶部元素的值,但不改变堆栈结构。*/
STACK_TYPE top (void);
/* 如果堆栈为空,返回TRUE,否则返回FALSE。*/
int is_empty (void);
/* 如果堆栈为满,返回TRUE,否则返回FALSE。*/
int is_full (void);
/* 自定义函数实现遍历操作 */
void travel (void);
/* 计算栈中元素的个数 */
int size (void);
int main (void)
{
create_stack (50);
travel ();
pop ();
printf("%s\n", is_empty() ? "栈为空" : "栈未空");
int i = 0;
for (i = 0; i <= 9; i++)
{
push (i);
}
puts ("push 压栈后的数值为: ");
travel ();
printf ("此时栈顶元素为:%d\n", top ());
printf ("此时栈元素个数为:%d\n", size ());
pop ();
pop ();
puts ("经过pop弹出几个元素后的栈元素: ");
travel ();
printf("%s\n", is_full() ? "栈为满" : "栈未满");
printf("%s\n", is_empty() ? "栈为空" : "栈未空");
printf ("此时栈顶元素为:%d\n", top ());
printf ("此时栈元素个数为:%d\n", size ());
destroy_stack ();
printf ("此时栈元素个数为:%d\n", size ());
return 0;
}
void create_stack (size_t size)
{
//assert (stack_size == 0);
if (size < stack_size)
{
printf ("栈元素个数太少\n");
return ;
}
stack_size = size;
stack = (STACK_TYPE *)malloc (stack_size * sizeof (STACK_TYPE));
if (NULL == stack)
perror ("malloc分配失败"), exit (1);
}
void destroy_stack (void)
{
//assert (stack_size > 0);
if (stack != NULL)
{
printf ("销毁堆栈\n");
stack_size = 0;
free (stack);
stack = NULL;
top_element = -1;
}
}
void push (STACK_TYPE value)
{
//assert (!is_full ());
if (is_full ())
{
printf ("栈已满,入栈失败\n");
return ;
}
top_element += 1;
stack[top_element] = value;
}
void pop (void)
{
//assert (!is_empty ());
if (is_empty ())
{
printf ("栈已空,出栈失败\n");
return ;
}
top_element -= 1;
}
STACK_TYPE top (void)
{
//assert (!is_empty ());
if (is_empty ())
{
printf ("栈已空,出栈失败\n");
return ;
}
return stack[top_element];
}
int is_empty (void)
{
//assert (stack_size > 0);
if (stack != NULL)
{
return top_element == -1;
}
}
int is_full (void)
{
//assert (stack_size > 0);
if (stack != NULL)
{
return top_element == stack_size - 1;
}
}
void travel (void)
{
int i = 0;
if (top_element == -1)
printf ("这个栈为空");
for (i = 0; i <= top_element; i++)
printf ("%d ", stack[i]);
printf ("\n");
}
int size (void)
{
return top_element + 1;
}
输出结果:
这个栈为空
栈已空,出栈失败
栈为空
push 压栈后的数值为:
0 1 2 3 4 5 6 7 8 9
此时栈顶元素为:9
此时栈元素个数为:10
经过pop弹出几个元素后的栈元素:
0 1 2 3 4 5 6 7
栈未满
栈未空
此时栈顶元素为:7
此时栈元素个数为:8
销毁堆栈
此时栈元素个数为:0 3、自写顺序栈
//使用顺序存储结构实现栈的基本操作
#include
#include
#define SIZE 5
//给数据类型起别名,支持其他的数据类型
int arr[SIZE]; //存储具体的元素值
int pos; //记录数据的下表
//自定义函数实现入栈操作 //入栈==赋值
void push (int data);
//自定义函数实现遍历操作 // 遍历==打印
void travel (void);
//自定义函数实现出栈操作
int pop (void);
//查看栈顶元素
int top (void);
//判断栈是否为满
int full (void);
//判断栈是否为空
int empty (void);
//计算栈中元素的个数
int size (void);
int main (void)
{
printf ("出栈的元素是:%d\n", pop ());
printf ("栈顶元素是:%d\n", top ());
int i = 0;
for (i = 0; i <= 6; i++)
push (i);
travel ();
printf ("出栈的元素是:%d\n", pop ());
travel ();
printf ("栈顶元素是:%d\n", top ());
printf ("%s\n", full () ? "栈为满" : "栈未满");
printf ("%s\n", empty () ? "栈为空" : "栈未空");
printf ("栈元素个数为:%d\n", size ());
return 0;
}
void push (int data)
{
//判断为不为满 ,避免可能编译报错
if (full ())
{
printf ("栈已满,入栈失败\n");
return ;
}
arr[pos++] = data;
}
void travel (void)
{
printf ("栈中元素有:");
int i = 0;
for (i = 0; i <= pos - 1; i++)
printf ("%d ", arr[i]);
printf ("\n");
}
int pop (void)
{
//判断栈是否为空
if (!pos)
{
printf ("栈已空,出栈失败\n");
return ;
}
return arr[--pos];
}
int top (void)
{
//判断栈是否为空
if (!pos)
{
printf ("栈已空, 查看栈元素失败\n");
return ;
}
return arr[pos - 1];
}
int full (void)
{
return SIZE == pos;
}
int empty (void)
{
return 0 == pos;
}
int size (void)
{
return pos;
}
输出结果:
栈已空,出栈失败
出栈的元素是:25
栈已空, 查看栈元素失败
栈顶元素是:35
栈已满,入栈失败
栈已满,入栈失败
栈中元素有:0 1 2 3 4
出栈的元素是:4
栈中元素有:0 1 2 3
栈顶元素是:3
栈未满
栈未空
栈元素个数为:4 4、顺序栈总结
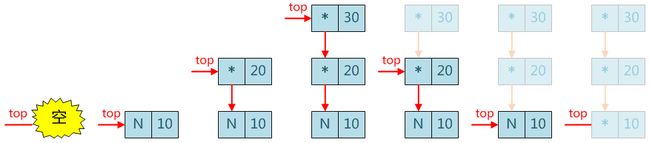
四、链式栈
1、链式栈
/* 单链表实现堆栈,没有长度限制 */
#include
#include
#include
#define STACK_TYPE int /* 堆栈所存储的值的数据类型 */
#define FALSE 0
/* 定义一个结构以存储堆栈元素。 */
typedef struct STACK_NODE
{
STACK_TYPE value;
struct STACK_NODE *next;
}StackNode;
/* 指向堆栈中第一个节点的指针 */
static StackNode *stack;
/*栈元素个数*/
static int cnt;
/*
创建对栈,参数指定对栈可以保存多少个元素
注意:此函数只适用于动态分配数组形式的堆栈。
*/
void create_stack (size_t size);
/*
销毁一个堆栈,释放堆栈所适用的内存
注意,此函数只适用于动态分配数组和链表结构的堆栈。
*/
void destroy_stack (void);
/* 将一个新值压入堆栈中,参数是被压入的值。*/
void push (STACK_TYPE value);
/* 弹出堆栈中栈顶的一个值,并丢弃。*/
void pop (void);
/* 返回堆栈顶部元素的值,但不改变堆栈结构。*/
STACK_TYPE top (void);
/* 如果堆栈为空,返回TRUE,否则返回FALSE。*/
int is_empty (void);
/* 如果堆栈为满,返回TRUE,否则返回FALSE。*/
int is_full (void);
/* 自定义函数实现遍历操作 */
void travel (void);
/* 计算栈中元素的个数 */
int size (void);
int main (void)
{
travel ();
pop ();
printf("%s\n", is_empty() ? "栈为空" : "栈未空");
int i = 0;
for (i = 0; i <= 9; i++)
{
push (i);
}
puts ("push 压栈后的数值为: ");
travel ();
printf ("此时栈顶元素为:%d\n", top ());
printf ("此时栈元素个数为:%d\n", size ());
pop ();
pop ();
puts ("经过pop弹出几个元素后的栈元素: ");
travel ();
printf("%s\n", is_full() ? "栈为满" : "栈未满");
printf("%s\n", is_empty() ? "栈为空" : "栈未空");
printf ("此时栈顶元素为:%d\n", top ());
printf ("此时栈元素个数为:%d\n", size ());
destroy_stack ();
printf ("此时栈元素个数为:%d\n", size ());
return 0;
}
/* 不再需要create_stack 函数 */
void create_stack (size_t size)
{}
void destroy_stack (void)
{
printf ("销毁堆栈\n");
while (!is_empty ())
pop (); /* 逐个弹出元素,逐个释放节点内存 */
}
void push (STACK_TYPE value)
{
StackNode *new_node;
new_node = (StackNode *)malloc (sizeof (StackNode));
if (NULL == new_node)
perror ("malloc fail");
new_node->value = value;
new_node->next = stack; /* 新元素插入链表头部 */
stack = new_node; /* stack 重新指向链表头部 */
cnt++;
}
void pop (void)
{
StackNode *first_node;
//assert (!is_empty ());
if (is_empty ())
{
printf ("栈已空,出栈失败\n");
return ;
}
first_node = stack;
stack = first_node->next;
free (first_node);
first_node = NULL;
cnt--;
}
STACK_TYPE top (void)
{
//assert (!is_empty ());
if (is_empty ())
{
printf ("栈已空,出栈失败\n");
return ;
}
return stack->value;
}
int is_empty (void)
{
return stack == NULL;
}
int is_full (void)
{
return FALSE;
}
void travel (void)
{
StackNode *p_node;
p_node = stack;
printf ("打印出链式堆栈里面的值:");
if (NULL == p_node)
printf ("堆栈为空\n");
while (p_node != NULL)
{
printf ("%d ", p_node->value);
p_node = p_node->next;
}
printf ("\n");
}
int size (void)
{
return cnt;
}
输出结果:
打印出链式堆栈里面的值:堆栈为空
栈已空,出栈失败
栈为空
push 压栈后的数值为:
打印出链式堆栈里面的值:9 8 7 6 5 4 3 2 1 0
此时栈顶元素为:9
此时栈元素个数为:10
经过pop弹出几个元素后的栈元素:
打印出链式堆栈里面的值:7 6 5 4 3 2 1 0
栈未满
栈未空
此时栈顶元素为:7
此时栈元素个数为:8
销毁堆栈
此时栈元素个数为:0 2、自写链式栈
//基于链式存储结构的堆栈实现
#include
#include
typedef struct Node
{
int data; //存放的具体元素
struct Node *next; //存放下一个节点地址
}Node;
typedef struct
{
int cnt;
Node *head;
}Stack;
//入栈操作
void push (Stack *ps, int data);
//遍历操作
void travel (Stack *ps);
//出栈操作
int pop (Stack *ps);
//查看栈顶元素
int top (Stack *ps);
//判断堆栈是否为空
int empty (Stack *ps);
//判断堆栈是否为满
int full (Stack *ps);
//查看堆栈元素个数
int size (Stack *ps);
int main (void)
{
Stack stack;
stack.head = 0;
stack.cnt = 0;
printf ("%s\n", empty (&stack)? "堆栈为空" : "堆栈未空");
printf ("出栈元素是:%d\n", pop (&stack));
printf ("堆栈中元素的个数为:%d\n", size (&stack));
printf ("--------------------------\n");
push (&stack, 11); //11
push (&stack, 22); //22 11
push (&stack, 33); //33 22 11
push (&stack, 44); //44 33 22 11
travel (&stack); //44 33 22 11
printf ("出栈元素是:%d\n", pop (&stack));
travel (&stack); //33 22 11
printf ("--------------------------\n");
printf ("栈顶元素为:%d\n", top (&stack));
printf ("%s\n", full (&stack) ? "堆栈为满" : "堆栈未满");
printf ("%s\n", empty (&stack)? "堆栈为空" : "堆栈未空");
printf ("堆栈中元素的个数为:%d\n", size (&stack));
return 0;
}
void push (Stack *ps, int data)
{
//创建新节点并初始化
Node *pn = (Node *)malloc (sizeof (Node));
pn->data = data;
pn->next = NULL;
//插入新节点
pn->next = ps->head;
ps->head = pn;
ps->cnt++;
}
void travel (Stack *ps)
{
printf ("堆栈中的元素有:\n");
Node *p = ps->head;
//判断堆栈为不为空
while (p != NULL)
{
printf ("%d ", p->data);
//指向下一个节点
p = p->next;
}
printf ("\n");
}
int pop (Stack *ps)
{
//判断为不为空
if (NULL == ps->head)
return ;
//保存要删除的节点地址
Node *p = ps->head;
//头指针指向下一个节点
ps->head = ps->head->next;
ps->cnt--;
//存储要删除的节点元素值
int tmp = p->data; //释放内存完毕后就没有元素值了
free (p); //释放内存
p = NULL; //置为空指针
return tmp;
}
int top (Stack *ps)
{
//判断堆栈是否为空
if (empty (ps))
return ;
return ps->head->data;
}
int empty (Stack *ps)
{
return NULL == ps->head;
}
int full (Stack *ps)
{
return 0;
}
int size (Stack *ps)
{
return ps->cnt;
}
输出结果:
堆栈为空
出栈元素是:0
堆栈中元素的个数为:0
--------------------------
堆栈中的元素有:
44 33 22 11
出栈元素是:44
堆栈中的元素有:
33 22 11
--------------------------
栈顶元素为:33
堆栈未满
堆栈未空
堆栈中元素的个数为:3 3、链式栈总结
五、栈实现计算器
2、当遇到运算符时,如果它的优先级比运算符栈栈顶元素的优先级高就进栈。反之,取出栈顶运算符和操作数栈顶
#include
#include
#define MAX_SIZE 1024
int operand[MAX_SIZE];
int top_num = -1;
char oper[MAX_SIZE];
int top_oper = -1;
//输入数据,将数据压入数据栈
void insert_operand (int value)
{
if (top_num == MAX_SIZE - 1)
return ;
top_num += 1;
operand[top_num] = value;
}
//输入操作符,将操作符压入符号栈
void insert_oper (char ch)
{
if (top_oper == MAX_SIZE - 1)
return ;
top_oper += 1;
oper[top_oper] = ch;
}
//比较操作符优先级
int compare (char ch)
{
//判断当前优先级是否比栈顶操作符优先级高
if ((oper[top_oper] == '-' || oper[top_oper] == '+') && (ch == '*' || ch == '/'))
return 0;
//判断操作符是否为空,栈顶操作符是否为'('
else if (top_oper == -1 || ch == '(' || (oper[top_oper] == '(' && ch != ')'))
return 0;
//判断括号内的表达式是否计算完毕
else if (oper[top_oper] == '(' && ch == ')')
{
top_oper--;
return 1;
}
else
return -1;
}
//进行数据运算
void deal_date (void)
{
//取出数据栈中两个数据
int num1 = operand[top_num];
int num2 = operand[top_num - 1];
int value = 0;
//进行加减乘除操作
if (oper[top_oper] == '+')
value = num1 + num2;
else if (oper[top_oper] == '-')
value = num2 -num1;
else if (oper[top_oper] == '*')
value = num1 * num2;
else if (oper[top_oper] == '/')
value = num2 / num1;
//将数据栈顶下移一位,然后将得到的值压入数据栈,将操作符栈顶下移一位
top_num--;
operand[top_num] = value;
top_oper--;
}
int main (void)
{
char ch;
int i = 0;
int num = 0;
char *temp;
char dest[MAX_SIZE];
char *str = (char*)malloc (sizeof (char) * MAX_SIZE);
scanf ("%s", str);
while (*str != '\0')
{
temp = dest;
while (*str >= '0' && *str <= '9') //判断是否为数据,遇到符号退出
*(temp++) = *(str++);
if (*str != '(' && *(temp - 1) != '\0') //判断是否为符号'('
{
*temp = '\0';
num = atoi (dest); //将字符串转为数字
insert_operand (num);
}
while (1)
{
i = compare (*str); //判断操作符优先级
if (i == 0) //压入操作符
{
insert_oper (*str);
break;
}
else if (i == 1) //判断括号内表达式是否结束
str++;
else if (i == -1) //进行数据处理
deal_date ();
}
str++; //指向表达式下一个字符
}
printf ("num = %d\n", operand[0]);
return 0;
}
输出结果:
1+2*(1+2)-2+(6/2)
num = 8 六、逆波兰式计算器
扩展:波兰式、逆波兰式与表达式求值
3/5+6的逆波兰表达式为3 5 / 6 +
2*(3+4)的逆波兰表达式为2 3 4 + *
#include
#include
int tranfer(char *s)
{
int k=1,result=0,len = strlen(s);
while(len--)
{
result += (s[len]-'0')*k;
k *= 10;
}
return result;
}
main( )
{
char s[50];
int j=0,num[100];
while((scanf("%s",s))!=EOF)
{
if(s[0]>='0'&&s[0]<='9')
num[j++] = tranfer(s);
else
{
switch(s[0]){
case '+':
num[j-2] += num[j-1];
j--;
break;
case '-':
num[j-2] -= num[j-1];
j--;
break;
case '*':
num[j-2] *= num[j-1];
j--;
break;
case '/':
num[j-2] /= num[j-1];
j--;
break;
}
}
}
printf("%d\n",num[0]);
}
输出结果:
2 3 + 5 *
(按 CTRL + D 结束)
num = 25