Pool层及其公式推导

在CNN网络中卷积池之后会跟上一个池化层，池化层的作用是提取局部均值与最大值，根据计算出来的值不一样就分为均值池化层与最大值池化层，一般常见的多为最大值池化层

设 al−1=σ(zl−1) a l − 1 = σ ( z l − 1 )

前向传播

maxpool

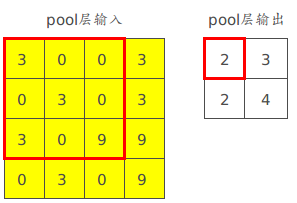
前向传播会记录每次pool的核移动stride后所在区域里的最大值,和最大值所在坐标
这里以pool的核的大小为3x3,stride=1为例,则pool后的值的输出和最大值所在坐标如下图:
设pool层输出为 al a l

alij=max(al−1mn),i≤m,n≤i+2其中m,n为al−1ij对应的pool核覆盖的区域,如下左图a00对应区域为红框所标记的区域 a i j l = m a x ( a m n l − 1 ) , i ≤ m , n ≤ i + 2 其 中 m , n 为 a i j l − 1 对 应 的 p o o l 核 覆 盖 的 区 域 , 如 下 左 图 a 00 对 应 区 域 为 红 框 所 标 记 的 区 域

avg pool

这里pool核的大小为3x3,stride=1

反向传播

maxpool

由于pool层没有参数,所以没必要求梯度,主要将相关的梯度传下即可:

δl−1k,v=∂C∂zl−1k,v=∑iji=3,j=3∂C∂alij∂alij∂al−1k,val−1k,v∂zl−1k,v δ k , v l − 1 = ∂ C ∂ z k , v l − 1 = ∑ i j i = 3 , j = 3 ∂ C ∂ a i j l ∂ a i j l ∂ a k , v l − 1 a k , v l − 1 ∂ z k , v l − 1

而由于

alij=max(al−1mn)=al−1imax,jmax,imax,jmax代表alij对应的pool核区域最大的那个元素的索引 a i j l = m a x ( a m n l − 1 ) = a i m a x , j m a x l − 1 , i m a x , j m a x 代 表 a i j l 对 应 的 p o o l 核 区 域 最 大 的 那 个 元 素 的 索 引

所以:

δl−1k,v=∑iji=3,j=3{[(k=imax,v=jmax)?(∂C∂alij∂alij∂zl−1imax,jmax):0]al−1k,v∂zl−1k,v}=∑iji=3,j=3{(k=imax,v=jmax)?∂C∂alij:0]σ′(zl−1k,v)} δ k , v l − 1 = ∑ i j i = 3 , j = 3 { [ ( k = i m a x , v = j m a x ) ? ( ∂ C ∂ a i j l ∂ a i j l ∂ z i m a x , j m a x l − 1 ) : 0 ] a k , v l − 1 ∂ z k , v l − 1 } = ∑ i j i = 3 , j = 3 { ( k = i m a x , v = j m a x ) ? ∂ C ∂ a i j l : 0 ] σ ′ ( z k , v l − 1 ) }

为方便书写,这里直接用了三目运算符了:D

为了统一敏感度图公式,如果设 ali,j=zli,j=alimax,jmax a i , j l = z i , j l = a i m a x , j m a x l
那么池化层的敏感度图 δl=∂C∂zl=∂C∂al δ l = ∂ C ∂ z l = ∂ C ∂ a l
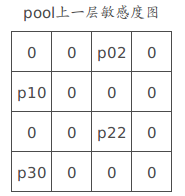
设一直pool层敏感度图如下:

那么pool上一层敏感度图为:

其中:

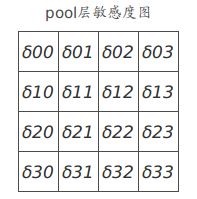
p10=(δ00+δ01+δ10+δ20+δ21)σ′(zl−110)p02=δ02+δ03σ′(zl−102)p22=δ11+δ12+δ13+δ22+δ23+δ31+δ32+δ33σ′(zl−122)p30=δ30σ′(zl−130) p 10 = ( δ 00 + δ 01 + δ 10 + δ 20 + δ 21 ) σ ′ ( z 10 l − 1 ) p 02 = δ 02 + δ 03 σ ′ ( z 02 l − 1 ) p 22 = δ 11 + δ 12 + δ 13 + δ 22 + δ 23 + δ 31 + δ 32 + δ 33 σ ′ ( z 22 l − 1 ) p 30 = δ 30 σ ′ ( z 30 l − 1 )

avg pool

同样设
ali,j=zli,j=alimax,jmax a i , j l = z i , j l = a i m a x , j m a x l
敏感度图: δl=∂C∂zl=∂C∂al δ l = ∂ C ∂ z l = ∂ C ∂ a l

设当前pool层敏感度图为:

所以上一层的敏感度图:

δl−1k,v=∑iji=2,j=2∂C∂alij∂alij∂al−1k,v∂al−1k,v∂zl−1k,v δ k , v l − 1 = ∑ i j i = 2 , j = 2 ∂ C ∂ a i j l ∂ a i j l ∂ a k , v l − 1 ∂ a k , v l − 1 ∂ z k , v l − 1

即:

...δl−100=19δl00σ′(zl−100)δl−101=19δl00σ′(zl−101)+19δ01σ′(zl−101)δl−133=19δl33σ′(zl−133) δ 00 l − 1 = 1 9 δ 00 l σ ′ ( z 00 l − 1 ) δ 01 l − 1 = 1 9 δ 00 l σ ′ ( z 01 l − 1 ) + 1 9 δ 01 σ ′ ( z 01 l − 1 ) . . . δ 33 l − 1 = 1 9 δ 33 l σ ′ ( z 33 l − 1 )

自己推到过,才发现网上所述略有误差