数据结构与算法(c++)--拓扑排序
这次来说一下拓扑排序的东西,仍是基于自己看的资料进行整理的(《数据结构与算法分析c++描述》这本书真的好,强烈推荐)。
拓扑排序是对有向无环图的顶点的一种排序,它使得如果存在一条从Vi到Vj的路径,那么在排序的时候Vj将会出现在Vi的后面。举个例子说,对于有向边(Vi,Vj)而言,在排序的时候,无论如何进行排序选择,最终Vi必定出现在Vj的前面,所以说,拓扑排序的图必须是无环图,试想一下,如果存在一个环的话,那么久必定会出现两个顶点v和w,v先于w的同时w又先于v,这肯定是不可能的。
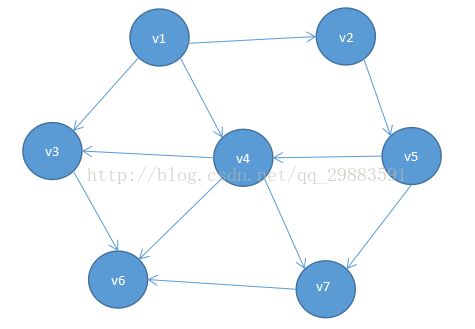
下面举一个例子,如下图所示:
对于上图所示的的有向无环图中,v1,v2,v5,v4,v3,v7,v6和v1,v2,v5,v4,v7,v3,v6都是拓扑排序。由此可以看出,排序不必是唯一的,任何合理的排序都是可以的。
一个简单的求拓扑排序的算法是先找到任意一个没有入边(没有入边的意思是这个顶点没有其他的顶点指向它,即没有指向它的边存在)的顶点,然后显示出该顶点,并将它和它的边一起从图中删除。然后,对图中的其余任何部分应用同样的方法处理。
书上提供了一个简单的伪代码,如下:
void Graph::topsort()
{
for(int counter=0;counter下面给出一个处理的代码:
#include
using namespace std;
#include
#include
#include
#include
#include
#include
template
class ALGraph
{
private:
template
struct Edge
{
int nDestVertex; //邻接顶点编号
weight edgeWeight; //边权重
Edge *pNextEdge; //下一条边
Edge(int d,weight w,Edge *p=NULL):nDestVertex(d),edgeWeight(w),pNextEdge(p){}
};
template
struct Vertex
{
vertexNametype vertexName; //顶点名
Edge *pAdjEdges; //邻接边链表
Vertex( const vertexNametype &name=vertexNametype(),Edge *p=NULL):vertexName(name),pAdjEdges(p){}
};
public:
explicit ALGraph():m_vertexArray(NULL){}
~ALGraph()
{
for(auto it=m_vertexArray.begin();it!=m_vertexArray.end();++it)
{
Edge *p=it->pAdjEdges;
while(NULL!=p)
{
it->pAdjEdges=p->pNextEdge;
delete p;
p=it->pAdjEdges;
}
}
if(!m_vertexArray.empty())
m_vertexArray.clear();
}
bool insertAVertex(const vertexNametype &vertexName) //插入节点
{
int index=getVertexIndex(vertexName);
if(-1!=index)
{
cerr << "点" << vertexName << "已经存在" << endl;
return false;
}
Vertex vertexInstance(vertexName);
m_vertexArray.push_back(vertexInstance);
return true;
}
bool insertAEdge(const vertexNametype &vertexName1,const vertexNametype &vertexName2,const weight &edgeWeight=1) //插入边
{
int index1=getVertexIndex(vertexName1);
if(-1==index1)
{
cerr << "不存在点" << vertexName1 << endl;
return false;
}
int index2=getVertexIndex(vertexName2);
if(-1==index2)
{
cerr << "不存在点" << vertexName2 << endl;
return false;
}
Edge *p=m_vertexArray[index1].pAdjEdges;
while(p!=NULL&&p->nDestVertex!=index2)
{
p=p->pNextEdge;
}
if(NULL==p)
{
p=new Edge(index2,edgeWeight,m_vertexArray[index1].pAdjEdges);
m_vertexArray[index1].pAdjEdges=p; //将p插入到链表开始处
return true;
}
if(p->nDestVertex==index2)
{
Edge *q=p;
p=new Edge(index2,edgeWeight,q->pNextEdge);
q->pNextEdge=p;
return true;
}
return false;
}
bool edgeExist(const vertexNametype &vertexName1,const vertexNametype &vertexName2) const //判断便是否存在
{
int index1=getVertexIndex(vertexName1);
if(-1==index1)
{
cerr << "不存在点" << vertexName1 << endl;
return false;
}
int index2=getVertexIndex(vertexName2);
if(-1==index2)
{
cerr << "不存在点" << vertexName2 << endl;
return false;
}
Edge *p=m_vertexArray[index1].pAdjEdges;
while(p!=NULL&&p->nDestVertex!=index2)
{
p=p->pNextEdge;
}
if(NULL=p)
{
cerr << "不存在" << endl;
return false;
}
if(p->nDestVertex==index2)
{
cout << "存在" << endl;
cout << vertexName1 << ":" ;
while(p!=NULL&&p->nDestVertex==index2)
{
cout << "(" << vertexName1 << "," << vertexName2 << "," << p->edgeWeight << ")" ;
p=p->pNextEdge;
}
cout << endl;
return true;
}
}
void printVertexAdjEdges(const vertexNametype &vertexName) const //输出邻接表
{
int index=getVertexIndex(vertexName);
if(-1==index)
{
cerr << "不存在点" << vertexName << endl;
return ;
}
Edge *p=m_vertexArray[index].pAdjEdges;
cout << vertexName << ":" ;
while(p!=NULL)
{
cout << "(" << vertexName << "," << getData(p->pNextEdge) << p->edgeWeight << ")" ;
}
cout << endl;
}
bool removeAEdge(const vertexNametype &vertexName1,const vertexNametype &vertexName2,const weight &edgeWeight) //删除边
{
int index1=getVertexIndex(vertexName1);
if(-1==index1)
{
cerr << "不存在点" << vertexName1 << endl;
return false;
}
int index2=getVertexIndex(vertexName2);
if(-1==index2)
{
cerr << "不存在点" << vertexName2 << endl;
return false;
}
Edge *p=m_vertexArray[index1].pAdjEdges;
Edge *q=NULL;
while(p!=NULL&&p->nDestVertex!=index2)
{
q=p; //用q记下将要删除的边的前面的边
p=p->pNextEdge;
}
if(NULL==p)
{
cerr << "不存在点" << vertexName1 << "到" << vertexName2 << "的点" << endl;
return false;
}
while(p!=NULL&&edgeWeight!=p->edgeWeight&&p->nDestVertex==index2)
{
q=p;
p=p->pNextEdge;
}
if(p->nDestVertex!=index2)
{
cerr << "不存在点" << vertexName1 << "到" << vertexName2 << "的点" << endl;
return false;
}
if(NULL==q)
m_vertexArray[index1].pAdjEdges=p->pNextEdge;
else
q->pNextEdge=p->pNextEdge;
delete p;
return true;
}
int getVertexIndex(const vertexNametype &vertexName) const //获取顶点索引
{
for(int i=0;i &graphInstance)
{
int vertexNum=graphInstance.getVertexNumber();
out << "这个图有" << vertexNum << "个点" << endl;
for(int i=0;i *p=graphInstance.m_vertexArray[i].pAdjEdges;
while(NULL!=p)
{
out << "(" << vertexName << "," << graphInstance.getData(p->nDestVertex) << "," << p->edgeWeight << ")";
p=p->pNextEdge;
}
out << endl;
}
return out;
}
list topologicialSort() const
{
list vertexList;
vector indegree(m_vertexArray.size(),0);
queue > zeroIndegree;
for(int i=0;i *p=m_vertexArray[i].pAdjEdges;
while(NULL!=p)
{
++indegree[p->nDestVertex];
p=p->pNextEdge;
}
}
for(int i=0;i v=zeroIndegree.front();
zeroIndegree.pop();
vertexList.push_back(v.vertexName);
Edge *p=v.pAdjEdges;
while(NULL!=p)
{
if(--indegree[p->nDestVertex]==0)
zeroIndegree.push(m_vertexArray[p->nDestVertex]);
p=p->pNextEdge;
}
}
if(vertexList.size() prev)
{
int beginIndex=getVertexIndex(beginVertex);
int endIndex=getVertexIndex(endVertex);
printPath(beginIndex,endIndex,prev);
}
private:
vector > m_vertexArray;
vertexNametype getData(int index) const //取顶获点名
{
return m_vertexArray[index].vertexName;
}
void printPath(int beginIndex,int endIndex,const vector prev)
{
if(beginIndex!=endIndex)
printPath(beginIndex,prev[endIndex],prev);
cout << m_vertexArray[endIndex].vertexName << " " ;
}
Edge *getEdge(int begin,int end)
{
Edge *p=m_vertexArray[begin].pAdjEdges;
while(NULL!=p)
{
if(p->nDestVertex==end)
break;
p=p->pNextEdge;
}
return p;
}
};
int main()
{
ALGraph graph;
graph.insertAVertex("v1");
graph.insertAVertex("v2");
graph.insertAVertex("v3");
graph.insertAVertex("v4");
graph.insertAVertex("v5");
graph.insertAVertex("v6");
graph.insertAVertex("v7");
graph.insertAEdge("v1","v2");
graph.insertAEdge("v1","v4");
graph.insertAEdge("v1","v3");
graph.insertAEdge("v2","v4");
graph.insertAEdge("v2","v5");
graph.insertAEdge("v3","v6");
graph.insertAEdge("v4","v7");
graph.insertAEdge("v4","v6");
graph.insertAEdge("v4","v3");
graph.insertAEdge("v5","v7");
graph.insertAEdge("v7","v6");
cout << graph << endl;
list result=graph.topologicialSort();
cout << "拓扑排序的结果为:"<< endl;
for(auto it=result.begin();it!=result.end();++it)
cout << *it << " " ;
cout << endl;
return 0;
}
对于上面的代码可能看起来会有点多啊,其实我们在平时解题的时候,很多情况下不会用到这么复杂的,原因之一就是类的运用啊,因为一旦使用了类,不可避免的就会产生很多的代码,尤其是在进行各种方法之间的优化的时候。在这个程序中,我使用了邻接表的方法对图进行处理的,在很多情况下也可以使用矩阵的方法进行处理,这两种方法各有优劣,分别对应于稀疏和稠密类型的图很有效果,这里因为是基于c++的嘛,就给出了一个运用类进行构造的例子,并且采用邻接表进行,相对来说矩阵方法更加简单易写,这里就不给出了。
至于代码量而言,其实如果仅仅是写这一个算法的话,确实是有点小题大做了,毕竟就一个那么简答的算法实现,没有必要搞个300多行出来,太吓人了吧,其实这是为了其它算法铺路的,在后续的博客中会看到,这些都是通用的东西,所以这个类模型可以把很多种算法整合到一起,而共用很多的代码,后面会继续看到。