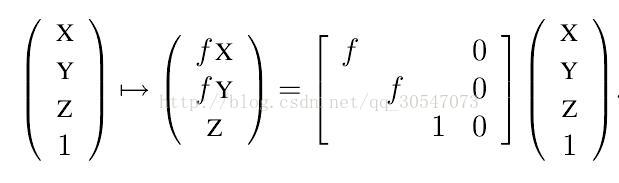计算机视觉与摄影测量的不同
嘛,本人第一次写博客嘛,当然要干货满满才行。
学术上称不上有什么造诣,但是也有自己的心得。相比抄袭来讲,我还是更喜欢原创。无论是什么东西,只有加入了自己的思考才会变得活跃。
虽说计算机视觉与摄影测量是不分家的,但是同时验证这两种理论体系的的我倒是从来没见过,也从没见过有人分析他们的区别。
那么今天来对比一下摄影测量和计算机视觉的不同。
有人说计算机视觉与摄影测量是一个东西。
我同意。
严格的来讲,计算机视觉和近景摄影测量是一个东西。
他们几乎是在解决相同的问题,但用的是不同的手段。这一次呢,主要聊一下位姿估计。
在位姿估计中,摄影测量与计算机视觉有何不同呢?
我们先看摄影测量学。
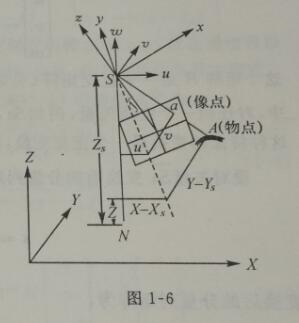
让我们翻开《近景摄影测量原理》第五页,就可以看到摄影测量所用的数学模型了。对啦,就是图1-6.
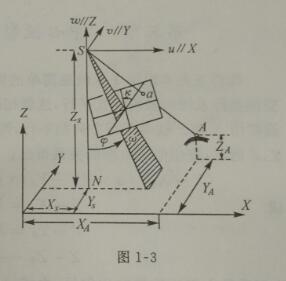
而图1-3显示了摄影测量的旋角系统。这张图非常关键,它显示了与计算机视觉不同的关键。
那么对于旋角系统的说明我们也贴上。没错,就是我们熟知的phi、omega、kappa系统。你需要记住的是,这个坐标系是一个右手系,它的旋转方向为:
1.以Y轴为正方向顺时针旋转phi
2.以X轴为正方向逆时针旋转omega
3.以Z轴为正方向逆时针旋转kappa
为什么我要强调正方向与顺逆?因为不同的理论体系对应的旋角系统是完全不一样的。比如有的国外的学术论文中花了很多篇幅先介绍一通自己的旋角系统,我们也许图个省事就空过去不看了,结果照着别人的文章做,说做不出来,和别人结果就是有差距,但就是不知道问题在哪里。那么有可能别人的理论体系就只在它的旋角系统下生效。这一点在摄影测量中已经很明显了,它的旋角并非都是顺时针和逆时针,而是既有顺时针旋转也有逆时针旋转。
再者,摄影测量学中的内定向与计算机视觉中的内定向也是不同的,这就造成它们的输入数据不同。这一点后面也会讲到。
那下面我们再看一下计算机视觉的旋角系统
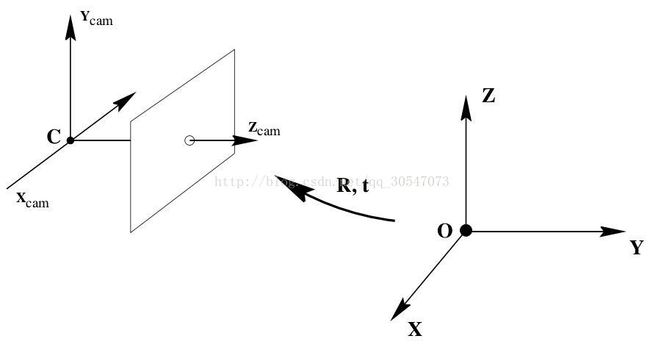
那我就直接用《Multiview Geometry in Compute vision》这本书的内容了。
好,这两张图都是小孔成像模型,没毛病。我们接着看。
好那么问题来了,这里的R,T是什么它竟然没说清楚,究竟是怎么旋转的也没说清楚,但我通过后期的实验可以告诉你,它是以Z轴为主轴的一个旋转矩阵。
那么什么叫以Z轴为主轴呢?我们知道,一个旋转矩阵只是一个旋转方式而已,它本身并不能代表一个方向,而一个向量却可以。我们想得到相机的方向,就是用这个矩阵R左乘以(0,0,1)这个向量就可以了。然而,摄影测量中的主轴是什么呢?我通过实验告诉你,是(0,0,-1)。为什么差一个负号呢?
这就是它们模型之间的差别了。这就必须要说到它们的内定向。
摄影测量中输入的数据为(x,y,-f)x与y分别为像素坐标,f为以毫米为单位的焦距。内定向公式我用代码写出来:
xy_f(i, 0) = (xy_fPic(i, 0) - IMGW / 2)*CCDW;
xy_f(i, 1) = (IMGH / 2 - xy_fPic(i, 1))*CCDW;
xy_f(i, 2) = -f;//所有单位均为毫米这样你可以看到,以图像左上角为原点的像素为单位的像素坐标系转换到了以中心为坐标原点单位为毫米的图像中心坐标系,同时坐标轴进行了反转。
而计算机视觉中的内定向又是什么样的呢?是用K矩阵的逆乘以(x,y,1)这个齐次坐标,x,y并没有换算为以毫米为单位,相反,为了保证单位统一它将K矩阵中的f换算成了以像素为单位。当然,在相片的CCD宽度一致的情况下,这个以像素为单位的焦距fpixcel是可以求出来的。其过程就如同下图所示了。到这里,做过类似研究的人就应该明白了,为何自己的矩阵总是求不对。因为摄影测量与计算机视觉严格来说只能说是相似而已,它们之间的去别还是很明显的。
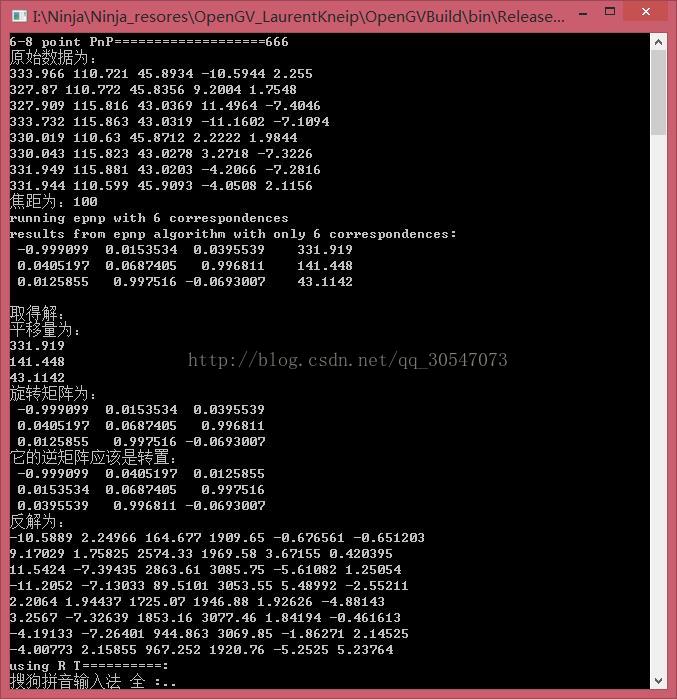
为了让这个说说说更有说服力,我下面将我的实测数据放上来,让大家感受一下摄影测量与计算机视觉的对比。
本人分别用计算机视觉中的DLT算法与Epnp解算P矩阵,再用奇异值分解的方法求出RT,与用EPnp求出的摄影测量矩阵进行对比。
选取了8对2D-3D点,全部参与运算。
第一幅图是用Epnp求出的摄影测量矩阵。反投影误差是符合预期的。利用它进行的贴图效果完全正确。
第二幅图是用DLT结果。
我们抛却所有。我们仔细对比一下结果就会发现,摄影测量R矩阵与计算机视觉R矩阵看起来是相互转置的关系。然而眉头一皱,没有这么简单,中间还差几个负号。
他们的绝对值倒是相差不远。这恐怕是因为计算机视觉的矩阵在旋转的时候都是默认全部是顺时针或者是逆时针,而摄影测量中旋转的时候有顺有逆。小伙伴们懵逼了?没有关系。你只要记住,造成摄影测量与计算机不同的因素在于两套理论体系在构成旋转矩阵的时候有所不同,并且内定向的时候也各不相同就行了。
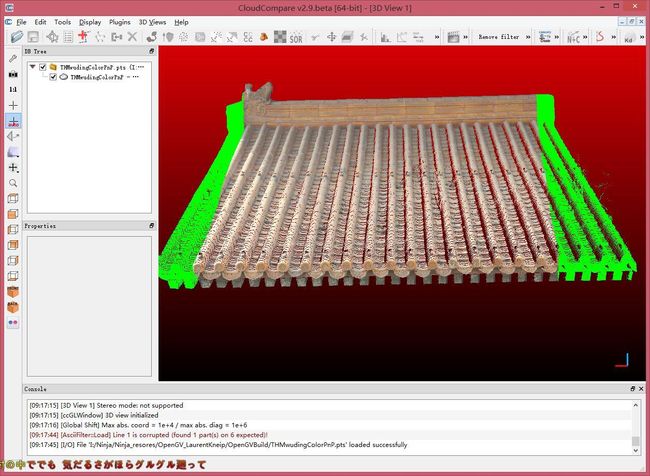
下面我放一个贴图效果来给大家看看。顺带说一句,这两种方法所达成的贴图效果是一样的,都很精确。那么我就只放一组贴图效果上来就行了。
修正:在第二个控制台中显示了原始的T与-RT的结果,之所以要乘以-RT是为了将相机光心变换到世界坐标系下,但是实际上应该是-R.inverse()T,也就是-R的转置再乘以T才能得到正确结果,正确结果应该为331,144,34才对。