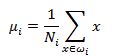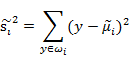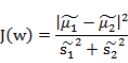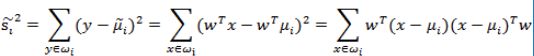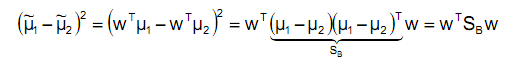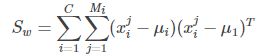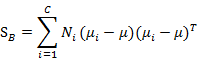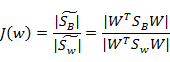人脸识别算法二：Fisherface（LDA）

  LDA线性判别分析

      也称FLD（Fisher线性判别）是一种有监督的学习方法（supervised learning）。目的：是从高维空间中提取出最优判别力的低维特征，这些特征使同一类别的样本尽可能的靠近，同时使不同类别的样本尽可能的分开，即选择使样本的类间散布矩阵和类内散布矩阵达到最大比值的特征。因此，用FLD得到的特征不但能够较好的表示原始数据，而且更适合分类。

         Fisherface是由Ronald Fisher发明的，Fisherface所基于的LDA（Linear Discriminant Analysis，线性判别分析）理论和特征脸里用到的PCA有相似之处，都是对原有数据进行整体降维映射到低维空间的方法。

为什么要用LDA

     PCA是常用的有效的数据降维的方法，与之相同的是LDA也是一种将数据降维的方法。PCA已经是一种表现很好的数据降维的方法，那为什么还要有LDA呢？下面我们就来回答这个问题？ 
     PCA是一种无监督的数据降维方法，与之不同的是LDA是一种有监督的数据降维方法。我们知道即使在训练样本上，我们提供了类别标签，在使用PCA模型的时候，我们是不利用类别标签的，而LDA在进行数据降维的时候是利用数据的类别标签提供的信息的。 
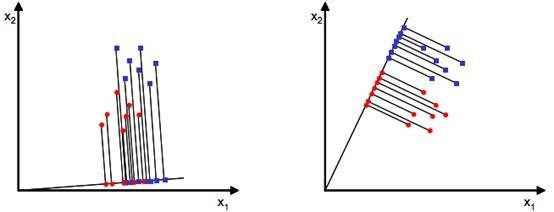
      从几何的角度来看，PCA和LDA都是讲数据投影到新的相互正交的坐标轴上。只不过在投影的过程中他们使用的约束是不同的，也可以说目标是不同的。PCA是将数据投影到方差最大的几个相互正交的方向上，以期待保留最多的样本信息。样本的方差越大表示样本的多样性越好，在训练模型的时候，我们当然希望数据的差别越大越好。这就是PCA降维的目标：将数据投影到方差最大的几个相互正交的方向上。这种约束有时候很有用，比如在下面这个例子：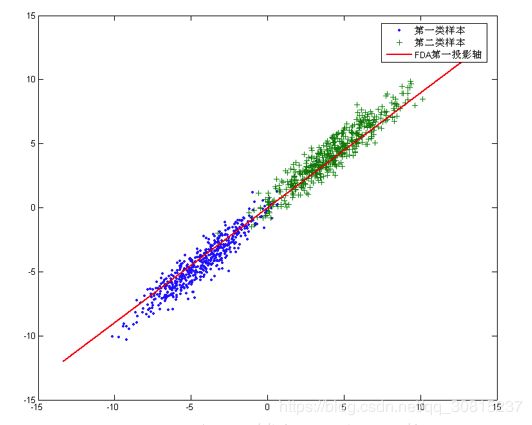

图中红色直线所在的方向。也是数据样本做投影，方差最大的方向。向这个方向做投影，投影后数据的方差最大，数据保留的信息最多。 
但是，对于另外的一些不同分布的数据集，PCA的这个投影后方差最大的目标就不太合适了。比如对于下面图片中的数据集：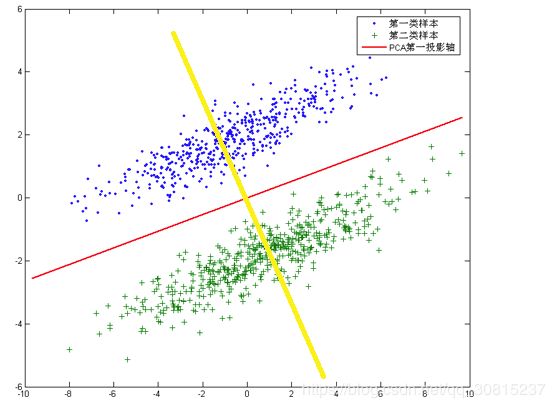

图中还有一条耀眼的黄色直线，向这条直线做投影即能使数据降维，同时还能保证两类数据仍然是线性可分的。上面的这个数据集如果使用LDA降维，找出的投影方向就是黄色直线所在的方向。 
这其实就是LDA的思想，或者说LDA降维的目标：将带有标签的数据降维，投影到低维空间同时满足三个条件：

• 尽可能多地保留数据样本的信息（即选择最大的特征是对应的特征向量所代表的的方向）。
• 寻找使样本尽可能好分的最佳投影方向。
• 投影后使得同类样本尽可能近，不同类样本尽可能远。

1、数据集是二类情况

       通常情况下，待匹配人脸要和人脸库内的多张人脸匹配，所以这是一个多分类的情况。出于简单考虑，可以先介绍二类的情况然后拓展到多类。假设有二维平面上的两个点集（x是包含横纵坐标的二维向量），它们的分布如下图（分别以蓝点和红点表示数据）：

                       

       原有数据是散布在平面上的二维数据，如果想用一维的量（比如到圆点的距离）来合理的表示而且区分开这些数据，该怎么办呢？一种有效的方法是找到一个合适的向量w（和数据相同维数），将数据投影到w上（会得到一个标量，直观的理解就是投影点到坐标原点的距离），根据投影点来表示和区分原有数据。我们将这个最佳的向量称为w（d维），那么样例x（d维）（此处d=2）到w上的投影可以用下式来计算（投影点到到原点的距离）：

                                                                                   

      上图给出了两种w方案，w以从原点出发的直线来表示，直线上的点是原数据的投影点。直观判断右侧的w更好些，其上的投影点能够合理的区分原有的两个数据集。但是计算机不知道这些，所以必须要有确定的方法来计算这个w。

从直观上来看，右图比较好，可以很好地将不同类别的样本点分离。

     接下来我们从定量的角度来找到这个最佳的w。

1、首先计算每类数据的均值（中心点）：

                                                       

这里的i是数据的分类个数，代表某个分类下的数据点数，比如 代表红点的中心， 代表蓝点的中心。

2、数据点投影到w上的中心为：

                                                     

如何判断向量w最佳呢，可以从两方面考虑：

                          1、不同的分类得到的投影点要尽量分开；

                          2、同一个分类投影后得到的点要尽量聚合。

从这两方面考虑，可以定义如下公式：

                                               

                                                   

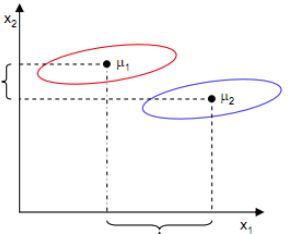
1、J(w)代表不同分类投影中心的距离，它的值越大越好。

2、称之为散列值（scatter matrixs），代表同一个分类投影后的散列值，也就是投影点的聚合度，它的值越小代表投影点越聚合。(投影在特征向量上的点，与投影中心的距离差的平方和)

只考虑J(w)行不行呢？不行，看下图：

                                                     

       样本点均匀分布在椭圆里，投影到横轴x1上时能够获得更大的中心点间距J(w)，但是由于有重叠，x1不能分离样本点。投影到纵轴x2上，虽然J(w)较小，但是能够分离样本点。因此我们还需要考虑样本点之间的方差，方差越大，样本点越难以分离。

      所以要结合散列值结合两个公式，第一个公式做分子另一个做分母：

                                                              

    上式是w的函数，值越大，说明w降维性能越好，所以下面的问题就是求解使上式取最大值的w。

这正是LDA的基本思想是：

找到一个最佳的判别矢量空间w，使得投影到该空间的样本的类间离散度与类内离散度比达到最大。

如何求解？

把散列函数展开：

                                       

我们定义上式中中间那部分

                                       

     这个公式的样子不就是未除以样例数的协方差矩阵么，称为散列矩阵（scatter matrices），这就是原数据的散列矩阵了，对于固定的数据集来说，它的散列矩阵也是确定的。

   我们定义为类内散列矩阵：   , 回到上面的公式,并用做替换，得到：                                         

                                                            

                                                         

展开J(w)的分子并定义，称为类间散列矩阵。

                         

这样就得到了J(w)的最终表示：

                                                                 

上式求极大值可以利用拉格朗日乘数法， 在我们求导之前，需要对分母进行归一化，因为不做归一的话，w扩大任何倍，都成立，我们就无法确定w。怎么确定最好的w呢。

可以令，利用拉格朗日乘数法得到：

                                                

w是矩阵,求导时可以简单地把当做看待。如果可逆，那么将求导后的结果两边都乘以，得

                                                  

可以发现w其实就是矩阵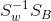的特征向量。我们把w求解问题转化为了求解特征向量。

通过上式求解w还是有些困难的，而且w会有多个解，考虑下式：

                                                 

将其带入下式：

                            

其中是以w为变量的数值，因为(u1-u2)^T和w是相同维数的，前者是行向量后者列向量。继续带入以前的公式：

 代入最后的特征值公式得

                                

  由于对w扩大缩小任何倍不影响结果，因此可以约去两边的未知常数和，得到

                                                           

我们只需要求出原始样本的均值和方差，（为类内散列矩阵）就可以求出最佳的方向w。

2、数据集是多类的情况

     假设有C个人的人脸图像，每个人可以有多张图像，所以按人来分，可以将图像分为C类，这节就是要解决如何判别这C个类的问题。判别之前需要先处理下图像，将每张图像按照逐行逐列的形式获取像素组成一个向量，和第一节类似设该向量为，设向量维数为n(像素数)，设x为n*1的列向量。这里的n有可能成千上万，比如100x100的图像得到的向量为10000维，所以第一节里将x投影到一个向量的方法可能不适用了，比如下图：

                                            

      平面内找不到一个合适的向量，能够将所有的数据投影到这个向量而且不同类间合理的分开。所以我们需要增加投影向量w的个数（当然每个向量维数和数据是相同的，不然怎么投影呢），假设我们有C个类别，需要k维向量（或者叫做基向量）来做投影：.

     是n维的列向量，所以W是个n*k的矩阵，这里的k其实可以按照需要随意选取，只要能合理表征原数据就好。

我们将样本点在这k维向量投影后结果表示为，有以下公式成立

                                                           

                                                           

所以这里的y是k维的列向量。

像上一节一样，我们将从投影后的类间散列度和类内散列度来考虑最优的w，考虑图（2）中二维数据分为三个类别的情况。与第一节类似，依然代表类别i的中心，而定义如下：

                                                    

其中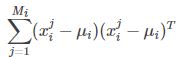：   ：表示第i类样本的协方差矩阵。所以就是表示C类样本协方差矩阵之和。它是一个n*n的矩阵。

所有x的中心μ定义为：

                                            

类间散列度，表示各个类样本均值的协方差矩阵。定义和上一节有较大不同：

                                  

代表的是每个类别到μ距离的加和，注意代表类别i内x的个数，也就是同一个人的人脸图像个数。

上面的讨论都是投影之间的各种数据，而J(w)的计算实际是依靠投影之后数据分布的，所以有：

                                                                       

                                          

上式分别代表投影后的类别i的中心，所有数据的中心，类内散列矩阵，类间散列矩阵。

与上节类似J(w)可以定义为：

                                        

                                         

        回想我们上节的公式J(w)，分子是两类中心距，分母是每个类自己的散列度。现在投影方向是多维了（好几条直线），分子需要做一些改变，我们不是求两两样本中心距之和（这个对描述类别间的分散程度没有用），而是求每类中心相对于全样本中心的散列度之和。得到：

                                

最后化为：

                                       

最终转化为求解矩阵的特征向量，然后根据需求取前k个特征值最大的特征向量。

进行人脸识别时，将人脸向量投影到LDA子空间w，得到一个低维向量 : ,其中 

注意： 这里的求逆的前提是满秩矩阵，但实际计算时，如何呢？

是一个p*p的矩阵。在LDA算法中，当特征维度p十分大(p>样本数−类别数)的时候得出的协方差矩阵不可逆。

我们通常有2个办法解决该问题：

解决方法一： 
令, 其中γ是一个特别小的数，这样一定可逆。 
解决方法二： 
先使用PCA对数据进行降维，使得在降维后的数据上可逆，再使用LDA。

      协方差与样本矩阵A有相同的秩,协方差的秩必须是P才能满秩。而Rank(A)=min(p,样本数−类别数)。显然，如果p>N−K，矩阵非满秩，因此不可逆。然而不必惊慌，PCA这个原生态的降维手段总可以让过程进行下去。只要将图像的特征维度p缩减到N−K或以下即可.这也是为什么博客https://blog.csdn.net/qq_30815237/article/details/89185371 中Fisher线性判别分析:中train函数的源码中出现

if((_num_components <= 0) || (_num_components > (C-1)))
        _num_components = (C-1);
    // perform a PCA and keep (N-C) components
    PCA pca(data, Mat(), PCA::DATA_AS_ROW, (N-C));
    // 将样本投影到主成分的特征图最为输入，计算它的LDA向量，构造 LDA on it，注意这里输入的不是原图
    LDA lda(pca.project(data),labels, _num_components);

from :https://blog.csdn.net/zhaoyu775885/article/details/80176089

另外还需注意：

     由于中的 秩为1，因此的秩至多为C（矩阵的秩小于等于各个相加矩阵的秩的和，C是类别个数）。由于知道了前C-1个后，最后一个可以有前面的来线性表示，

     因此的秩至多为C-1。那么K最大为C-1。特征值大的对应的特征向量分割性能最好。那么至多可以取到N-1个特征向量来表征原数据。即：LDA至多可生成C-1维子空间

      大家知道PCA里求得的特征向量都是正交的（因为协方差矩阵是对称矩阵），但是这里的并不是对称的，所以求得的K个特征向量不一定正交，这是LDA和PCA最大的不同。求特征向量不能采用奇异值分解的方式，而因该采用更通用的求一般方阵特征向量的方式，（像矩阵论里学的方法来求，例如下：）

                                      

     降维之后如何根据y值来判别分类呢？取[y1,y2,...,yk]中最大的那个就是所属的分类。对于有C个类别的分类问题，我们最多只能分出C-1个类别来.如前所述，如果在一组人脸集合上，求得k个特征向量，还原为人脸图像的话，就像下面这样：

                                  

      得到了k个特征向量，如何匹配某人脸和数据库内人脸是否相似呢，方法是将这个人脸在k个特征向量上做投影，得到k维的列向量或者行向量，然后和已有的投影求得欧式距离，根据阈值来判断是否匹配。需要说明的是，LDA和PCA两种方法对光照都是比较敏感的，如果你用光照均匀的图像作为依据去判别非均匀的，那基本就惨了。

3、Opencv中的LDA

3.1、LDA的两个基本用途：

降维和分类器（例如OpenCV中将LDA和K邻近分类器封装为一个“分类器”，这里K=1。所以本质还是降维和使数据易于可分）

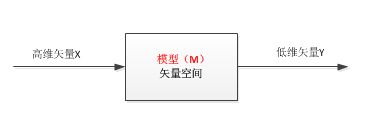
1）训练模型

                               

1. 数据(D):高维特征矢量
2. 训练(T):操作模式
3. 规则(R):训练数据的规则
4. 黑盒子(B):如果我们只是想应用而不想理解其内部的复杂原理，我们可以不关系黑盒子里面是如何操作的。
5. 模型(M):训练的结果，即产生(P)一个模型，这里是上面描述的一个矢量空间。

2）将高维数据送入模型实现降维

                                                    

3.2、LDA分类器思想：

    这里的分类思想，是OpenCV一种封装的分类思想，OpenCV在人脸识别算法中将LDA+(K=1)邻近分类器组合，构造所谓的“合成分类器”，相当于类中的封装。

1）将所有训练样本图像投影到LDA子空间

2）将测试图像投影到LDA子空间

3）找到投影后的训练样本集和测试图像之间的最邻近，即如果测试图像与训练样本中的b最邻近，b属于C类，那么测试图像也属于C类。

3.3、LDA代码

OpenCV为我们实现了LDA类，LDA类的构造函数：

LDA(const Mat& src, vector labels,int num_components = 0):_num_components(num_components)  
       {  
           this->compute(src, labels); //! compute eigenvectors and eigenvalues  
       }  

1. 矩阵src以行存储训练样本矢量，行数表示训练样本的总数，列数表示样本矢量（特征矢量）的维数
2. abels是与训练样本所对应的类别。此构造函数要求输入数据格式严格。
3. 参数num_components=0采用默认，由给定数据自动判决

LDA::project

投影样本到LDA子空间

// Projects samples into the LDA subspace.  
Mat LDA::project(InputArray src) {  
   return subspaceProject(_eigenvectors, Mat(), _dataAsRow ? src : src.getMat().t());  
}  

3.4、应用降维思路：

训练数据的处理：

1、循环读入训练图像Mat，并将Mat对象存储到vector容器中，同时新建一个Mat对象，或行矢量或列矢量来存储类别标签。

2、将步骤1中的数据传入到LDA的构造函数中，构造函数进行计算处理，从而获得特征矢量。

3、将训练数据利用project函数，投影到特征矢量构造的子空间，即LDA子空间，将返回的Mat矢量保存起来，做后续的处理。

4、将LDA对象，利用save保存起来。

测试数据的处理：

1、利用load函数将LDA导入

2、利用project函数，将测试数据投影到LDA子空间，保存返回的Mat矢量，做后续的处理。

4、PCA+LDA

      原始样本采用了200*200大小的图片，形成了40000维的特征矢量，其中包含了大量冗余信息和噪声，导致了LDA方法的不准确。因此一般先采用PCA降维：首先对原始样本图像进行PCA降维，而后再使用LDA进行分类训练；在进行测试时，也先对原始图像进行PCA降维，再利用LDA进行识别，这样可以有效消除冗余信息和噪声的干扰，压缩后的信息对脸部位置也变得不敏感。

      转换矩阵，可以将样本投影到c-1维空间，其中c表示类别。

                                                         

                                          投影公式为：

     表示LDA的特征矢量构成的，表示PCA的特征矢量构成的，u是PCA分析中所有样本的均值。z列向量的维数为类别数目-1.注意：这里x是n*1列向量，是 n*(样本数−类别数)矩阵，得到(样本数−类别数)*1的列向量，实际上就是压缩后的人脸图像temp，  (   ，这里的是在pca降维后的人脸图像上求得的投影向量，矩阵尺寸为(样本数−类别数)*（类别数-1）)

     PCA对光照的灵敏度较高。LDA对光照不如PCA对光照的敏感。LDA的性能同样严重的依赖于输入的数据。LDA也可以像PCA那样对图像进行重建，但是LDA重建效果没有PCA好，这是因为PCA利用的个体的主成份特征，而LDA利用了辨别个体之间不同的特征。Fisher face方法(PCA+LDA)在OpenCV中的实现请参考：OpenCV人脸识别类FaceRecognizer

from：https://blog.csdn.net/zhazhiqiang/article/details/21189415

from：https://blog.csdn.net/smartempire/article/details/23377385

from：http://www.cnblogs.com/jerrylead/archive/2011/04/21/2024384.html

from：https://blog.csdn.net/zdyueguanyun/article/details/8595549

from：https://www.cnblogs.com/txg198955/p/4106682.html

from：https://www.cnblogs.com/engineerLF/p/5393119.html