论文精读之PDE-Net: Learning PDEs from Data

整理人：陈振庭
qq：2621336811
第一次写博客，以后通过博客来记录自己的研究生学习过程。最近研究深度学习在PDE方面的应用，也要开始精读一些英文文章啦~
顺便附上文章的代码：文章中两个案例的代码
摘要
Partial differential equations (PDEs) play a prominent role in many disciplines of science and engineering. PDEs are commonly derived based on empirical observations. However, with the rapid development of sensors, computational power, and data storage in the past decade, huge quantities of data can be easily collected and efficiently stored. Such vast quantity of data offers new opportunities for data-driven discovery of physical laws. Inspired by the latest development of neural network designs in deep learning, we propose a new feed-forward deep network, called PDE-Net, to fulfill two objectives at the same time: to accurately predict dynamics of complex systems and to uncover the underlying hidden PDE models. Comparing with existing approaches, our approach has the most flexibility by learning both differential operators and the nonlinear response function of the underlying PDE model. A special feature of the proposed PDE-Net is that all filters are properly constrained, which enables us to easily identify the governing PDE models while still maintaining the expressive and predictive power of the network. These constrains are carefully designed by fully exploiting the relation between the orders of differential operators and the orders of sum rules of filters (an important concept originated from wavelet theory). Numerical experiments show that the PDE-Net has the potential to uncover the hidden PDE of the observed dynamics, and predict the dynamical behavior for a relatively long time, even in a noisy environment.

1.Introduction

1.1. Related Work

1.2. Our Approach

这篇文章，我们设计了一个深度前馈网络-----PDE-Net ，基于如下的非线性PDE：
$$u_t=F\left(x,u,\nabla u,{\nabla }^{2}u,\dots \right),x\in \Omega \subset R^{2}t\in [0,T]$$PDE-Net的目标是学习非线性函数F和做精确的预测。

2. PDE-Net: A Flexible Deep Archtecture to Learn PDEs from Data

给定一组测量值和一些物理量：$\left\{u(t,\cdot ):t=t_0,t_1,\dots \right\}$，在空间 $\Omega \subset R^2$，且$u(t,\cdot ):\Omega \mapsto R$ , 我们假设观察数据与如下的PDE有关：
$$u_t(t,x,y)=F\left(x,y,u_x,u_y,u_{xx},u_{xy},u_{yy},\dots \right),(1)|$$其中$(x,y)\in \Omega R^2,t\in [0,T]$.
我们的目标是设计一个前馈网络PDE-Net，能够逼近PDE（1）,且
1)我们能够尽可能长时间的预测方程的动态行为；
2)我们能够揭示相应函数F的形式和所涉及的微分算子。
PDE-Net主要由两部分组成：
1)自动确定PDE中所涉及的微分算子；
2)非线性响应函数F的逼近。

2.1. Convolutions and Differentiations

定义2.1 (Order of Sum Rules)
对于一个滤波器$q$，当
$$\sum _{k\in Z^2}{k}^{\beta }q[k]=0(2)$$我们说$q$有求和规则的阶$\alpha =\left({\alpha }_1,{\alpha }_2\right)$且$\alpha \in Z_{+}^2$对于所有$\beta =\left({\beta }_1,{\beta }_2\right)\in Z_{+}^2$且$|\beta |:={\beta }_1+{\beta }_2<|\alpha |$和所有$\beta \in Z_{+}^2$且$|\beta |=|\alpha |$但是$\beta ̸=\alpha$。如果对于（2）有$\beta \in Z_{+}^2$且$|\beta |<\mathrm{K}$但$\beta ̸=\overline{\beta }$，且对某个$\overline{\beta }\in Z_{+}^2$且$|\overline{\beta }|=\mathrm{J}<\mathrm{K}$。那么我们说q有总的求和规则的阶$K\backslash \{J+1\}$.
在实际应用中，滤波器通常是有限的且可以看做是一个矩阵。对于一个$N\ast N$滤波器$q，N$是奇数，假设$q$的索引从$-\frac{N-1}{2}$开始,那么（2）可以写成如下形式$$\sum _{l=-\frac{N-1}{2}}^{\frac{N-1}{2}}\sum _{m=-\frac{N-1}{2}}^{\frac{N-1}{2}}{l}^{{\beta }_1}{m}^{{\beta }_2}q[l,m]=0$$
命题2.1 令$q$是一个有求和规则的阶为$\alpha \in Z_{+}^2$的滤波器,那么对于一个光滑函数$F(x)\text{ on }{R}^2$，我们有:$$\frac{1}{{\epsilon }^{|\alpha |}}\sum _{k\in {\mathbb{Z}}^2}q[k]F(x+\epsilon k)=C_{\alpha }\frac{{\partial }^{\alpha }}{\partial x^{\alpha }}F(x)+O(\epsilon ),as\epsilon \to 0(3)$$如果，另外，$q$有总的求和规则的阶为$K\backslash \{|\alpha |+1\}$且对于有些$K>|\overline{\alpha }|$，那么有$$\frac{1}{{\epsilon }^{|\alpha |}}\sum _{k\in Z^2}q[k]F(x+\epsilon k)=C_{\alpha }\frac{{\partial }^{\alpha }}{\partial x^{\alpha }}F(x)+O\left({\epsilon }^{K-|\alpha |}\right),as\epsilon \to 0(4)$$
根据命题2.1，一个$\alpha$阶的微分算子可以用一个有$\alpha$阶求和规则的滤波器$q$来近似。甚至，根据（4），我们可以得到，一个对于给定的高阶微分算子的对应的滤波器的高阶近似。滤波器的总的求和规则的阶为$K>|\alpha |+k,k\ge 1$比如，考虑这样一个滤波器$$q=\left(\begin{array}{ccc}1& 0& -1\\ 2& 0& -2\\ 1& 0& -1\end{array}\right)$$他的一个求和规则的阶为（1,0），总的求和规则的阶为3{2}，那么Q对应于$\frac{\partial }{\partial x}$的一个二阶离散近似。
现在我们介绍一下矩矩阵的概念。在一个PDE-Net中，对于一个给定的带有约束条件的$N\ast N$滤波器$q，Q$的矩矩阵定义为：$$M(q)={\left(m_{i,j}\right)}_{N\times N}$$其中$m_{i,j}=\frac{1}{(i-1)!(j-1)!}{\sum }_{k\in {\mathbb{Z}}^2}{k}_1^{i-1}{k}_2^{j-1}q\left[k_1,k_2\right]$,$i,j=1,2,\dots ,N$.
结合（5）和命题2.1，我们可以轻松得出，滤波器q能够设计成任意给定任意阶微分算子的近似，通过使用带约束条件的$M（q）$。比如，如果我们想要近似$\frac{\partial u}{\partial x}$,可以用卷积$q\otimes u$，其中$q$是3*3的滤波器，我们可以考虑用如下的带约束的$M（q）$$$\left(\begin{array}{ccc}0& 0& \star \\ 1& \star & \star \\ \star & \star & \star \end{array}\right)\text{ or }\left(\begin{array}{ccc}0& 0& 0\\ 1& 0& \star \\ 0& \star & \star \end{array}\right)(6)$$其中，左边的矩矩阵保证了近似的准确度至少是一阶的，另一个至少是二阶的.特别的，对于一个所有元素都是带约束的$M（q）$，比如$$M(q)=\left(\begin{array}{ccc}0& 0& 0\\ 1& 0& 0\\ 0& 0& 0\end{array}\right)$$其对应的滤波器是被唯一确定的，我们称为冻结滤波器。所有过滤器学习在相关力矩上受到部分约束矩阵。值得注意的是，用于近似的过滤器的近似性质是被他的大小所限制的。大的滤波器可以近似高阶微分算子或具有更高近似阶的低阶微分算子。但是，较大的过滤器会导致更多的内存管理费用和更高的计算成本。这是一种智慧在实践中平衡权衡。

2.2. Architecture of PDE-Net

对于给定的PDE（1）,我们使用向前欧拉做时间的离散。
ONE$\delta t-block$:
令$u\left(t_i+1,\cdot \right)$是$u$在时间$t_{i+1}$上基于$u$在$t_i$上的预测值，那么我们有：$$\tilde{u}\left(t_{i+1},\cdot \right)=D_{0}u\left(t_i,\cdot \right)+\Delta t\cdot F\left(x,y,D_{00}u,D_{10}u,D_{01}u,D_{20}u,\dots \right).(7)$$其中，$D_0,D_{ij}$是卷积算子，可以看做$D_{0}u=q_0\otimes u\text{ and }{D}_{ij}u=q_{ij}\otimes u$, 微分算子的近似$D_{ij}u\approx \frac{{\partial }^{i+j}u}{{\partial }^{i}x{\partial }^{j}y}$.
我们假设PDE的最高阶数小于一些正整数。那么，近似f的任务相当于多元回归问题，就可以用点神经网络来近似了。我们实现了一个（7）的近似框架：$\delta t-block$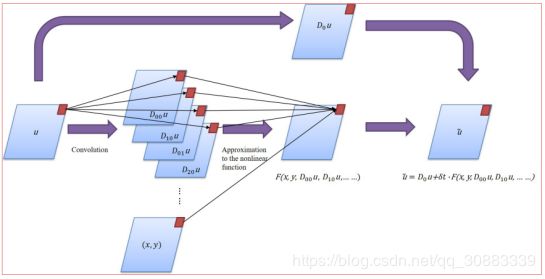
Figure 1. The schematic diagram of a $\delta t-block$

PDE-NET (MULTIPLE $\delta t-blocks$):
一个$\delta t-block$只能保证一步动态变化的准确度，为了能够实现长期的预测，我们搭建了多层$\delta t-blocks$，使之成为一个深层网络，我们叫做PDE-Net。

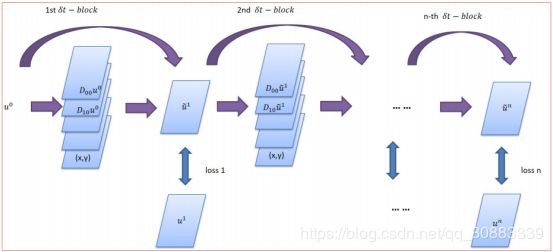
Figure 2. The schematic diagram of the PDE-Net.

PDE-Net可以简单描述为：
1)多个$\delta t-blocks$堆积而成；
2)所有的$\delta t-blocks$共享参数。
对于给定的输入数据$u\left(t_i,\cdot \right)$，训练一个有多层$\delta t-blocks$的PDE-Net需要最小化累计误差${\Vert u\left(t_{i+n},\cdot \right)-u\left(t_{i+n},\cdot \right)\Vert }_2^2$，这里$u\left(t_{i+n},\right)$是基于输入$u\left(t_i,\cdot \right)$的PDE-Net的输出。
LOSS FUNCTION AND CONSTRAINTS:
考虑数据集$\left\{u_j(t,\cdot ):i,j=0,1,\dots \right\}$，这里$j$代表对于某个未知动态初始化条件的第$j$个的结果。我们想要用$n\delta t-blocks$来训练PDE-Net。对于一个给定的$n\ge 1$，每一个数据对$\left\{u_i(t,\cdot ),u_i\left(t_{i+n},\cdot \right)\right\}$，是一个训练样本。这里$u_i\left(t_{i,}\cdot \right)$是输入，$u_{i+n}\left(t_{i,}\cdot \right)$是输出/标签。
我们选择$L_2$损失函数来训练：$$L=\sum _{i,j}{l}_{ij},\text{ where }{l}_{ij}={\Vert u_j\left(t_{i+n},\cdot \right)-{\tilde{u}}_j\left(t_{i+n},\cdot \right)\Vert }_2^2$$这里$u_i\left(t_{i+n},\cdot \right)$是PDE-Net对于输入$u_i\left(t_i,\cdot \right)$所对应的输出。所有的PDE-Net中所涉及的滤波器都是有适当的约束通过使用与他们相关的矩矩阵。令$q_0$和$q_{ij}$为$D_0$和$D_{ij}$所对应的滤波器，我们使用一下的约束条件：$${\left(M\left(q_0\right)\right)}_{1.1}=1,{\left(M\left(q_{00}\right)\right)}_{1.1}=1|$$这里$i+j>0$。我们令${\left(M\left(q_{i,j}\right)\right)}_{k_1,k_2}=0,k_1+k_2\le i+j+2,\left(k_1,k_2\right)̸=(i+1,j+1)$;${\left(M\left(q_{i,j}\right)\right)}_{i+1,j+1}=1|$
为了展示可学习的滤波器的必要性，我们将会比较带约束的滤波器和冻结滤波器，我们把带有冻结滤波器的PDE-Net叫做“the Frozen-PDE-Net”。
NOVELTY OF THE PDE-NET:
使用可学习的过滤器使PDE网络更加灵活，能够对未知动态进行更稳健的近似，并能进行更长的时间预测。响应函数f的具体形式也是从数据中近似得出的，而不是假设的提前知道。通过对矩矩阵施加约束，我们可以确定微分运算符包含在基础PDE中，这有助于识别非线性响应函数f。这使得PDE网络和可能揭示隐藏的物理定律。

2.3. Initialization and training

在PDE-Net中，参数可以被分为三组：
1）用来近似微分算子的滤波器
2）用来近似F的神经网络的参数
3）超参数，如滤波器的个数、滤波器的大小、层数
其中，神经网络的参数在整个计算过程是共享的，由服从正态分布的数据做随机初始化。我们不直接训练n层PDE网络，而是采用分层训练，提高训练速度。所有参数在每个$\delta t-block$中是共享的。另外，我们第一个$\delta t-block$训练之前增加了一个热身的步骤。这个步骤是让近似F的神经网络获得一个好的参数初始化通过使用冻结滤波器。

2.4. Relations to some existing networks

• Network-In-Network(NIN)
• Deep Residual Neural Network(ResNet)

3. Numerical Studies: Convection-Diffusion Equations

3.1. Simulated data, training and testing

我们考虑一个2维的线性变参数对流扩散方程在$\Omega =[0,2\pi ]\times [0,2\pi ]$上$$\{\begin{array}{ll}\frac{\partial u}{\partial t}& =a(x,y)u_x+b(x,y)u_y+0.2u_{xx}+0.3u_{yy}\\ {u|}_{t=0}& =u_0(x,y)\end{array}(8)$$其中$(t,x,y)\in [0,0.3]\times \Omega$，且$\begin{array}{l}a(x,y)=0.5(\cos (y)+x(2\pi -x)\sin (x))+0.6\\ b(x,y)=2(\cos (y)+\sin (x))+0.8\end{array}$
数据通过高精度数值方法，通过将$\Omega$使用$50\ast 50$的网格离散，时间步长为$\delta t=0.015$求解（8）获得。我们假设边界条件和初值$u_0(x,y)$来自$$u_0(x,y)=\sum _{|k|,|l|\le N}{\lambda }_{k,l}\cos (kx+ly)+{\gamma }_{k,l}\sin (kx+ly),(9)$$其中$N=9$，${\lambda }_{k,l},{\gamma }_{k,l}\sim \mathrm{N}\left(0,\frac{1}{50}\right)$，$k$和$L$随机产生。同时我们也加入一些噪声数据：$$u(x,y,t)=u(x,y,t)+0.015\times MW(10)$$这里$M={\max }_{x,y,t}\{u(x,y,t)\},W\sim \mathcal{N}(0,1)$。假设我们知道了PDE是线性的且阶数不超过4，那么响应函数可以采用以下形式：
$$F=\sum _{0\le i+j\le 4}{f}_{ij}(x,y)\frac{{\partial }^{i+j}u}{\partial x^i\partial y^j}$$每一个PDE-Net中的$\delta t-block$可以写作：$$\tilde{u}\left(t_{n+1},\cdot \right)=D_{0}u\left(t_n,\cdot \right)+\delta t\cdot \left(c_{00}{D}_{00}u+c_{10}{D}_{10}u+\dots +c_{04}{D}_{04}u\right)$$这里$\left\{D_0,D_{ij}:i+j\le 4\right\}$是卷积算子且$\left\{c_{ij}:i+j\le 4\right\}$是一个用来近似函数$f_{ij}(x,y)$的二维矩阵。通过使用分段二次多项式插值，在每一块的边界处平滑过渡达到近似值。滤波器和卷积算子$\left\{D_0,D_{ij}:i+j\le 4\right\}$，同时分段二次型多项式系数是可训练的参数。
在训练和测试期间，数据是动态产生的，滤波器的大小使用$5\ast 5$或者$7\ast 7$。所有的可训练参数大约有17k。训练时，我们使用LBFGS而不是SGD去训练参数。我们使用28个样本/批次去训练每一层，我们只搭建PDE-Net到20层，一共需要560个样本/批次。

3.2. Results and Discussions

3.2.1. PREDICTING LONG-TIME DYNAMICS

我们首先展示训练好的PDE-Net在预测方面的能力。在有的pde-net训练完后，我们随机产生了560个基于（9）（10）的初始数据，将他们喂给PDE-NET，然后测量动态预测和实际动态变化之间的误差，将误差定义为：$$ϵ=\frac{\Vert \tilde{u}-u{\Vert }_2^2}{\Vert u-\overline{u}{\Vert }_2^2}$$其中，$u$是实际数据，$u$是预测数据，$\overline{u}$是$u$的平均值。
误差图如图3所示：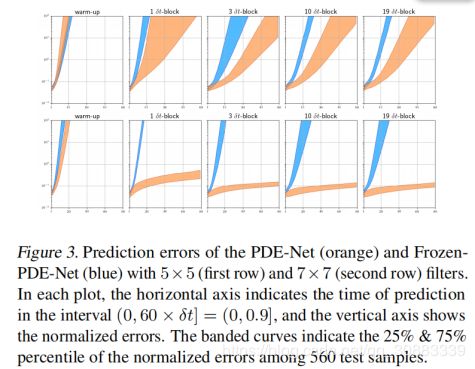
一些预测的动态变化的图片如图4所示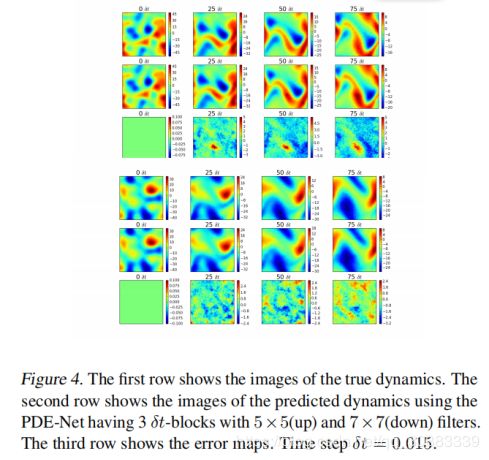
从这些结果中，我们可以看到：
1)即使在训练中加入了噪声数据，PDE-Net仍然可以实现长期的预测（见图4）
2)具有多个$\delta t-blocks$使得网络能够促进长期预测（见图3）
3)PDE网络的性能明显优于Frozen-PDE-Net，特别是对于7×7过滤器（见图3）,7×7过滤器的PDE网络在性能上明显优于5×5过滤器的PDE网络就可靠预测的长度而言（见图3）。达到一个O（1）误差，7×7滤波器的预测长度约为5×5滤波器的预测长度的10倍。

3.2.2. DISCOVERING THE HIDDEN EQUATION

对于线性问题，求解PDE相当于寻找近似$\left\{f_{ij}:1\le i+j\le 4\right\}$的系数$\left\{c_{ij}:1\le i+j\le 4\right\}$.已经训练好的PDE-Net的系数$\left\{c_{ij}:1\le i+j\le 2\right\}$如图5所示。注意$f_{11}{f}_{ij}:1\le i+j\le 2$不在PDE（8）中，以及由PDE网络得出的相应系数确实接近于零。

比较图5的第一个前三列，通过PDE-Net学习的系数$\left\{C_{ij}\right\}$与实际$\left\{f_{ij}\right\}$的系数非常接近。图5表明具有多个$\delta t-block$有助于系数的估计。然而使用较大的过滤器似乎不能提高系数的学习，尽管它对延长PDE网络的预测有很大帮助。

3.2.3. FURTHER EXPERIMEN

PDE（8）是二阶的，在我们前面的试验中，我们假设了PDE不超过4阶。如果我们知道PDE是二阶的，我们能够用更准确的方法估计对流和扩散项的变量系数。然而，预测的误差很高，因为我们只是用了较少的可训练参数。
为了能够更好的展示PDE-Net中滤波器的矩矩阵的重要性，我们训练了一个没有任何约束矩矩阵的网络。我们称这样的网络为 Freed-PDE-Net。Freed-PDE-Net.的预测误差如图6中的红色部分所示。因为没有力矩限制，不知道滤波器与微分器的对应关系操作。因此，我们无法识别对应的学习的变量系数。我们在图8中画出了15个变量系数。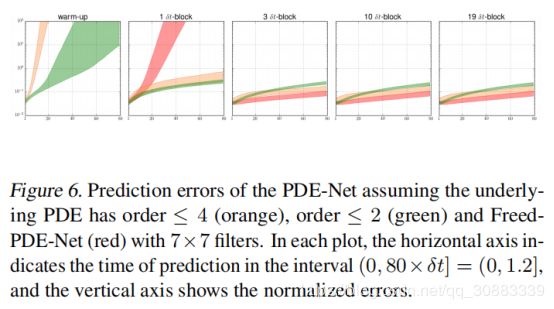


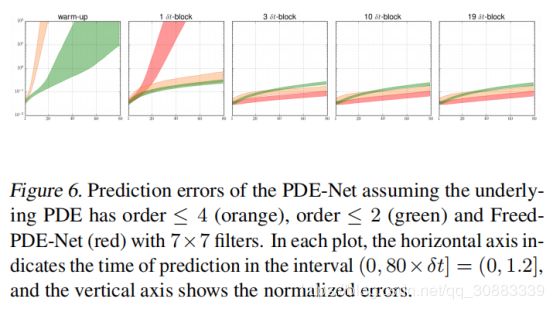
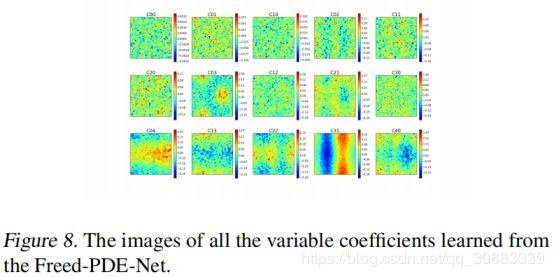
可以看出，Freed-PDE-Net的预测结果比PDE-Net要好，因为他有更多的可训练参数，然而，我们不能从Free-PDE-Net中识别出PDE。

4. Numerical Studies: Diffusion Equations with Nonlinear Source

4.1. Simulated data, training and testing

我们考虑这样一个2维带有非线性汇源项的线性对流方程：$\Omega =[0,2\pi ]\times [0,2\pi ]$$$\{\begin{array}{ll}\frac{\partial u}{\partial t}& =c\Delta u+f_s(u),\\ {u|}_{t=0}& =u_0(x,y),\end{array}\text{ with }(t,x,y)\in [0,0.2]\times \Omega (11)$$其中，$c=0.3$，$f_s(u)=15\sin (u)$，数据的产生与上个例子类似，时间步长改为$\delta t=0.0009$，同时有0边界条件。
我们假设响应函数$F$有如下形式：$$F=\sum _{1\le i+j\le 2}{f}_{ij}(x,y)\frac{{\partial }^{i+j}u}{\partial x^i\partial y^j}+f_s(u)$$PDE-Net中的每一个$\delta t-block$可以写作：$$\tilde{u}\left(t_{n+1},\cdot \right)=D_{0}u\left(t_n,\cdot \right)+\delta t\cdot \left(\sum _{1\le i+j\le 2}{c}_{ij}{D}_{ij}u+{\tilde{f}}_s(u)\right)$$其中$\left\{D_0,D_{ij}:1\le i+j\le 2\right\}$是卷积算子,$\left\{c_{ij}:1\le i+j\le 2\right\}$是$f_{ij}(x,y)$的近似，是一个二维矩阵。在我们的试验中，滤波器的大小为7*7，参数量大约为1.2k。

4.2. Results and Discussions

4.2.1. PREDICTING LONG-TIME DYNAMICS

我们首先展示训练好的PDE-Net的预测能力。
图9是PDE-Net和Frozen-PDE-Net的对比；
图10是动态预测的可视化结果；
所有的这些结果表示，PDE-Net在预测方面表现很好

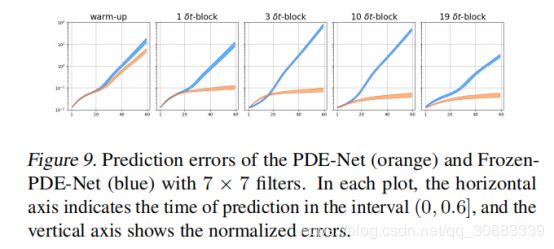
4.2.2. DISCOVERING THE HIDDEN EQUATION

对于PDE（11），确定PDE相当于寻找近似$\left\{f_{ij}:1\le i+j\le 2\right\}\}$的系数$\left\{c_{ij}:1\le i+j\le 2\right\}$和$f_s$的近似$f_s$。
经过训练的PDE网的计算系数$\left\{c_{ij}:1\le i+j\le 2\right\}$如图11所示，计算出的如图12（左）所示。注意到一阶项不在PDE（11）中以及PDE-Net学习到的相应系数实际上接近于零。$f_s$的近似值在区间中心附近比在边界附近更精确。这是因为数据集中的u值主要分布在中心附近（图12（右））。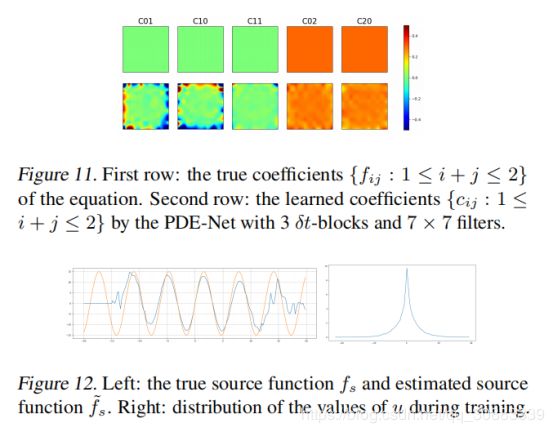

5.Conclusion and Discussion

在这篇文章中，我们设计了一个深层的前馈网络叫PDE-Net，为了从观测到的动态变化中发现隐藏的PDE模型并预测其动态行为。
PDE-Net参与训练的主要由两部分组成：
1)通过合适的带约束的滤波器做卷积来近似微分算子
2)通过深层神经网络来近似非线性响应函数
这个PDE-Net适用于学习PDE（1）类型。以线性变系数对流扩散方程为例。结果表明，PDE网络能够揭示观测动力学的隐式方程，并能在较长的时间内，甚至在噪声环境中预测动态行为。其中一个重要的方向是揭示传感器无法直接测量的隐藏变量，如数据同化。另一个值得探索的方向是学习基于PDE网络结构的给定PDE模型的稳定一致的数值格式。