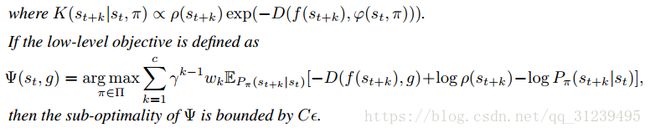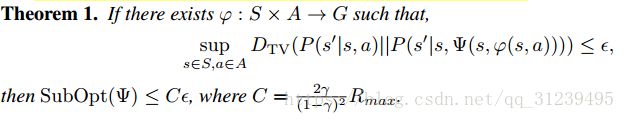NORL(near-optimal representation learning for hierarchical reinforcement learning)

论文：https://arxiv.org/pdf/1810.01257.pdf

摘要：

论文研究有目标导向的层次化的强化学习表示。在层次化结构中，高层控制器通过反复沟通（确认）目标，该目标由低层策略训练得到。同时，表示的选择，即目标区域到探索区域的映射是至关重要的。为了研究这个问题，论文提出表示学习sub-optimality(低层最佳性)的概念，由使用该表示的优化策略的期望奖励定义。论文提出表达式结合 sub-optimality，展示该表达式可以转化表示学习目标。论文提出的算法在许多连续控制任务中表现优异，且明显优于其他算法。

介绍：

goal-conditioned层级设计中，高层策略与低层策略的目标沟通，低层策略根据达到的状态得到奖励。在多层设计中，表示学习映射探索空间和目标空间。

论文学习非监督目标用于训练表示，该表示更简洁，并且相对于端对端(end to end)具有更强的解释性。表示学习中一个重要的问题是：使用一个表示信息，该表示相对于完全表示，有多少信息因为期望奖励和最优策略丢失？该问题阐述了有用的表示学习如何压缩状态，使得学习问题更加简单。

论文的理论提出：对于一个特定选择的表示学习目标，可以通过返回的层级策略与返回的最优策略的边界误差来学习表示学习，然后论文提出优化该边界的方法。论文表明：表示学习的层级化目标设定策略和实时抽象提取可以在最优策略下达到次最佳。

框架：

论文提出一个基于MDP(马尔科夫决策链)的两层策略，高层策略通过选择目标状态和低层策略达到该状态的奖励来调节低层策略的行动。高层策略：，其中表示目标空间，每c步选择的目标。低层策略是基于目标的，，将高层的动作转化到低层动作中，其中，。

每隔c步，选择一个状态，使用高层策略采样一个目标，并转化为策略，使用策略采样动作。

其中，的公式可以定义如下：

      

次最佳层级化策略：

论文提出两个问题：① 高层策略只能通过策略以MDP方式学习，该学习过程会丢失多少信息？② 即使存在中的潜在损失，是否仍然可以学习一个层级化策略可以接近最优？

解决上述两个问题，论文提出了次最佳的概念，作为基于目标G的最佳高层策略，作为目标G与低层动作之间的映射。作为基于MDP的全层级策略，将比作映射未知的最优层级策略。引入的未知最优高层策略，表示在每隔c步，该策略采样低层的动作，使用这种方法，可以采样到所有可能的低层动作，然后定义作为的全层级策略。

论文引入映射的次最佳策略：其中，表示策略π在状态s中未来的值，由映射决定，同时反过来决定表示的选择。在这里次最优和表示f之间的关系还不清楚，论文后续会分解这些项。

好的表示导致次最佳边界：

对于条件目标策略和表示学习的次最佳，论文在声明4中阐述，该声明是论文最主要的结论，声明如下：

要理解声明4，需要从一些定理开始推导，定理1如下：

定理1中，高层策略在中通过映射选择一个行为，论文量化在不同的目标g下，通过产生的所有低层策略可能的行为。为了量化该目标，论文使用了可逆的目标模型，用于预测在目标g下通过产生的行为，该模型会引入一个近似于分布的分布，然后计算两个分布之间的散度。

定理1假设了所有行为的影响都是可恢复的，可补偿的。在任意的状态空座空间，存在目标空间g，g能引出相似的下一状态分布。论文进一步提出了声明2，如下所示：

声明2中是由表示f和状态目标映射所决定的一个动态模型，通过界定动态分布和之间的差异，上述公式（4）表明表示 f 应该在基于的动态表示空间中被选择，其中决定了目标空间g。

如果低层的强化学习目标像公式（5）那样，那么最小化次最佳性时只需要优化一个基于公式（4）的表示学习目标。

论文提出定理3，如下所示：

其中，表示低层动作策略，表示高层动作，该动作在每 c 步执行，且通过 c 步转化为低层动作策略，即，可逆目标模型是一个映射，从到 G ，用于预测使得引起策略的目标g，其中引入特征状态分布，在时近似于分布。

论文在权重，，最终。

最后回到上述提到的声明4，也就是论文最重要的部分，最小化次最佳性就可以直接通过优化表示学习目标来达到。

学习：

其中，是公式（8）的内部分解表达式，B是常数。

论文在学习一个底层的策略时，公式如下:

实验结果：

 

思考：

① 引入定理1的意义是什么？为什么要提出该定理？

由于高层空间确定的目标G空间很难确定，若要使得该goal空间成为一个与目标（即任务相关）的空间，可以采用次最佳的思路，使用另外一个分布来近似逼近原目标空间的分布，从而达到确定G空间的目的。因为不是直接求解G空间，那么使用KL散度，来度量假设的分布与真实分布之间的距离是最合适不过的。该定理的作用是避开直接求解很难求解的问题，而通过近似逼近的方法来得到目标空间。

 

② 论文提到的公式（1）的物理意义是什么？

公式（1）表示的是目标与状态的映射关系，其中D表示一个距离方程，用来度量（奖励）低层策略，表示在策略π下，从k步开始到t+k步的状态的分布。该公式物理显示出，选择不同的表示，将会影响到目标与状态之间的映射关系。

 

③函数物理意义是什么？

首先我们需要知道函数是什么，论文中提到，函数是为了将公式（8）在实际操作中可训练而进行的转化，公式（8）如下：

y是衰减函数，可以从贝尔曼公式的理论解释。表示在策略π下，从k步开始到t+k步的状态的分布；表示 f 和状态目标映射所决定的一个动态模型，通过界定动态分布和之间的差异，其中表示 f 由得到。

 

④ 论文的数据流向？

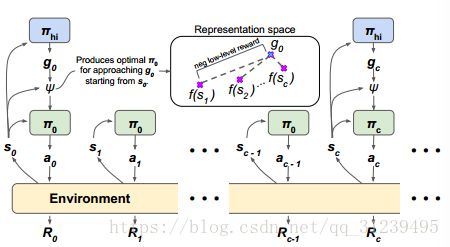
论文中有一张数据流向图，如下所示：环境将状态传递给高层策略，动态函数是由高层策略确定的目标g而确定的，用于给低层策略选定目标，低层策略πo则由MDP决策过程与环境进行互动，不断迭代直到策略达到最优（次最佳性）。

 

⑤ 论文的层次化结构的优点在哪儿？有什么优势？

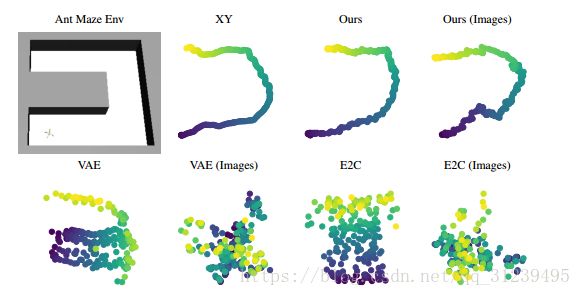
论文的层次化结构使得算法可以以任务为导向，传统的VAE，GAN等算法都与任务无关，而使用层次化的结构使得生成模型可以以任务为导向，进行更加有效率有目的的生成表示，给有任务的生成学习提供了一个好的研究方向。

 

备注：思考中可能有错误的地方，不全面的地方，欢迎指正。