[算法] 从简入深理解动态规划
动态规划(dynamic programming)
本文总结于UCAS的卜东波老师的计算机算法设计与分析课程中的动态规划一讲
文章目录
- 动态规划(dynamic programming)
- 矩阵链乘问题
- 问题描述
- 基本分析思路
- 伪代码(第一版)
- 时间复杂度分析
- 优化时间复杂度方案
- 伪代码(第二版)
- 回溯求解最优解计算顺序
- 伪代码(第三版)
- 动态规划总结
- 额外解法(复杂度O(nlogn) )
在说动态规划之前先看一下它和分治之间的 区别:
-
分治算法是把原问题分解为若干个子问题(子问题是相互独立的)。自顶向下求解子问题,合并子问题的解,从而得到原问题的解。
-
动态规划也是把原始问题分解为若干个子问题(一般子问题有联系,子问题有重叠部分),一般自底向上进行求解,先求解最小的最优子问题,把结果存在表格中(通过记录表从而避免计算重叠的子问题),在求解大的最优子问题时,直接从表格中查询小的最优子问题的解,避免重复计算,从而提高算法效率
那么一般在什么情况下使用动态规划呢?
如果一个问题求解过程可以看成多步决策的问题,那么就基本可以使用动态规划来求解该问题。
下面以一个矩阵链乘问题的实例来分析如何使用动态规划求解问题的。
矩阵链乘问题
问题描述
INPUT: A sequence of n matrices A1, A2, …, An; matrix Ai has dimension pi−1 × pi ;
OUTPUT: Fully parenthesizing the product A1A2…An in a way to minimize the number of scalar multiplications.
该问题是找到矩阵链乘过程中最小标量相乘的个数。
因为矩阵相乘的先后顺序会改变标量相乘的个数。如下面这个例子:
![[算法] 从简入深理解动态规划_第1张图片](http://img.e-com-net.com/image/info8/7328d61633694f3894f23ef279895c64.jpg)
基本分析思路
将问题描述为加括号的多步决策(每次加一对括号),如第一次在k那个元素进行划分为
(A1...Ak)(Ak+1...An).
这样就把原问题分成两个独立的子问题:
计算A1…Ak的最优加括号策略和计算Ak+1…An的最优加括号策略
这里分别用Opt(1,k) 和Opt(k+1,n)表示两个子问题的最优解。
通过组合子问题的最优解,可以得到原问题的最优解。这可以用递归表达式写出以下等式:
O P T ( 1 , n ) = O P T ( 1 , k ) + O P T ( k + 1 , n ) + p 0 p k p n OP T(1, n) = OP T(1, k) + OP T(k + 1, n) + p0pkpn OPT(1,n)=OPT(1,k)+OPT(k+1,n)+p0pkpn
目前我们面临的问题是,仍不知道最优解第一次分裂的位置k,一个显而易见的解决方案就是枚举,列 举所有的可能,即 k= 1,2, 3,…,n-1。这样我们就能够得出以下递归: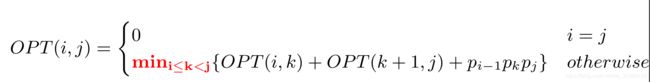
伪代码(第一版)
RECURSIVE_MATRIX_CHAIN(i, j)
1: if i == j then
2: return 0;
3: end if
4: OP T(i, j) = +∞;
5: for k = i to j − 1 do
6: q = RECURSIVE_MATRIX_CHAIN(i, k)
7: + RECURSIVE_MATRIX_CHAIN(k + 1, j)
8: +pi−1pkpj ;
9: if q < OPT(i, j) then
10: OPT(i, j) = q;
11: end if
12: end for
13: return OPT(i, j);
时间复杂度分析
先看一下菲波那切数列(指数级时间复杂度):
f ( n ) = f ( n − 1 ) + f ( n − 2 ) f(n) = f(n-1) + f(n-2) f(n)=f(n−1)+f(n−2)
if n = 0 f(n) = 0
if n = 1 f(n) = 1
因为子问题重复的计算了(重叠子问题),所以很慢
对于多个矩阵相乘这个问题的时间复杂度也是类似,重复计算了子问题,可以证明这是一个指数级的时间复杂度问题。
优化时间复杂度方案
算过的子问题都存下来(开一个数组存储),每次运算的时候判断是否计算过子问题,用空间换时间!
粗略估计改变后的时间复杂度:
子 问 题 个 数 x 每 个 子 问 题 花 费 的 时 间 子问题个数x每个子问题花费的时间 子问题个数x每个子问题花费的时间
解释:这里有n2的子问题,每个子问题需要循环一次,所以仅是O(n3),对比之前的指数级的时间复杂度(之前是指数个可能)。
*为什么用DP快?*因为每次计算都基于前一步的最优解上进行。
伪代码(第二版)
MEMORIZE_MATRIX_CHAIN(i, j)
1: if OPT[i, j] ̸= NULL then
2: return OPT(i, j);
3: end if
4: if i == j then
5: OPT[i, j] = 0;
6: else
7: for k = i to j − 1 do
8: q = MEMORIZE_MATRIX_CHAIN(i, k)
9: +MEMORIZE_MATRIX_CHAIN(k + 1, j)
10: +pi−1pkpj ;
11: if q < OPT[i, j] then
12: OPT[i, j] = q;
13: end if
14: end for
15: end if
16: return OPT[i, j];
可以看到这一版本的代码仅仅在上一个版本的代码多了三行。
回溯求解最优解计算顺序
在上面两版代码中都能够解决这个问题,并且给出最优解,那么我们如何得到最优解的计算顺序呢?
**回溯 !**从OPT(1,n)开始,我们追溯到OPT(1,n)的来源
具体操作:
使用辅助数组 S[1…n, 1…n] ,S[i,j]记录了最优决策,即k的值,
ps:若有 A1A2A3A4矩阵相乘,S[1,4] = 3则表示加括号的方式为(A1A2A3)(A4)
伪代码(第三版)
在这个版本中将递归函数拆分出来,写成循环结构,并使用辅助数组S记录k值
MATRIX_CHAIN_MULTIPLICATION(p0, p1, ..., pn)
1: for i = 1 to n do
2: OPT(i, i) = 0;
3: end for
4: for l = 2 to n do // l 表示子问题中有几个矩阵进行链乘,当l=2时是确定的子问题,可以直接求解出来
5: for i = 1 to n − l + 1 do
6: j = i + l − 1;
7: OPT(i, j) = +∞;
8: for k = i to j − 1 do
9: q = OPT(i, k) + OP T(k + 1, j) + pi−1pkpj ;
10: if q < OPT(i, j) then
11: OPT(i, j) = q;
12: S(i, j) = k; //记录最优值的k
13: end if
14: end for
15: end for
16: end for
17: return OPT(1, n);
动态规划总结
- 首先把求解问题描述成多步决策过程
- 确定目标函数可分
- 通过总结所有可能的子问题形式,定义子问题的一般形式(根据具体的例子)
- 证明了子问题之间的地推可以表示为最优子结构性质,即问题的最优解包含子问题的最优解
- 如果递归算法一次又一次的解决同一子问题,则可以使用“表格”来避免重复解决相同的子问题。
额外解法(复杂度O(nlogn) )
类比于多边形三角剖分算法
这里先留白,