基于神经网络的目标检测论文之神经网络基础:梯度下降和误差反向传播算法
注:本文源自本人的硕士毕业论文,未经许可,严禁转载!
原文请参考知网:知网地址
本章节有很多公式没有显示出来,去看本人原版论文吧。
第二章 深度神经网络的理论基础
2.1 神经网络的结构
2.1.1 人工神经元模型
神经网络的设计是类比人类大脑进行设计的,神经生物学家将人工神经网络视为一种解释神经生物现象的研究方法。人类大脑通过对数以亿计的神经元进行合理组合,能够产生比计算机快好几个数量级的运算速度。
神经元作为构成人工神经网络结构中的最小单位,也是后续章节中设计人工神经网络的基础,图2-1给出了人工神经元的模型。

图2-1 人工神经元示意图
图2-1中为我们展示了一个标准神经元的三种基本组成单元:
1,连接:每一个连接都连接到求和节点,每一个连接都有一个权重。由图2-1所示,第j个连接上的信号 乘以连接权重 作为该连接上的输入值。人工神经元的权值取值固定在一个范围内,作为待学习的参数。
2,加法器:加法器上的主要是将所有连接传递过来的输入值做累加和操作。结果作为激活函数的输入值。
3,激活函数:激活函数接收加法器的输出值,并将输出值做非线性变换并将输出结果压缩到小范围。通常,单个神经元的输出范围为单位闭区间。
图2-1中的神经元还应该加上外部偏置量(bias),记为 。偏置同样作为一个待学习的参数,适当提高或减小激活函数的输入值。
一般用下面一组方程来描述神经元:
(2-1)
(2-2)
其中 , , , , 是输入单元, , , , 是神经元各连接的权值, 是加法器的输出, 为偏置,激活函数为 , 是输出。
2.1.2 激励函数的类型
激励函数(activation function),也叫激活函数,主要作用是用来对输入值做变换,变换到一个固定的区间。激励函数用于 函数之后,用来加入一些非线性的因素。下面我们给出三种常见的激励函数:
1、阈值函数。函数图像如图2-2(a)所示,将输入值映射成为两个固定的值。可惜的是阈值函数不连续,在实际中并不常用。
2、Sigmoid函数。函数图像如图2-2(b)所示,该函数的图像平滑且连续,经常用于构建人工神经网络。函数的定义如下式2-3所示,其中a是Sigmoid函数的倾斜参数。
(2-3)
3、ReLU函数。函数图像如图2-2(c)所示,ReLU函数(rectified linear units)是目前大部分卷积神经网络CNN(convolutional neural networks)中常用的激励函数,该函数的形式是 ,在该函数的原点左侧部分斜率是0,在原点右侧则是一条斜率为1的直线。从函数图像看出,这显然是非线性的函数, 小于0时输出为0, 大于0时输出就是输入值。
三个激活函数的函数图像如图2-2所示:
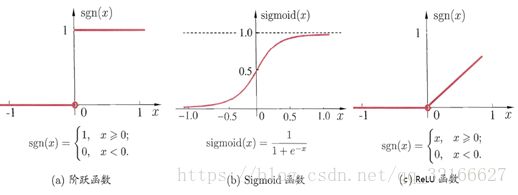
图2-2 三种激活函数的图形
2.1.3 前馈网络结构
深度前馈网络(deep feedforward network),也称为多层感知机(multilayer perceptron,MLP)或者前馈神经网络(feedforward neural network),是目前典型的深度学习模型。这种模型之所以被称为前馈的,是因为网络中信息从原始输入开始,流动方向经过输入层神经元,中间经过隐藏层,到达输出层神经元。在模型本身和模型的输出之间没有反馈(feedback)连接。
构建网络的目的就是为了拟合出某个函数 ,使得其无限接近于实际输出。拿分类器举例子,函数 接收输入 ,输出预测的类别 ,于是网络就可以定义一个映射 ,通过拟合训练样本进而学习参数 的值,得到最优的拟合度。前馈网络对于学习机器学习和深度学习是极其重要的,它在很多重要的领域中扮演重要角色。例如:对图像中的物体进行识别的卷积神经网络就是一种专用的神经网络,前馈网络也是循环神经网络的基石,循环神经网络在语音和自然语言处理应用中占统治地位。
前馈网络这种模型的拓扑结构是一个有向无环图,并且这个有向无环图描述了函数是如何复合在一起的。例如:我们有三个函数 、 和 连接在一个链上以形成 。这种链式结构是神经网络中最常用的结构。在这种结构中, 称为的第一层(first layer), 称为第二层(second layer)。拓扑结构的深度称为模型的深度(depth)。网络拓扑结构的最后一层被称为输出层(output layer)。在训练的过程中,每一轮迭代都让 去匹配 的值。训练数据中每个样本都有一个标签 。
这些网络被称为神经网络是因为它们早起的发明是受神经生物科学的启发。网络中包含多个隐藏层,这些隐藏层的神经元个数决定了模型的宽度。向量的每个元素都类似于一个神经元的作用。我们可以把层看成由许多并行操作的单元组成,每个单元在某种意义上类似一个神经元,结构如图2-1所示。
用于计算这些表示的函数 的选择也受到神经科学的启示。事实上,现代的神经网络研究理论更多来自数学和实践的指引,并且人工神经网络并不能完美地给大脑建模。不要将神经网络看成是对人脑的模拟,看作是为了实现近似模型的算法。它从大脑中运行机制获取灵感,但并不能模拟大脑功能。
沿用单隐藏层前馈网络的分析,当隐藏层个数超过2层时,成为多层前馈神经网络,其网络的拓扑结构特点是:多隐层、全连接、有向且无环。多层网络结构如图2-3所示:

图2-3 四层神经网络结构
2.1.4 梯度下降算法
接下来需要计算权重和偏置,以使得输出y(x)拟合输入x。首先利用方差的概念定义一个代价函数(2-4):
(2-4)
公式(2-4)在总体训练样本 上计算平均误差。一般函数C 称为二次代价函数,也称为均方误差。
由公式(2-4)可以看到C( ,b) 是非负的。可以明显的看到,当给定所有的训练样本x,y(x)接近于输出a 时,代价函数C( ,b)的值相当小,即C( ,b) ≈ 0。这给算法的工作以很大的启示,如果算法能找到恰当的权重和偏置,能够使得C( ,b) ≈ 0,就可以说算法学习到了知识。反之,则差别很大。因此算法的目的是最小化代价函数C( ,b),即找到能让代价函数尽可能小的权重和偏置。梯度下降算法在是常用的计算梯度的方法,用它来达到最小化误差的目的。梯度下降如图2-4所示:
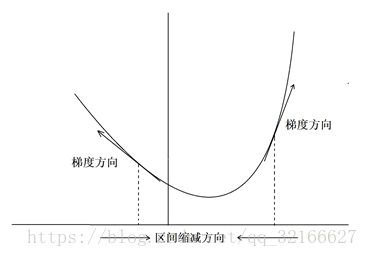
图2-4 梯度下降示意图
为了最小化C,想象C 是只有一个变量的函数。一元函数很容易找到全局最小值,实际中函数C是一个极其复杂的多元函数,要借助于计算工具求最值。
最先想到的解决方案是用求偏导数来计算最小值,可以计算函数中每一个变量的偏导数最终计算C 的极值。神经网络中一般有数以千万级的变量。用微积分来计算最小值将使得计算量暴增。
那么还有什么方法能找到最小值呢?利用微积分的定义式,在两个变量v1 和v2上加一个小的增量Δv1 和Δv2时,微积分的定义公式(2-5)告诉我们函数C 将会有如下变化:
(2-5)
为了让误差函数变小,算法要寻找一种选择增量的方法使得ΔC为负。为了方便接下来的推导公式,定义Δv是v的变化向量, 。
与此同时还定义C的梯度向量形式: ,用符号 来表示偏导数向量,即:
(2-6)
定义好以上表达式后,ΔC可以被重写为:
(2-7)
表达式(2-7)解释了用 表示梯度向量的好处: 清晰地将v的变化转化为C的变化。注意,表达式(2-7)写成这样的目的是决定怎样选择Δv才能让ΔC负增长。假设我们选取:
(2-8)
公式(2-8)中的 称为学习速率,它是个很小的正数。方程(2-7)告诉我们 。由于 ,这保证了 。根据方程(2-8)的形式重复计算并改变梯度,最终达到极小值。方程(2-7)用于定义函数的变化规律。方程(2-8) 用来计算Δv,并修改v的值,如公式(2-9)所示:
(2-9)
梯度下降就是一直重复计算梯度 ,最终得到损失函数的最小值。因此,梯度下降法可以被视为一种在C下降最快的方向上做微小变化的方法。
最后补充一点,梯度下降工作时应该使用小的学习速率 使得损失函数可以稳步接近极小值。否则,函数会在极小值附近徘徊,并最终停在极小值附近。然而 不能任意小,这会使算法运行得缓慢,学习不到知识。在实际使用中, 通常是变化的,算法开始训练时每次变化较大,接近极值点时再将训练速度放慢,最终稳定在极值点结束。
2.1.5 误差反向传播算法
本节介绍快速计算梯度的算法,也就是反向传播(backpropagation)[37],即怎样计算损失函数的梯度。反向传播是损失函数C 对w(或者b)偏导数 的表达式。
首先给出权重的定义,用 定义 层 个神经元到 层 个神经元的连接上的权重。例如, 就表示网络中两个神经元的连接上的权重。同样地, 定义 层第 个神经元的偏置, 定义 层上第 个神经元的激活值。于是 层的第 个神经元的激活值 就和 层的激活值关联起来:
(2-10)
其中求和是在 层的所有k个神经元上进行的。我们对每一层l都定义一个权重矩阵 ,是为了用矩阵的形式重写这个表达式,即把公式向量化。权重矩阵 的元素正是连接到 层神经元的权重,类似的,对每一层l,定义一个偏置向量 。最后引⼊向量化函数 按照矩阵形式重写公式(2-10)。公式(2-10)被写成下面这种简洁的向量形式:
(2-11)
公式(2-11)简化了层与层之间的连接方式。权重矩阵乘以激活值加上偏置向量,最后传递给 函数。l层神经元的带权输入是中间量 。向量表示法更加简明。
反向传播研究的是梯度变化如何影响代价函数的过程。为了计算偏导数 和 ,引入变量 ,其表示在第 层上第 个神经元上的误差。
接下来使用公式推导反向传播的过程。这些公式提供一种计算误差 和梯度的方法。
1、output层的误差公式:
BP1a)
公式(BP1a)对 来说是针对单个神经元的写法。矩阵表示的形式有利于运算并且书写方便。所以以矩阵形式重写公式,其中 运算称为Hadamard乘积,按照向量的元素进行乘积:
(BP1b)
2、使用下一层的误差 来表示当前层的误差 :
(BP2)
现在我们知道了前一层 的误差 。公式(BP2)是前一层误差关于后一层误差的函数,可以看作是误差在沿着网络反向传播。由公式(BP1)和(BP2)联合使用,可以计算出任一层的误差 。重复计算便反向传播完整个网络。
3、偏置的改变率:
(BP3)
公式(BP3)计算梯度,误差 和梯度 完全一致。前两个公式已经给出计算 的方法。
4,权重的改变率:
(BP4)
同上计算梯度 ,公式中用到的 和 这些量已经知道如何计算了。算法从最后一层开始向前计算误差向量 ,也是被称作反向传播的原因。具体计算流程如下:
1、输入训练样本:激活值 向后传播。
2、激活值前向传播:计算每一层的 。
3、输出层产生误差:计算向量 。
4、误差反向传播:计算每一层的 。
5、调整权重:梯度由 和 得到。