深度学习框架Keras学习系列（二）：神经网络与BP算法（Neural Network and BP Algorithm）

概念

神经网络

请参照这篇文章神经网络浅讲：从神经元到深度学习，以对神经网络的发展历史以及其数学原理有一个基本的了解。本文只对将要在后续过程中使用的神经网络模型进行介绍。

神经网络本质上是一个数理模型，它最初的灵感来自于人大脑中的神经系统，不过发展到后来已经与其灵感来源没什么太大关联了。

要了解全局，我们首先要了解局部。

神经网络（artificial neural network）本质上就是由多层（layer）神经元（neuron）构成的一个可接受输入，并能输出结果的一个算法（algorithm）。

既然神经网络的基本单位是神经元，那么我们就首先来看，神经元的定义是什么。而神经元的定义，我们参考Andrew Ng在Deep Learning教程中的引入方法来介绍，从Logistic Regression说起。

Logistic Regression

给定一个样本的x（特征输入向量），我们想得到该样本所属的类别y（0或1）。不过我们希望有个模型最好能告诉我们，该样本属于1或0的概率是多少，于是，logistic regression应运而生。

用公式来表达：

Given x, want ŷ =P(y=1|x) , x∈Rnx

Parameters: w∈Rnx , b ∈ R

Output: ŷ =σ(wTx+b)

z:=wTx+b

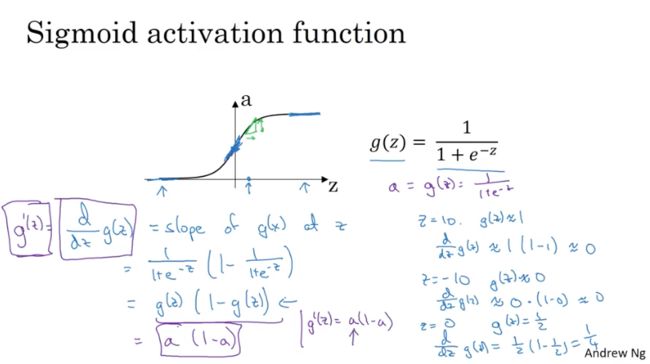
另外，我们将z代入一种名为sigmoid的函数，看函数的值如何随z的变化而变化。

可以看出，sigmoid函数的特性是，当z很大，函数值接近1，z很小，函数值接近0。而这个输出的值域刚好和概率值的值域是一致的，因此，我们可以将一个训练好的logistic模型输出的值作为判断一个样本属于某个类的概率。

而最终，我们的logistic regression模型的目标就是学习最好的w和b参数，以使得模型能够在判断新样本的类型时，有最高的正确率。

获得最优w，b参数的过程叫做训练，训练需要首先找到一个成本函数（cost function），作为模型是否被训练的足够好的参考。

在线性模型的训练中，损失函数（Loss（error） Function）被定义为：

l(ŷ ,y)=12(ŷ −y)2

，但是logistic regression的模型不能采用这个损失函数，因为该函数会在这里编程非凸（not convex）函数，导致训练很容易陷入一个局部最优解（local optima），即梯度下降无法获得好的效果，导致最终不能得到足够好的模型。

（注意，损失函数针对的是在单个样本上的误差，而成本函数针对的是整个训练集的平均误差，成本函数是最终的优化目标【参考这里】）

于是，针对这种情况，LR采取了以下特定损失函数：

l(ŷ ,y)=−(ylogŷ +(1−y)log(1−ŷ ))

这个损失函数的特性是：
- 当y=1， l(ŷ ,y)=−logŷ  , 而此时若 ŷ  的值偏离1比较远（由于sigmoid函数的取值，只能是向0方向偏移），根据log函数的特性， l(ŷ ,y) 会变得特别大。
- 当y=0， l(ŷ ,y)=−log(1−ŷ ) , 而此时若 ŷ  的值偏离0比较远（由于sigmoid函数的取值，只能是向1方向偏移），根据log函数的特性， l(ŷ ,y) 会变得特别大。

这样就造成了，一旦LR模型在预测某个样本出错，即输出值与真实值差别比较大时，损失函数都会输出非常大的损失值，使得算法在训练过程中对参数进行较大程度的调整，以达到有效调整模型表现的效果。

梯度下降算法（Gradient Descent）

现在，针对LR模型，我们有了训练的目标参考，即成本函数J(w,b)。

ŷ =σ(wTx+b),σ(z)=11+e−z

J(w,b)=1mΣmi=1l(ŷ (i),y(i))=−1mΣmi=1y(i)logŷ (i)+(1−y(i))log(1−ŷ (i))

成本函数所代表的含义：在有m个训练样本的训练集上，当前算法给出的模型对所有样本的损失函数的加总平均。

而我们判断模型是否学得好的标准就是，成本函数的值是否已经达到最小。而我们的目标就是，找到w,b使得J(w,b)可以达到最小值。

理论已经证明，LR模型的成本函数是一个凸函数，即只有一个最小值点，于是我们可以用梯度下降GD完成寻找最小值点的任务，最终获得我们所需要的参数w,b的值。

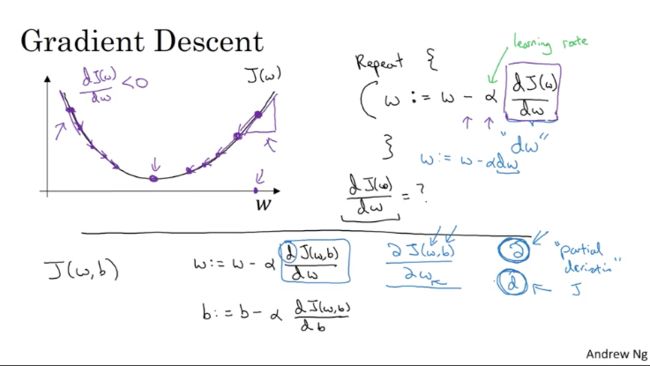
• GD的做法

GD的做法本质上来说就是：通过函数对目标参数值求偏导，获得目标参数值点在当前位置的梯度（gradient），然后让目标参数在梯度的负方向上进行值的更新，以使得函数的值更小。而之所以要再梯度方向上进行移动，是因为这样可以使函数值减小的最快。（可以用泰勒公式证明：函数的某个变量向其负梯度的方向移动，函数值会减小）

---

泰勒公式证明梯度下降的有效性：

泰勒公式本质就是用多项式函数去逼近光滑函数。之所以要用多项式函数去逼近，是因为光滑的函数本身可能无法算值，而多项式是可以求值的。

根据泰勒公式，在包含 x0 的区间上，某函数f(x)若在 x0 处n+1次可导，那么对于这个区间上的任意x都有：

f(x)=f(x0)+f′(x0)!1(x−x0)+f″(x0)!2(x−x0)2+...+f(n)(x0)!n(x−x0)n+Rn(x)

当 x0=0 时，就是泰勒公式的特例——麦克劳林公式。

由于 f(x0) 二阶以上的导数项的值都接近于0，可以忽略不计，所以我们干脆去掉 f″(x0)!2(x−x0)2 及之后的所有项，只剩下：

f(x)=f(x0)+f′(x0)!1(x−x0)

由于 f(x0) 的值固定，于是，为了让f(x)的值变小，我们需要做的是让 f′(x0)!1(x−x0) 为负数，且尽可能小。此处， f′(x0) 即为f(x)在 x0 处的梯度，如果它为正，就需要后面的 (x−x0) 为负数；如果它为负，就需要后面的 (x−x0) 为正数，即 (x−x0) 的值永远应该和梯度的值异号（梯度的负向）。

---

在这里，我们的目标参数值是w和b，因此需要使用成本函数对w和b分别求偏导，然后在每次进行梯度下降的过程中，同时更新w和b的值，即重复：

w:=w−αdJ(w,b)dwb:=b−αdJ(w,b)db

这里的 α 是一个称为学习速率（learning rate）的参数，它的取值范围是(0,1]，它决定了梯度下降的幅度/速度。

Logistic Regression的梯度下降

学习完GD后，我们利用GD的思想，对LR模型的成本函数进行优化/参数更新，优化的过程需要用到偏导的计算，而偏导的计算又会涉及到链式法则。

对于单个样本的参数更新过程如下：

对于整个训练集，即m个样本的优化过程：

神经网络模型

前面铺垫了那么久讲logistic回归，其实主要就是因为，神经网络本身就可以看做由很多个logistic回归模型组合而成。

如下图：上面是一个典型的LR模型，而下面就是一个简单的神经网络（Neural Network，简称NN）。你会发现，NN其实就是让原来相同的输入向量现在不只对一个点进行输出，而是同时对多个点进行输出，并且接受输出的点还可以成为新的输入源，继续向后输出，并不断嵌套。（LR则直接经过sigmoid函数一层转化后输出结果了）

NN的表示

如图是一个两层（NN的层数不包含输入层，因为输入层并不是一层神经元）的NN：

概念：

• 输入层（Input Layer）：输入到NN的原始特征向量。
• 隐藏层（Hidden Layer）：处理中间数据的层。
• 输出层（Output Layer）：输出结果的层。

符号：

• a[i]j ：第i层的第j个神经元的输出（之所以用a表示，是因为除开输入层，其它层的任一神经元输出都是对输入的值用激活函数（Activation Function）处理后的值），而 a[0] 指的就是输入层的原始值
• X：输入特征向量
• ŷ  ：模型的输出
• W[i] ：第i层的权重矩阵
• b[i] ：第i层的截距项

计算NN的输出

承接上一部分的二层NN继续讲解。

首先，我们集中视野到单个神经元上：

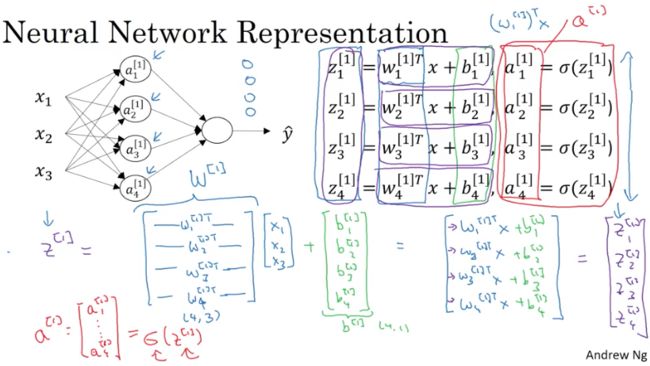
我们针对隐藏层的神经元，逐个计算它们的输出。

为了让计算简便（不用for循环逐个计算各个隐藏层神经元的z值），我们将权重矩阵 W[1] 直接和输入向量x相乘，并加上截距项向量b，直接获得z向量（vectorization）。

最后，对z值向量进行elementwise的sigmoid函数处理，即获得了隐藏层的输出向量 a[1] 。

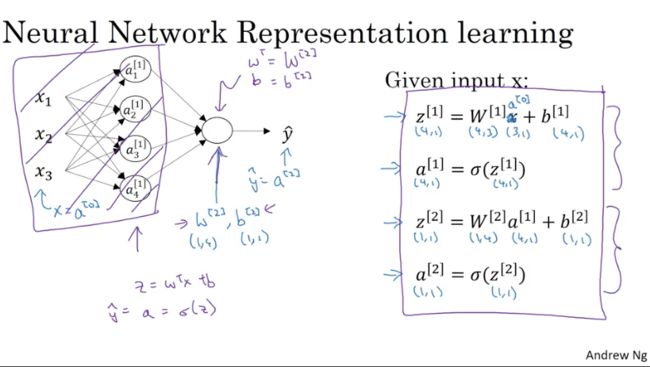
如下图，总结一下：对于一个只有一层隐藏层的NN，给定一个输入x，我们进行以下四步就可以完成NN的输出值的计算。

• 在多个样本上实现计算过程向量化

那么，我们如何对多个样本同时进行向量化计算呢？

如果是对m个样本进行for循环逐个计算的话，步骤如下：

而现在，我们尝试将m个样本放入(stacked up horizontally)到一个矩阵中：

• 证明多样本计算向量化的正确性

我们要在此证明一下上述向量化计算方法的正确性。

如下图，我们将原本分别对不同样本进行的计算，放到一起（为了简化，把b项全部置为0）：

那么，原本需要for循环在m各样本上迭代的计算，就简化成了下图下面部分的向量化计算：

激活函数（Activation Functions）

到目前为止，我们只在使用sigmoid函数作为神经元的激活函数（ f(x)=11+e−x ），它比较适合做二分类结果输出层的激活函数（因为二分类的输出结果只能是0，1之间的值），但是激活函数还可以有一些其它的形式。

其它的激活函数还包括：

• tanh(x)= ez−e−zez+e−z ：该函数往往在实际效果中比sigmoid函数好，原因后面细说。不过该函数和sigmoid函数的一个共同缺陷是，当z的值很大或者很小时，两个函数的到数值都变得很小，趋近于0，这会导致梯度下降的速率变慢。
• ReLU（x）=max(0,x):Rectified Linear Unit，中文名为修正线性单元。它还有一些变形，如leadky ReLU.用ReLU作激活函数往往可以使得NN的学习速率比使用tanh和sigmoid快，因为ReLU的到数值在输入值大于0时总是为1，这使得参数的更新速度比较快。

而在实际的使用过程中，我们要选择的除了神经元的激活函数以外，还有NN的架构（隐藏层数目及每个隐藏层的神经元数目），

• 为什么要用非线性的激活函数

我们举例看一下如果用线性的激活函数（linear activation function）会有什么结果。

假设我们的激活函数为g(z)=z，那么如下图，我们计算NN输出值的过程：

通过公式的推导，我们会发现，如果只用线性激活函数，无论叠加多少层隐藏层来处理输入，我们最后获得的结果只能是输入向量的一个线性变化的值，也即无法对复杂的非线性模式进行捕捉。那么多层隐藏层也就失去了它的意义，因为一层隐藏层就完全可以拟合出线性的结果。

• 激活函数的导数

  • sigmoid

g(z)=11+e−x

g′(z)=ddzg(z)=g(z)(1−g(z))

• tanh

g(z)=tanh(z)=ez−e−zez+e−z

g′(z)=ddzg(z)=1−(tanh(z))2

• ReLU和Leaky ReLU

ReLU:

g(z)=max(0,z)

g′(z)=

{0 1 if z<0ifz≥0

Leaky ReLU:

g(z)=max(0.01z,z)

g′(z)=

{0.01 1 if z<0ifz≥0

NN的梯度下降

上述关于如何计算激活函数导数都是为了本节了解NN的梯度下降（简称GD）过程做的铺垫。

NN进行GD的公式推导如下：

于是，我们需要计算成本函数J针对各参数的导数值，计算的公式推导如下：

我们的计算过程分为两个步骤：

• Forward Propagation 前向传播：即之前讲的给定输入，计算NN输出的过程。
• Backpropagation 逆向传播：得到前向传播的结果，计算其与真实值之间的误差，反向求导。

随机初始化

在LR模型里面，我们在训练模型之前会将各个参数初始化为0。但在NN里面这样做是不行的，原因如下：

即这会导致同一隐藏层的每个神经元都输出相同的值，那么当对它们的权重矩阵进行更新时，每个参数的更新幅度也相同，那么同一层的神经元彼此之间就没有区别了！

因此，我们要对参数进行随机初始化。具体而言，我们利用numpy内置的函数，对参数（主要是连接权重矩阵）进行随机初始化，使其初始值为尽可能小的互不相同的非0值。

而为什么要初始化为尽可能小的非0值是因为，如果初始值比较大，正向传播的计算过程中， a[i]=g[1]∗(z[1])=w[1]x+b[1] 的值也会比较大，在sigmoid和tanh函数中，由于其导数值在函数值较大处的地方都比较小，这会导致梯度下降的速度非常慢。