DNN训练技巧(Tips for Training DNN)
本博客是针对李宏毅教授在Youtube上上传的课程视频《ML Lecture 9-1:Tips for Training DNN》的学习笔记。
课程链接
- Recipe of Deep Learning
- 训练集上效果差
- 换激活函数New activation function
- 自适应学习率Adaptive Learning Rate
- 训练集上效果好的基础上测试集上效果差
- 早停Early Stopping
- 正则化Regularization
- Dropout
- 训练集上效果差
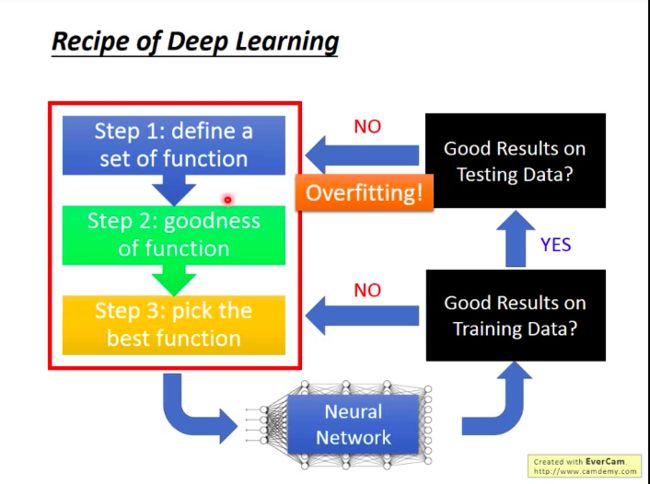
Recipe of Deep Learning
如下图:了解DL的三步骤;三步做完之后,获得一个NN,接着检查所得到的模型,根据检查的结果执行相应的措施。
对于DL来说,过拟合往往不是你首先会碰到的问题,反而是训练过程就很难得到满意的结果,即可能训练集上的准确率就一直很低。如果你在训练集上准确率很高了,但在测试集上准确率低,那才是过拟合。
所以,不要总是第一时间认为测试集上效果不好是因为过拟合!
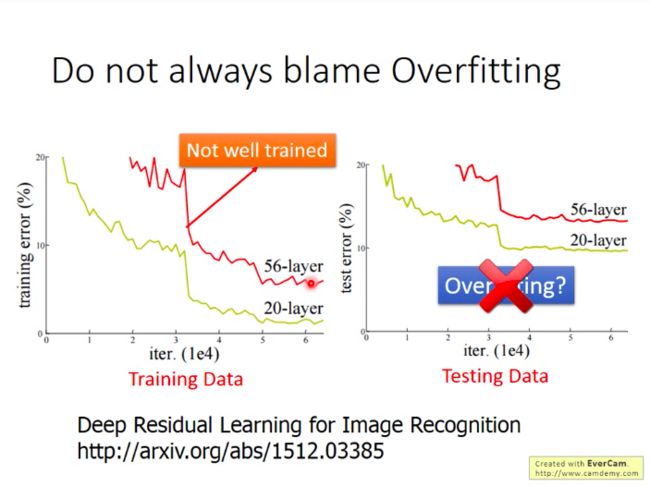
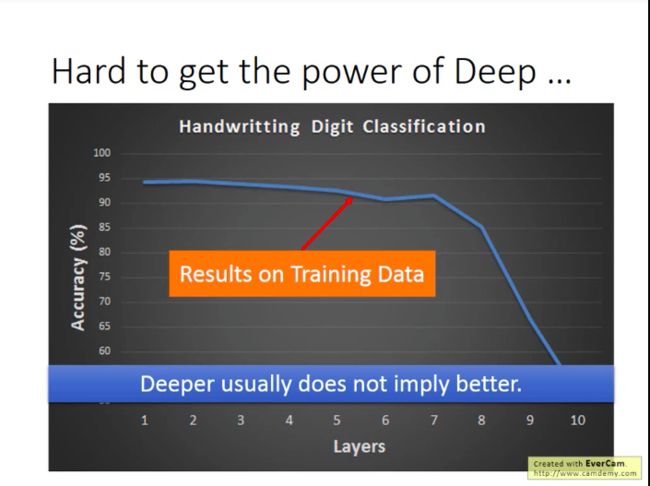
生动的例子看下图:光看测试集上的表现,很多人会直觉地认为“哎哟,你看56层效果这么差,估计就是过拟合了,根本用不到那么多参数~~”。
可是,下结论之前,我们再看看这两个模型在训练集上的表现:
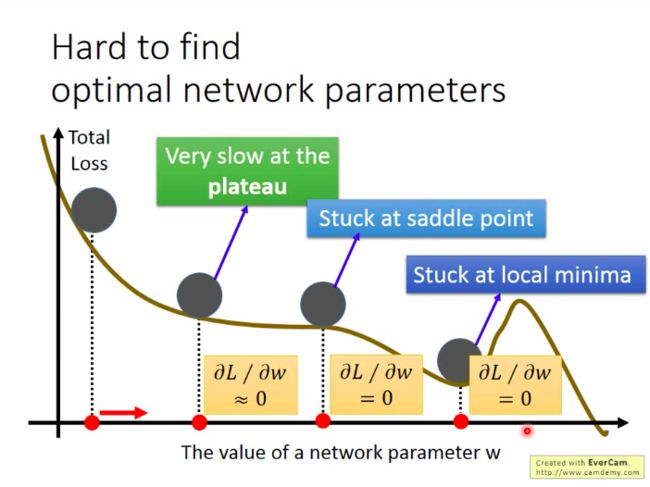
结果发现,56层的网络在训练集上表现也是比较差的,那么也就是说,56层的网络本身连训练都没做好,更别谈测试了!!!而造成这种现象的可能原因很多:
- 局部最小(local minima)
- 鞍点(saddle point)
- 停滞(plateau)
- ……
李老师同时也提出,这也不太可能是欠拟合问题,因为欠拟合一般是指模型的参数不够多,所以其能力不能解出这种问题。但是明明参数比56层网络少的20层网络也可以在训练集上达到更好的效果,所以不应该是欠拟合/模型的能力问题。
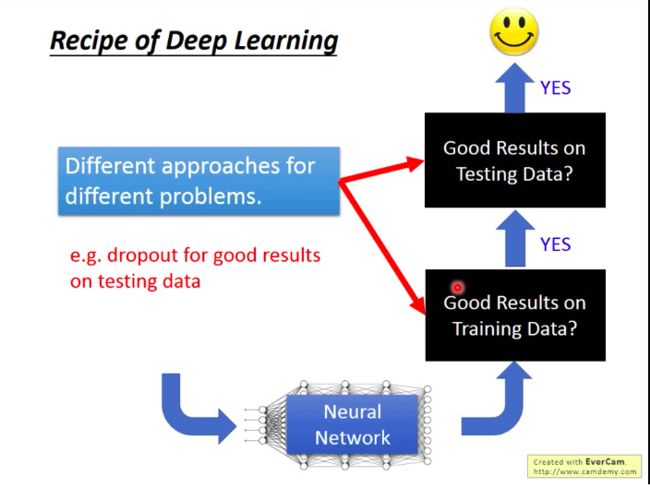
李老师提醒:读文献时,看到新方法时,要明白它是要解什么样的问题?一般DL要解决的问题就是训练集上的准确率和测试集上的准确率这两个问题,而新提出的方法也一般是针对这两个问题。
比如Dropout手段是用来提升模型在测试集上的准确率的,如果你是在训练集上准确率低,那用dropout就根本就是南辕北辙!所以请注意对症下药!
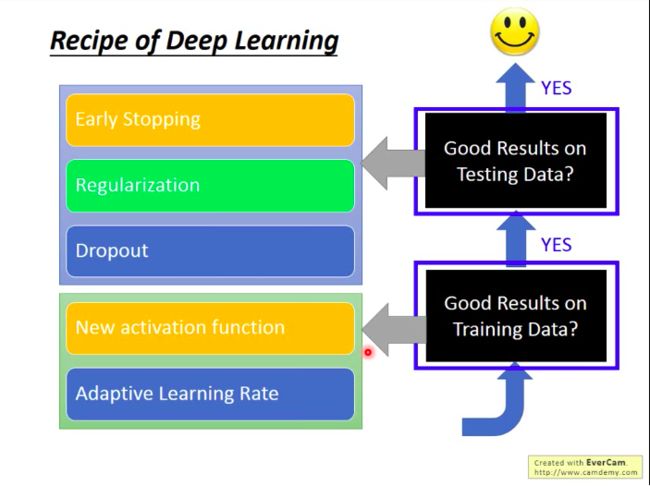
那么,针对两个典型DL问题,解决方法有哪些呢?见下图:
训练集上效果差?
换激活函数(New activation function)
例子:在MNIST上的网络,如果用sigmoid激活函数,则当层数越多时,效果反而越差!
有可能有人一看,就觉得“啊!9层10层参数太多,过拟合了!”
Naive!其实上图的线就是在训练集上的表现!(李老师随后用keras实际演示了一下)
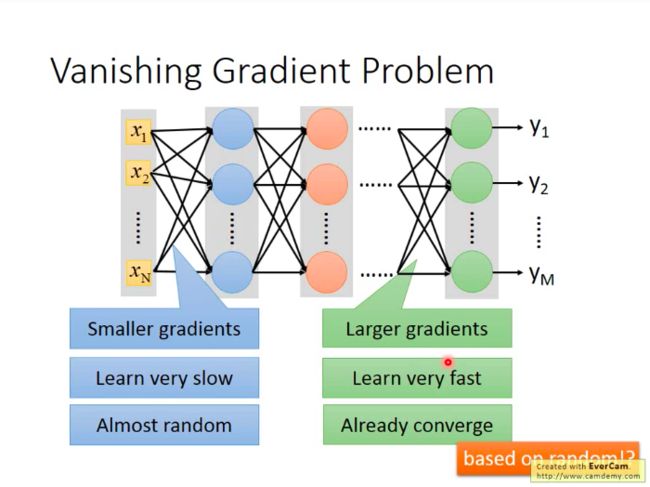
原因:梯度弥散(Vanishing Gradient Problem):在靠近input的部分梯度较小,在远离input的地方,梯度较大。因此,靠近input的参数更新慢、收敛也慢,远离input的参数更新快、收敛得也很早。
为什么会有这个现象发生呢?
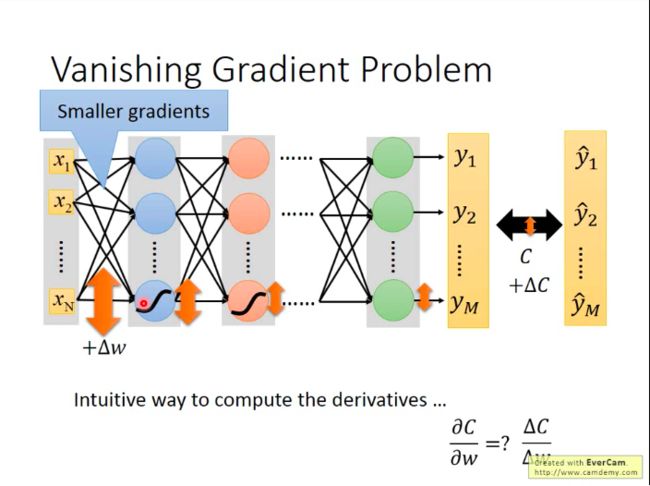
如果我们把BP算法的式子写出来,就会发现:用sigmoid作为激活函数就是会出现这样的问题。
直觉上想也可以理解:某个参数的下降梯度取决于损失函数对参数的偏导,而偏导的含义是:当该参数变化很小一点,对应的损失函数向相应变化的幅度。所以我们假设对第一层的某个参数加上△w,看它对损失函数值的影响。那么,当△w经过一层sigmoid函数激活时,它的影响就会衰减一次。(sigmoid会将负无穷到正无穷的值都压缩到(-1,1)区间)
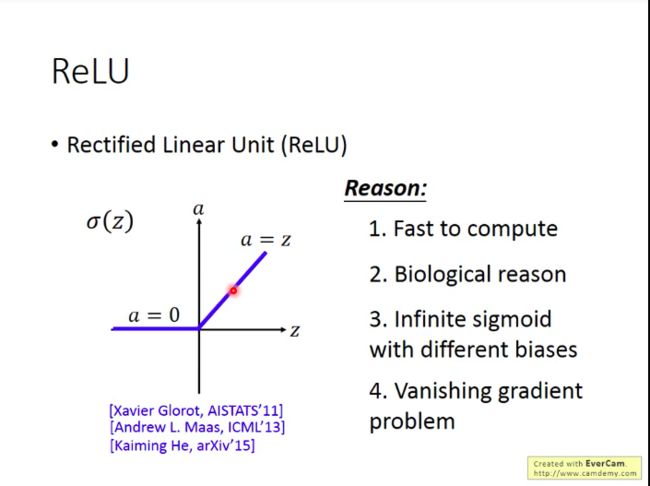
于是,怎么解决这个问题呢:换一个不会逐层消除掉增量的激活函数,比如ReLU.
而且除了解决梯度弥散问题,ReLU含有其它的好处:
- 计算速度快
- 生物学层面的理由
等同于无穷多层的偏差不同的sigmoid函数叠加的结果
那ReLU具体怎么解决梯度弥散问题呢?
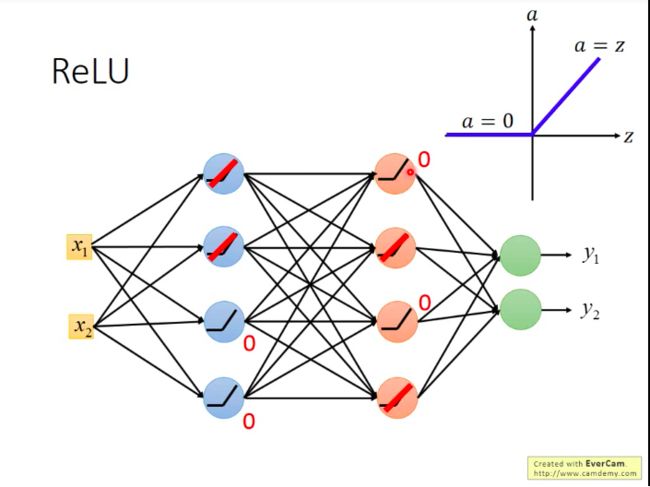
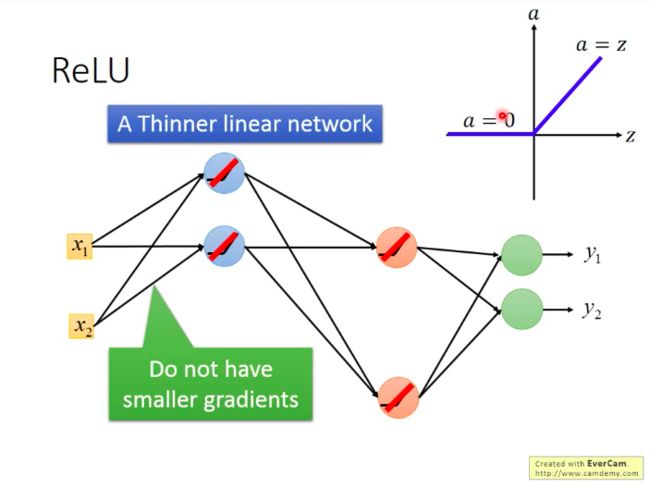
如下图,假设图中网络的激活函数都是ReLU。而网络中必然有一些神经元对应的输出会是0,它们对于网络的贡献也是零,故可以逻辑上直接从网络中删除,这样我们就获得了一个“更瘦长”的线性网络(输出等于输入)。
而之前说梯度递减也是因为sigmoid的衰减效果,而我们现在用ReLU它本身不会对增量进行递减,因为现在凡是在网络中work的神经元,其输出都等于其输入,相当于线性函数y=x。
问题:如果网络都用ReLU了,网络变成了线性的了?那NN的效果不会变得很差吗?这与我们使用深层网络的初衷不是违背了吗?
答:其实使用ReLU的NN整体还是非线性的。当每个神经元的操作域(operation region)是想相同的时,它是线性的。即当你对input只做小小的改变,不改变神经元的操作域,那NN就是线性的;但如果对input做比较大的改变,改变了神经元的操作域,这样NN就是非线性的了。
另外一个问题:ReLU不能微分呀?怎么做梯度下降呀?
答:当x>0时,ReLU微分就是1,当x<0时,ReLU微分就是0。而x的值一般不太可能恰好是0,所以不在意x=0时的微分值也没问题。
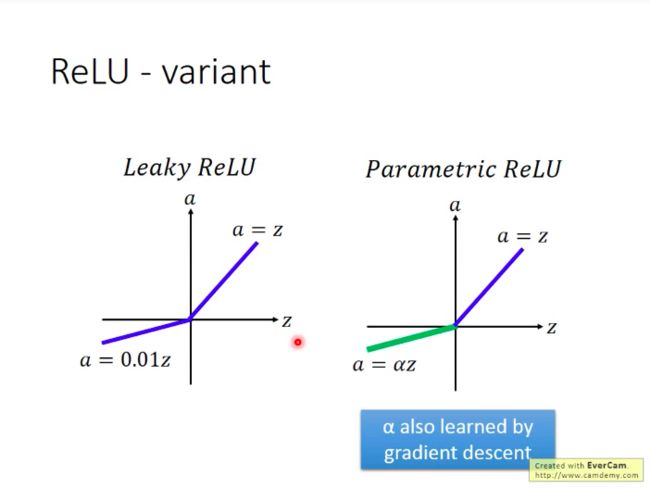
ReLU的变形
原本的ReLU在参数小于0时,因为梯度等于0,就停止了更新。为了让参数保持更新,可以适当改变ReLU在负轴的形态。(leaky ReLU, Parametric ReLU)
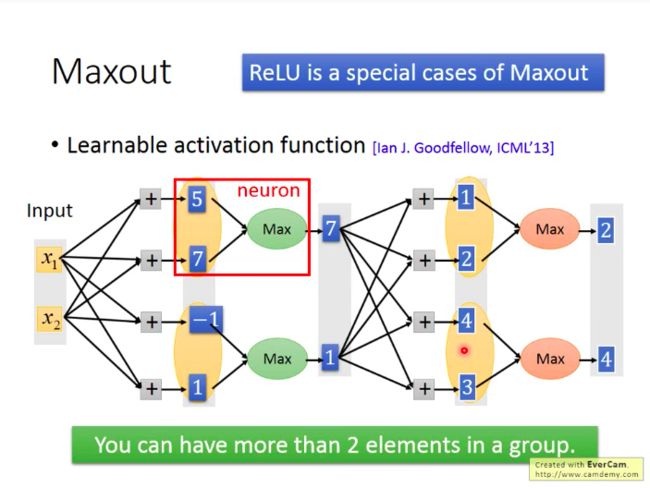
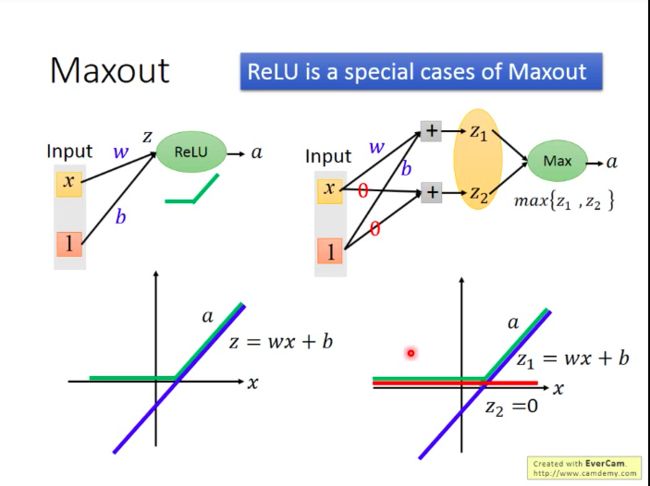
有没有ReLU以外的好的激活函数形式:Maxout(ReLU是maxout的一种特例)
Maxout如何做到和ReLU一样的效果?
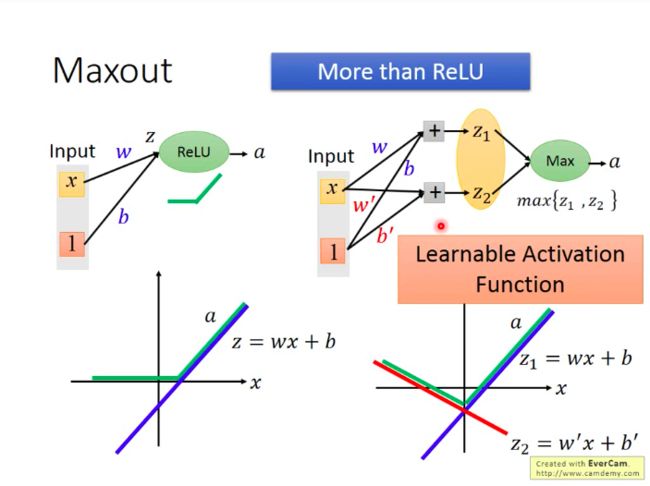
如下:Maxout也可以超越ReLU:Learnable Activation Function
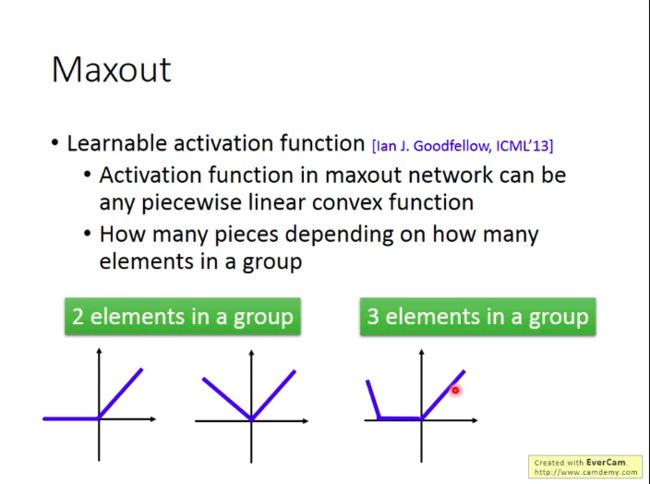
Maxout的激活函数可以是任意分片线性凸函数,分片数量取决于将多少个元素分为一组:
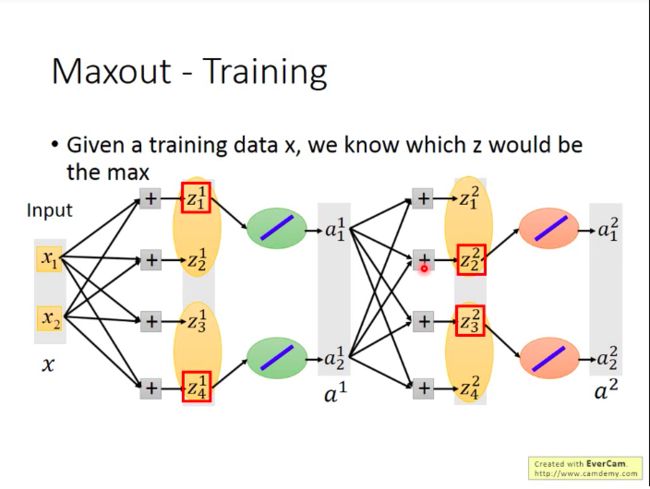
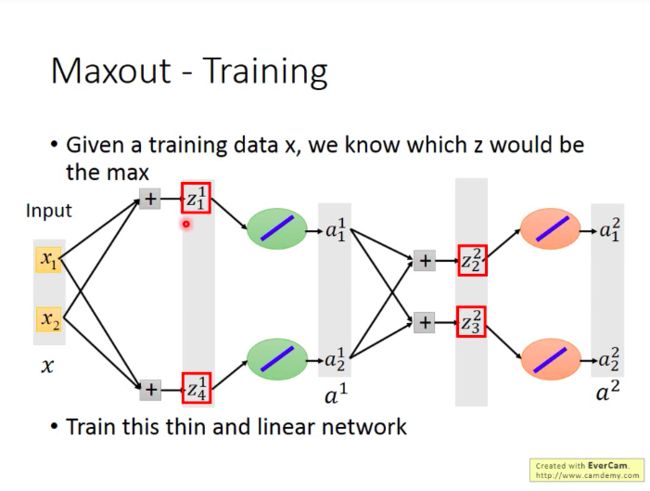
问题:Maxout网络怎么训练?
其实Maxout网络因为是从group里面选取值最大的元素,那么那些未被选中的neuron的贡献就可以看做是0,可以拿掉。那么Maxout也就称为一种类似于线性的激活函数(直接将输入值输出)。所以我们直接训练拿掉了未被选中的neuron后的”瘦长“网络就可以。
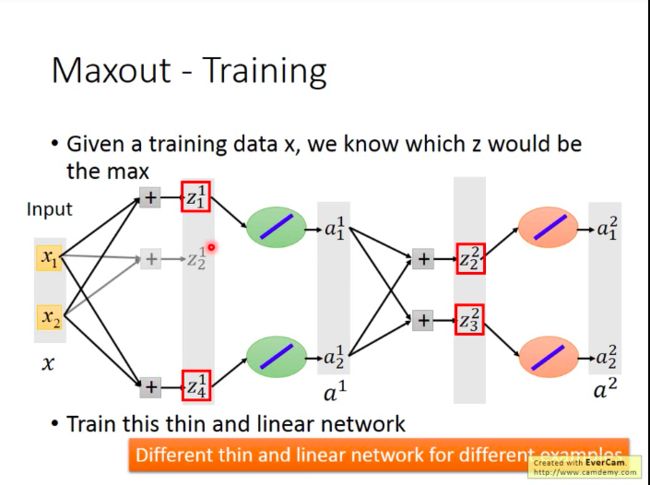
另外,不用担心这样会造成那些为被选中的neuron的参数无法被训练到,因为其实你每次输入的训练数据不同时,被选中的neuron也不同,所以终究而言,所有的neuron都是能被训练到的。
自适应学习率(Adaptive Learning Rate)
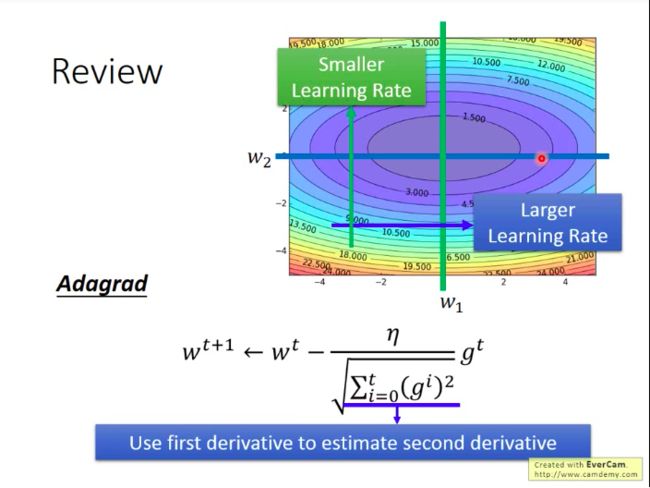
Adagrad
有会变化的学习率,变化的方式是每次的原本学习率除以过去所有更新所用的梯度的平方和的算术平方根,用公式表达如下:
wt+1<−wt−ηΣti=0(gi)2gt在图上来看,adagrad的含义是:对于梯度一般比较小的参数,我们给它较大的学习率;对于梯度一般比较大的参数,我们给它较小的学习率。
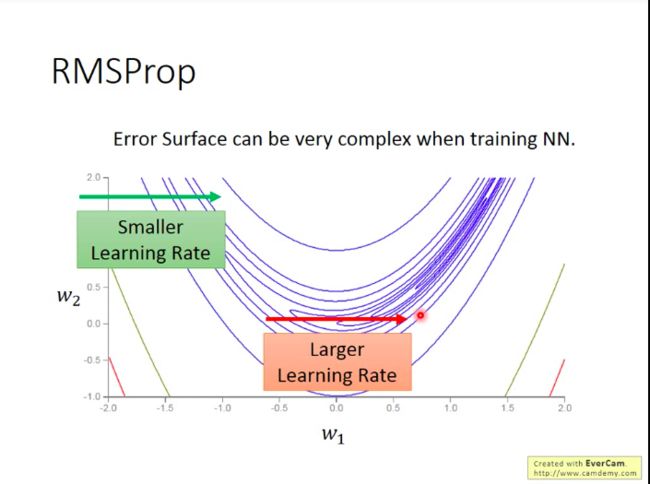
但是也有可能有Adagrad无法处理的问题:因为像logistic regression里面,我们的损失函数是一个凸函数的形状,但是在DL里面,很有可能损失函数是各种形状:
如下图,这样一种”月形“的损失函数上, w1 的更新我们需要它在平坦的区域给它较小的学习率,在较陡峭的地方,给它较大的学习率,即它的学习率应该是更加动态变化的,但adagrad的话只能做到单调递减的学习率。
Adagrad进阶版:RMSProp(Hinton在线上课程里提出的,没有正式paper…)
难以找到最优NN参数
前面提到,训练不好NN的可能原因有很多,包括局部最优,鞍点和停滞。
不过LeCun说过,局部最优的问题不用太担心,因为一般不会有那么多局部最优,毕竟局部最优是要求所有的损失函数维度在局部最优点都呈现山谷的形状,这个不太常见。
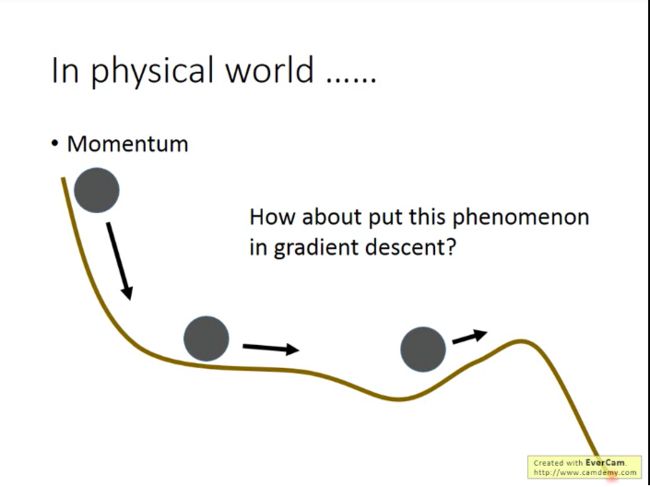
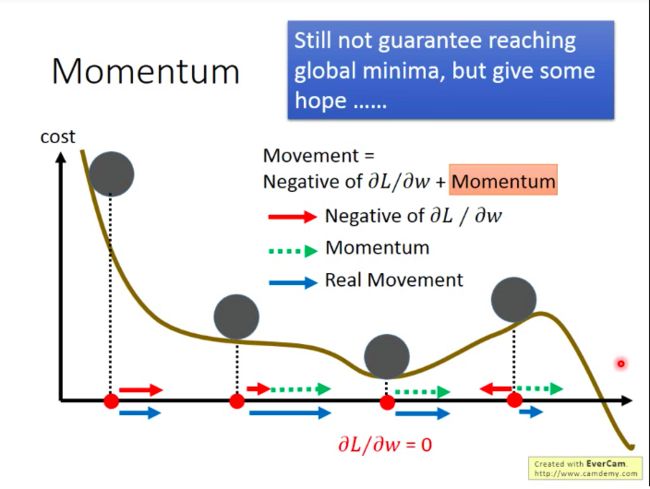
帮助解决最小值和停滞问题的技巧:动量(Momentum)
现实世界中,当一个球从高点滚落到低点,由于惯性,它有能力跨越局部最优的山谷,进而到达更低点,我们能不能借鉴这种思想呢?
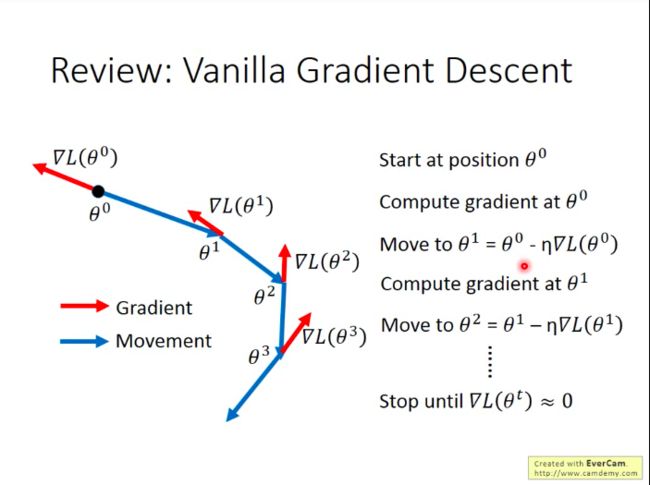
梯度下降的一般做法:
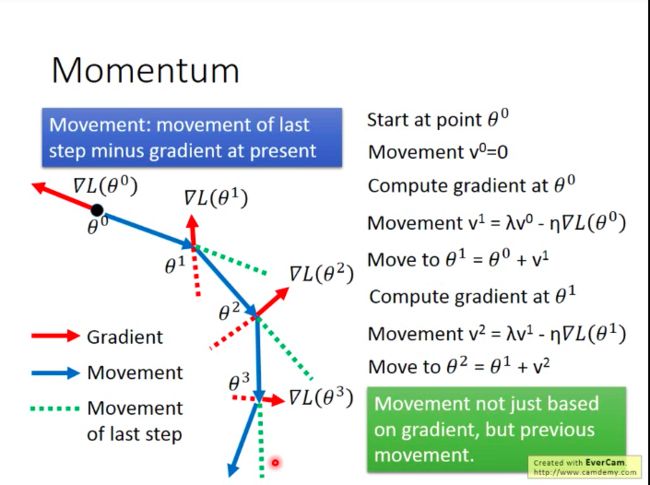
加上动量后的梯度下降的做法:我们每一次移动都由当前梯度和上一次的移动共同决定。
而 vi 实际上就是之前所有梯度的加权。
再从图像上来直观看一下动量的效果:
RMSProp + Momentum = Adam
(训练集上效果好的基础上,)测试集上效果差?
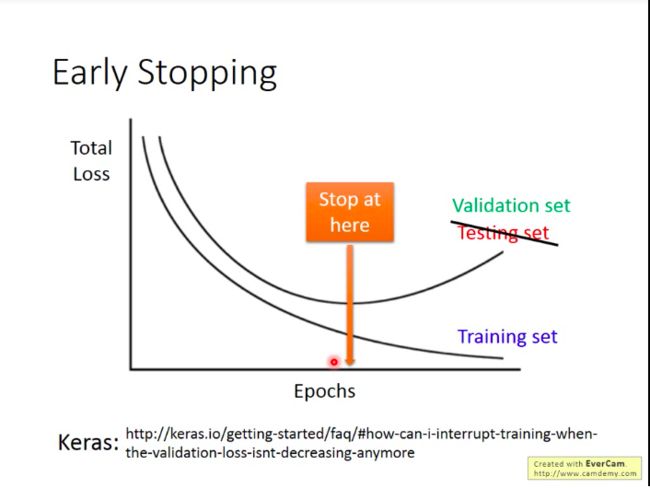
早停(Early Stopping)
我们知道,随着训练过程的逐渐进行,训练集上的损失是会逐渐降低的,但是在测试集上的损失则可能先降低再上升(开始出现过拟合)。那么,比较理想的是,如果我们知道测试集上损失的变化情况,我们就应该把训练停在测试集损失最小的位置。但是问题是:我们一般不知道测试集上的损失变化情况,所以我们常常用验证集来代替~
因此,我们这里现在讲的测试集其实是那些有标签的数据集(比如kaggle上的,自己切出来的数据等),因为我们需要计算损失。
正则化(Regularization)
我们重新定义一下要去最小化的损失函数:在原来的损失函数上加上正则项。
而( 1−ηλ )每次都是一个接近1的数,所以其实每一次更新都会使参数衰减一点。
上面是L2正则化,下面看看L1正则化:
如上图,我们可以看到L1与L2作参数更新时的差别:L1是每次参数多减去一个固定值,而L2是每次对参数进行乘以一个小于1的正值的衰减,因此L1最后会得到比较多的0值(更稀疏),而L2会得到比较多的较小但非0的值。
- 引申:人脑中的正则化
人的大脑中的神经连接数也是先增加后减少,我们可以猜测这是因为更精简的模型可以带来更好的表现。
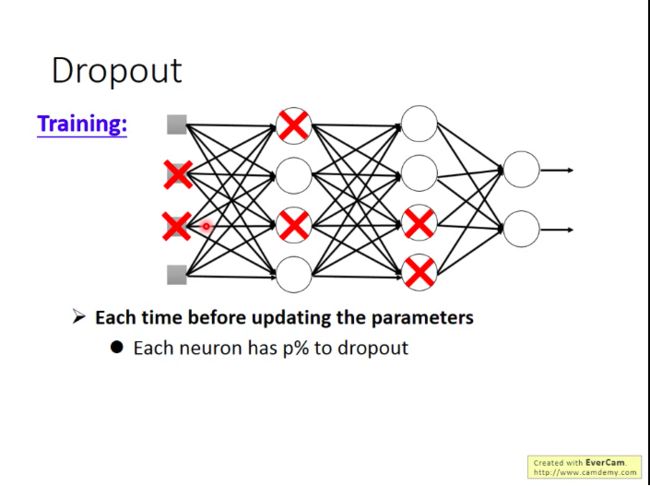
Dropout
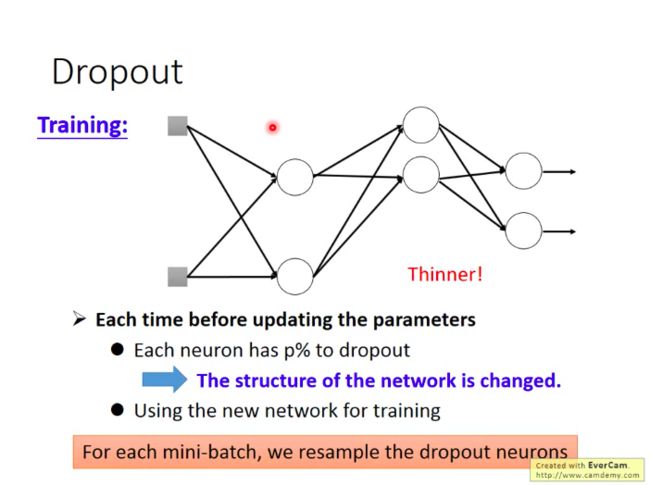
做法:训练过程中,每一次更新参数前,我们对网络中的每个神经元做一次sampling,即令每个神经元有p%的概率被丢弃掉,然后只更新余下的神经元的参数。
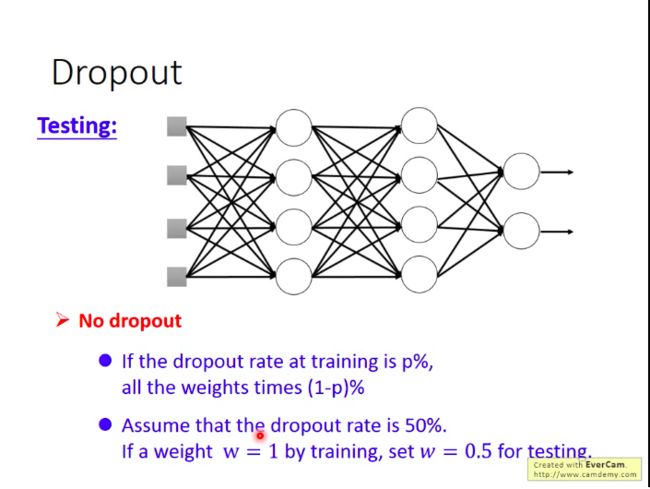
测试时怎么做呢:不做dropout!!!并对参数乘以(100-p)%。
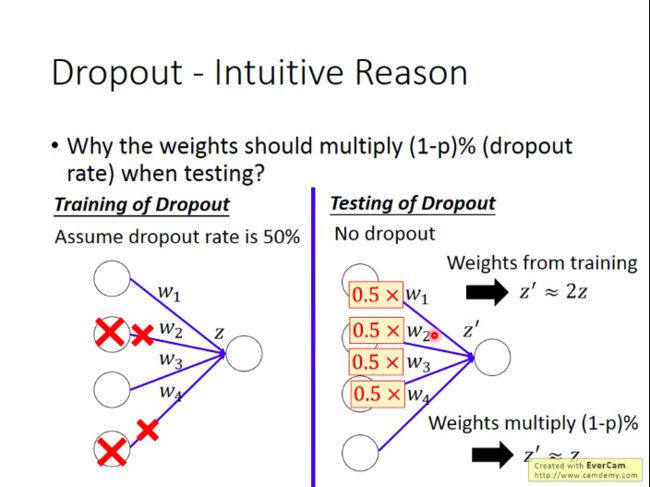
- 为什么要乘以(100-p)%?
用dropout训练时,期望每次会有p%的神经元未得到训练。而在测试集上,每次都是所有的神经元都参与了工作,所以在计算z值时,会是原来训练时的 1100−p 倍,因此需要在测试时乘以(100-p)%。
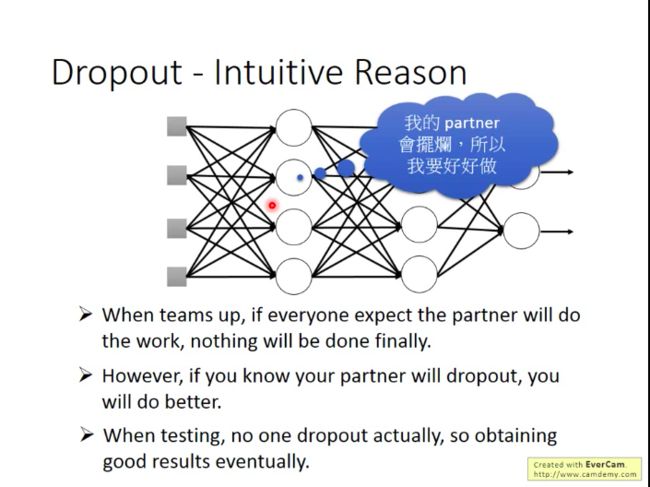
- 为什么Dropout会有效呢?
小李训练时会绑沙袋,而一放下沙袋,束缚束缚,能力就会增强。
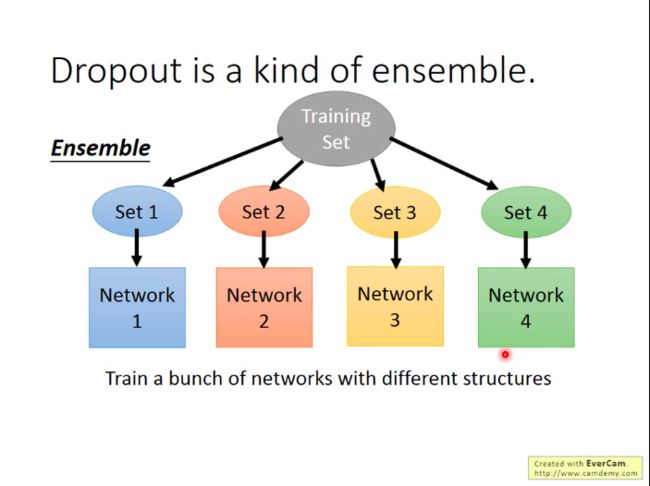
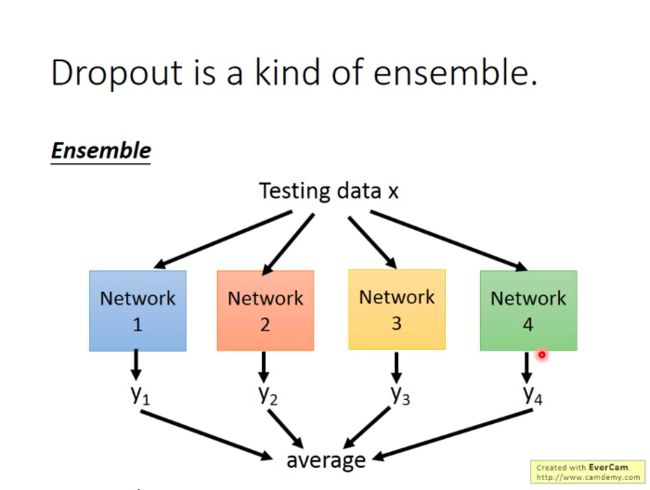
- Dropout是一种ensemble
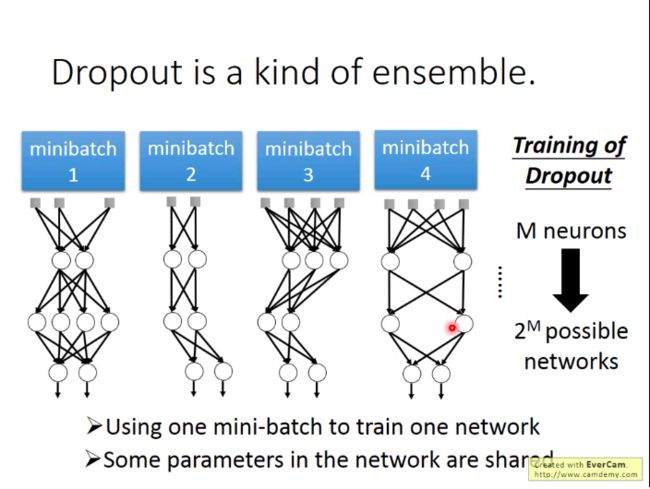
因为每次用一个minibatch的数据对NN进行训练时,由于dropout,每次都相当于训练了一个新结构的网络,那么当我们整个NN中有M个神经元时,我们最多可以训练处 2M 个可能的网络,而最终测试时,也就相当于这些网络合力给出结果。
也不用担心说一个网络只用一个batch来训练,效果会不会很差,因为神经元的参数是共享的,大家其实可以整体看做还是在合力使得彼此的能力都变得更强。
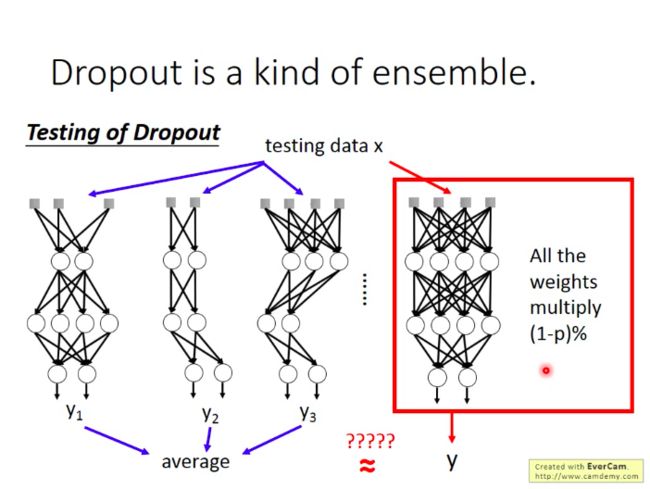
那么按理来说,我们如果这样做ensemble,最后应该把所有的网络都输入测试数据x,再取所有输出的平均作为结果,但是因为网络数量太多,这样做不太实际。而神奇的就是:当我们把所有的网络参数乘以(100-p)%,然后把测试数据x输入到原本的网络中,它的输出结果就和ensemble的结果很接近!!!
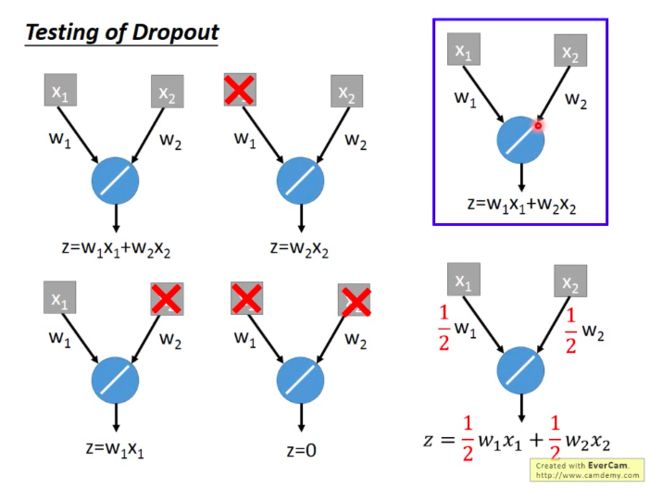
- 为什么呢?
用一下一个单一的神经元的例子就可以看出来: