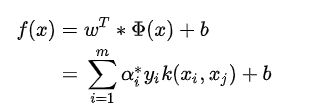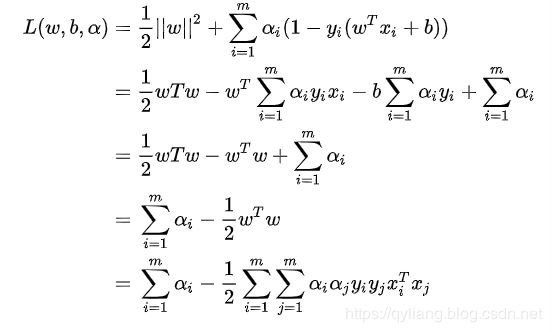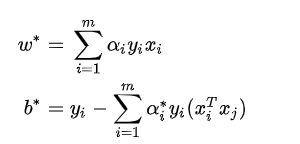【手撕】支持向量机算法（SVM）
SVM算法的基本思想就是寻找最大间隔，即寻找最合适的参数w、b使得两异类之间的间隔r最大。
一、间隔与支持向量——模型建立
令划分的超平面为 w T x + b = 0 w^Tx+b=0 wTx+b=0 ，其中w为划分超平面的法向量，决定方向；b为位移最后值，决定与原点之间的距离。
任意一点x到超平面的距离为：
r = w T x + b ∣ ∣ w ∣ ∣ r=\frac{w^Tx +b}{ ||w|| } r=∣∣w∣∣wTx+b
对于任意数据 x i x_i xi ，若分类正确，则：
{ w T x + b ≥ + 1 y i = + 1 w T x + b ≤ − 1 y i = − 1 \left \{ \begin{matrix} w^T x+b \geq +1 \ \ \ \ y_i=+1\\ w^Tx +b \leq -1 \ \ \ \ y_i=-1 \end{matrix} \right. {wTx+b≥+1 yi=+1wTx+b≤−1 yi=−1
上式中，等号成立的条件在距离超平面最近的几个点成立，那几个点也称为支持向量。
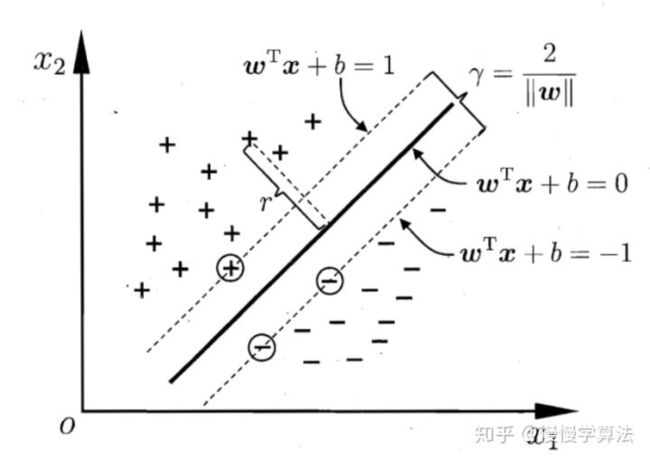
如上图所示，两个异类之间的间隔为 :
r = 2 ∣ ∣ w ∣ ∣ ； s . t . y i ( w T x i + b ) ≥ 1 , i = 1 , 2 , 3 ⋯ r=\frac {2}{ ||w|| }；s.t. y_i(w^Tx_i+b)\geq1 ,i=1,2,3 \cdots r=∣∣w∣∣2；s.t.yi(wTxi+b)≥1,i=1,2,3⋯
那么现在的任务就是找到合适的w和b，使得r最大了，直接求是困难的，需要进行问题的转化：
最大化r，就是最小化 ∣ ∣ w ∣ ∣ 2 ||w||^2 ∣∣w∣∣2 ，即基本模型可以转化为：
m i n w , b 1 2 ∣ ∣ w ∣ ∣ 2 min_{w,b}\frac{1}{2}|| w || ^2 minw,b21∣∣w∣∣2
s . t . y i ( w T x i + b ) ≥ 1 , i = 1 , 2 , 3 ⋯ s.t. y_i(w^Tx_i+b)\geq1 ,i=1,2,3 \cdots s.t.yi(wTxi+b)≥1,i=1,2,3⋯
二、对偶问题——求解模型
加入拉格朗日算子求解SVM，使模型转化为：
L ( w , b , α ) = 1 2 ∣ ∣ w ∣ ∣ 2 + ∑ i = 1 m α i ( 1 − y i ( w T x i + b ) ) α i > 0 L(w,b,\alpha )=\frac{1}{2}|| w || ^2 + \sum_{i=1}^{m}\alpha _i(1-y_i(w^Tx_i+b)) \ \ \alpha _i>0 L(w,b,α)=21∣∣w∣∣2+∑i=1mαi(1−yi(wTxi+b)) αi>0
可以看出后面以一项是小于0的，要使得 1 2 ∣ ∣ w ∣ ∣ 2 \frac{1}{2}|| w || ^2 21∣∣w∣∣2 最小，就要让 α i \alpha _i αi 尽量大。那么我们面对的标准问题就是：
m i n w , b m a x α L ( w , b , α ) min _{w,b} max _{\alpha } L(w,b,\alpha) minw,bmaxαL(w,b,α)
即在最小化w和b的情况下，尽量让 α \alpha α 大，简称“最小的最大”。
那么可以转化成对偶问题，“最大的最小”：
m a x α m i n w , b L ( w , b , α ) max _{\alpha } min _{w,b} L(w,b,\alpha) maxαminw,bL(w,b,α)
标准问题和对偶问题弄清楚了以后，就具体看看怎么解吧，实际上高数里面学到的多元微分方程的拉格朗日解法正好解决问题：也就是把w，b看成变量，然后求偏导，令偏导为0。
L ( w , b , α ) = 1 2 ∣ ∣ w ∣ ∣ 2 + ∑ i = 1 m α i ( 1 − y i ( w T x i + b ) ) α i > 0 L(w,b,\alpha )=\frac{1}{2}|| w || ^2 + \sum_{i=1}^{m}\alpha _i(1-y_i(w^Tx_i+b)) \ \ \alpha _i>0 L(w,b,α)=21∣∣w∣∣2+∑i=1mαi(1−yi(wTxi+b)) αi>0
{ w − ∑ i = 1 m α i y i x i = 0 − ∑ i = 1 m α i y i = 0 \left \{ \begin{matrix} w -\sum_{i=1}^{m }\alpha _i y_i x_i =0 \\ - \sum_{i=1}^{m }\alpha _i y_i =0 \end{matrix} \right. {w−∑i=1mαiyixi=0−∑i=1mαiyi=0
化简得到两个关系式：
{ w = ∑ i = 1 m α i y i x i ∑ i = 1 m α i y i = 0 \left \{ \begin{matrix} w =\sum_{i=1}^{m }\alpha _i y_i x_i \\ \sum_{i=1}^{m }\alpha _i y_i =0 \end{matrix} \right. {w=∑i=1mαiyixi∑i=1mαiyi=0
那我就把原式拆开，看看我们求偏导后的两个式子能有啥用吧。
上述式子为使用求偏导后化简的结果。
那么再考虑对偶问题，就可以转化为：
m a x α L ( w , b , α ) max_\alpha L(w,b,\alpha ) maxαL(w,b,α)
即，
m a x α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j max_\alpha \sum_{i=1}^{m}\alpha _i - \frac{1}{2} \sum_{i=1}^{m}\sum_{j=1}^{m}\alpha _i\alpha _j y_iy_j x_i^T x_j maxα∑i=1mαi−21∑i=1m∑j=1mαiαjyiyjxiTxj
也就是：
m i n α 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j − ∑ i = 1 m α i min_\alpha \ \frac{1}{2} \sum_{i=1}^{m}\sum_{j=1}^{m}\alpha _i\alpha _j y_iy_j x_i^T x_j - \sum_{i=1}^{m}\alpha _i minα 21∑i=1m∑j=1mαiαjyiyjxiTxj−∑i=1mαi
现在就可以求出满足条件的 α ∗ \alpha ^* α∗ 就可以求解SVM了，求解的方法是SMO方法，大致思想是每次在优化变量中挑出两个分量进行优化让，其他分量固定。
更新参数过程为：
生成的超平面分类决策函数为：
w ∗ x + b ∗ = 0 f ( x ) = s i g n ( w ∗ x + b ∗ ) w^*x+b*=0 \\ f(x)=sign(w^*x+b*) w∗x+b∗=0f(x)=sign(w∗x+b∗)
当f(x)大于0为一类，小于0为另一类，其中sign(x)为符号函数。
三、若线性不可分——核函数
当原始数据线性不可分的时候，可以将其投影到高维空间中，这样会更容易分开。想象这样一个场景，5个白球和5个黑球在桌面上不能用一根棍子分开的时候（二维空间线性不可分），此时假设黑白球质量不一样，假设你是一个武林高手，你可以一拍桌子，让白球跳得高一点，黑球低一点，唰的扔一张纸，将黑白球完美分开，这张纸就是超平面，在三维空间中轻松分开了二维空间线性不可分的数据。
但投影之后的高维空间会更加难以运算，此时我们就需要核函数了，使用核函数来将高维特征空间的内积转化为在原始数据空间上的运算，即 k ( x i , x j ) k(x_i,x_j) k(xi,xj) 。
常用的核函数为：
值得注意的是核函数的线性组合、直积、经过函数变换之后仍然是核函数。
欢迎关注公号：慢慢学算法。