Matlab 曲线拟合之 polyfit 、polyval、poly2str 函数

原文出处（仅供参考）

ttps://www.cnblogs.com/farewell-farewell/p/7227516.html

https://www.cnblogs.com/clairvoyant/p/4710015.html

1  Matlab 曲线拟合之polyfit与polyval函数

p=polyfit(x,y,n)

[p,s]= polyfit(x,y,n)

说明：x,y为数据点，n为多项式阶数，返回p为幂次从高到低的多项式系数向量p。x必须是单调的。矩阵s用于生成预测值的误差估计。

 

多项式曲线求值函数：polyval( )

调用格式： y=polyval(p,x)

[y,DELTA]=polyval(p,x,s)

说明：y=polyval(p,x)为返回对应自变量x在给定系数P的多项式的值。

[y,DELTA]=polyval(p,x,s) 使用polyfit函数的选项输出s得出误差估计Y DELTA。它假设polyfit函数数据输入的误差是独立正态的，并且方差为常数。则Y DELTA将至少包含50%的预测值。

 

有如下数据

时间t	1900	1910	1920	1930	1940	1950	1960	1970	1980	1990	2000
人口y	76	92	106	123	132	151	179	203	227	250	281

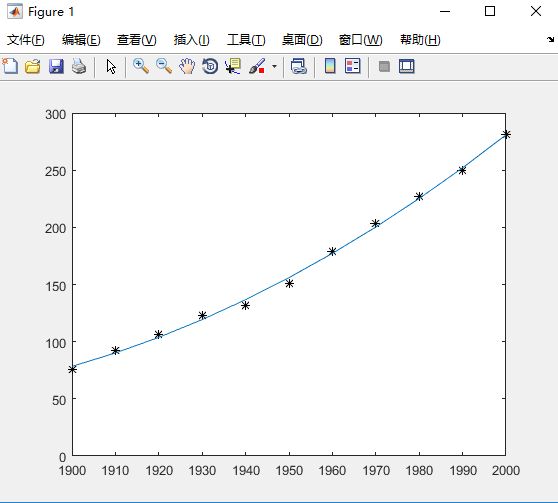
1. y与t的经验公式为 y = at^2 + bt + c

clear;
clf;                                                      %清除当前窗口
clc;
t = 1900:10:2000;                                         %时间t
y = [76 92 106 123 132 151 179 203 227 250 281];          %人口y

plot(t,y,'k*');
hold on;
% figure;       　　　　　　　　　　　　　　　　　　　　　　　　  %重新开一个图
p1 = polyfit(t,y,2);
plot(t, polyval(p1, t));
axis([1900 2000 0 300]);                                  %图像xy轴范围

disp(char(['y=',poly2str(p1,'t')],['a=',num2str(p1(1)),'   b=',...
    num2str(p1(2)),'   c=',num2str(p1(3))]));

结果如下：

y=   0.0094289 t^2 - 34.7482 t + 32061.5711
a=0.0094289   b=-34.7482   c=32061.5711

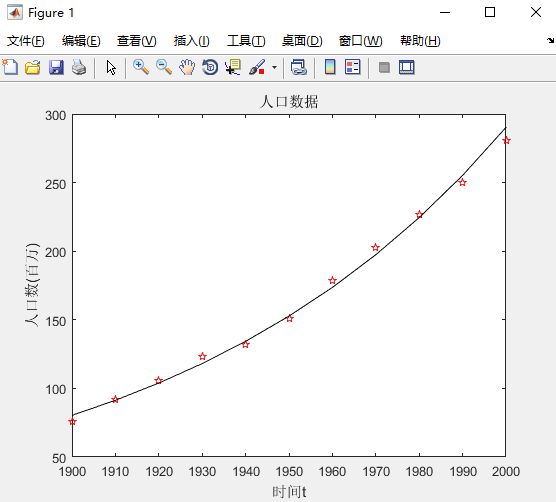
 2. y与t的经验公式为y = a e^(bt)

clear;
clf;                                                      %清除当前窗口
clc;
t = 1900:10:2000;                                         %时间t
y = [76 92 106 123 132 151 179 203 227 250 281];          %人口y
yy = log(y);                                              %指数基尼必需的线性化变形
p2 = polyfit(t,yy,1);
b = p2(1);
a = exp(p2(2));
y2 = a * exp(b*t);                                       %指数拟合函数式
plot(t,y,'rp',t,y2,'k-');
grid off;
xlabel('时间t');
ylabel('人口数(百万)');
title('人口数据');

 

2  str2poly()和poly2str()

　　　　　                         　多项式表示法

　　MATLAB中采用行向量来表示多项式，将多项式的系数按降次幂次序存放于行向量中。即多项式P(x)=a0xn+a1xn-1+ ... +an-1x+an的系数行向量为P=[a0 a1 ... an],顺序为高次幂到低次幂。举个例子，x5-7x3+2x+4，可以用系数行向量[1 0 -7 0 2 4]来表示，多项式中缺少的次幂要用“0”补齐。

　　1、str2poly():

　　下面为str2poly()函数，实现从多项式的字符串表示转换为多项式的行向量表示，输入不必降幂排列，代码如下：

 1 %sr2poly.m
 2 %把多项式的字符串表示转换为行向量
 3 function Y=str2poly(X)
 4 %X是字符串形式的多项式
 5 %Y是行向量形式的多项式
 6 %输入格式检查
 7 if(ischar(X)==0),
 8     disp('输入错误：输入X必须是一个字符串');
 9 end;
10 %用正则表达式寻找'+'或者'-'的下标位置
11 index=regexp(X,'\+|\-');
12 %多形式的项数
13 L=length(index);
14 %用于存储多项式的每一项信息的单元字符串矩阵
15 term=cell(1,L+1);
16 term(1)=cellstr(X(1:(index(1)-1)));
17 for i=1:L-1,
18     term(i+1)=cellstr(X(index(i):(index(i+1)-1)));
19 end;
20 term(L+1)=cellstr(X(index(L):end));
21 %如果第一项为空则删除第一项
22 if(isempty(char(term(1)))),
23     term(1)=[];
24     %多项式的项数减一
25     L=L-1;
26 end;
27 %多项式系数矩阵
28 coefficient=[];
29 %多项式幂次矩阵，它与多项式系数矩阵一一对应
30 power=[];
31 for i=1:L+1,
32     %单项多项式字符串表达式
33     substring=char(term(i));
34     %用正则表达式，寻找字符串'x^',由于'^'是正则表达式中特殊字符，多以用'\^'
35     index2=regexp(substring,'x\^');
36     if(isempty(index2)==0),
37         %如果匹配上
38         if((index2(1)==1))
39             %单项多项式字符串为'x^*'形式
40             coefficient=[coefficient 1];
41             power=[power str2num(substring((index2(1)+2):end))];
42         elseif(index2(1)==2)
43             %单项多项式字符串为'+x^*'或者'-x^*','3x^*'形式
44             if(substring(1)=='+'),
45                 coefficient=[coefficient 1];
46                 power=[power str2num(substring((index2(1)+2):end))];
47             elseif(substring(1)=='-'),
48                 cofficient=[coefficient -1];
49                 power=[power str2num(substring(index2(1)+2:end))];
50             else                  51                 coefficient=[coefficient str2num(substring(1:(index2(1)-1)))];
52                 power=[power str2num(substring((index2+2):end))];
53             end;
54         else
55             %单项多项式字符串为'2.2x^'
56             coefficient=[coefficient str2num(substring(1:(index2(1)-1)))];
57             power=[power str2num(substring((index2+2):end))];
58         end;
59     else
60             %单项多项式字符串不含'x^'
61             %用正则表达式，寻找字符串'x'
62             index2=regexp(substring,'x');
63             if(isempty(index2)==0),
64                 %如果匹配上'x'
65                  if(index2(1)==1),
66                      %单项多项式字符串为'x*'形式
67                      coefficient=[coefficient 1];
68                      power=[power 1];
69                  elseif(index2(1)==2),
70                      %单项多项式字符串为'+x'或者'-x','3x*'形式
71                      if((substring(1)=='+')==1),
72                          coefficient=[coefficient 1];
73                          power=[power 1];
74                      elseif(substring(1)=='-'),
75                          coefficient=[coefficient -1];
76                          power=[power 1];
77                      else
78                          %单项多项式字符串为'2.2x*'
79                          coefficient=[coefficient str2num(substring(1:(index2-1)))];
80                          power=[power 1];
81                      end;
82                  else
83                      coefficient=[coefficient str2num(substring(1:(index2-1)))];
84                      power=[power 1];
85                  end;
86             else
87                 %单项多项式字符串不含'x^','x',则断定他是常数项
88                 coefficient=[coefficient str2num(substring)];
89                 power=[power 0];
90             end;
91         end;
92     end;
93     %合并同类项
94     N=max(power)+1;
95     Y=zeros(1,N);
96     for i=1:N,
97         index3=power==(N-i);
98         Y(i)=sum(coefficient(index3));
99      end;

　　在命令行输入以下代码：(输入时为字符串形式)

 1 >> str2poly('x^7-2x^6+3x^5-5x^4+x^2-1') 

　　输出代码如下：

1 ans =
2 
3      1    -2     3    -5     0     1     0    -1

　　2、poly2str():

　　接下来是poly2str()函数，实现了把一个行向量表示的多项式转换为常见的字符串表示的多项式，代码如下：

 1 %poly2str.m
 2 %把多项式的行向量表示转换为字符串表示
 3 function Y=poly2str(X)
 4 %X是表示一个多项式的向量
 5 %Y多项式的字符串表示
 6 %输入检查，如果X不是一个向量则退出
 7 if isvector(X)==0,
 8     disp('输入错误：输入X不是一个向量，请输入一个代表多项式的向量！');
 9     return; 
10 end;
11 Y='';    %输入字符串
12 n=length(X);
13 for i=1:n,                  %把多项式的每一次幂转换成字符串
14     if(i~=1&&X(i)>0)         
15         Y=[Y '+'];          %若为正系数，必须添加‘+'
16     end;
17                              %输出系数
18     if(X(i)==0),             %如果该次幂系数为零，则不输出字符串
19         continue;
20     elseif(X(i)==1&&i~=n),   %如果该次幂系数为1，可以不输出系数，只输出想x^n
21         Y=Y;
22     else
23         Y=[Y num2str(X(i))];      %其他输入情况
24     end;
25     
26     if(i==n-1),               %输入x^n   1次幂输入字符串'x'
27         Y=[Y 'x'];
28     elseif(i==n),               %0次幂不输出x^n
29         Y=Y;
30     else
31         Y=[Y 'x^' num2str(n-i)];   %其他情况输出x^n
32     end;
33                                   %如果不是最后一项，输出'+'
34 end;
35 if(Y(1)=='+'),                    %修正如果0次幂为0时，造成末尾有多余的字符串‘+’
36     Y(1)=[];
37 end;

　　在命令行输入以下代码：(输入时为矩阵行向量形式)

 1 >> poly2str([1 -2 3 -5 0 1 0 -1]) 

　　输出代码如下：

ans = 

        x^7-2x^6+3x^5-5x^4+x^2-1