Python使用网格搜索与交叉验证的决策树算法实现波士顿房价预测（附波士顿房价数据集）

数据介绍：
数据集来自UCI机器学习知识库(数据集已下线)。波士顿房屋这些数据于1978年开始统计，共506个数据点，涵盖了麻省波士顿不同郊区房屋14种特征的信息。本项目对原始数据集做了以下处理：
• 有16个’MEDV’ 值为50.0的数据点被移除。 这很可能是由于这些数据点包含遗失或看不到的值。
• 有1个数据点的 ‘RM’ 值为8.78. 这是一个异常值，已经被移除。
• 对于本项目，房屋的’RM’， ‘LSTAT’，'PTRATIO’以及’MEDV’特征是必要的，其余不相关特征已经被移除。
• 'MEDV’特征的值已经过必要的数学转换，可以反映35年来市场的通货膨胀效应
数据集：链接：https://pan.baidu.com/s/18kcJ66dDzHTOdOlgFghgOA 提取码：20qa

第一步：导入数据

#载入此项目所需要的库
import numpy as np
import pandas as pd
import visuals as vs   # Supplementary code
 #检查你的Python版本
#from sys import version_info
#if version_info.major !=3 and version_info.minor != 7:
#raise Exception('请使用Python 3.7来完成此项目')

%matplotlib inline

#载入波士顿房屋的数据集
data = pd.read_csv('housing.csv')
prices = data['MEDV']
features = data.drop('MEDV', axis = 1)    
print("Boston housing dataset has {} datapoints with {} variables each."  .format(*data.shape))

第二步：分析数据

#目标：计算价值的最小值
minimum_price = prices.min()
print (minimum_price)

#目标：计算价值的最大值
maximum_price =prices.max()

#目标：计算价值的平均值
mean_price = prices.mean()

#目标：计算价值的中值
median_price = prices.median()

#目标：计算价值的标准差
std_price = prices.std()

#目标：输出计算的结果
print ("Statistics for Boston housing dataset:\n")
print ("Minimum price: ${:,.2f}".format(minimum_price))
print ("Maximum price: ${:,.2f}".format(maximum_price))
print ("Mean price: ${:,.2f}".format(mean_price))
print ("Median price ${:,.2f}".format(median_price))
print ("Standard deviation of prices: ${:,.2f}".format(std_price))

第三步：模型衡量标准

def performance_metric(y_true, y_predict):
    """计算并返回预测值相比于预测值的分数"""
    from sklearn.metrics import r2_score
    score = r2_score(y_true,y_predict)    
return score

def performance_metric2(y_true, y_predict):
    """计算并返回预测值相比于预测值的分数"""
    import numpy as np
    import math
    y_true_mean = np.mean(y_true)
    y_predict_mean = np.mean(y_predict)
    SSR = 0
    varX = 0
    varY = 0
    for i in range(0, len(y_true)): #多少实例
        diffxxBar = y_true[i] - y_true_mean
        diffyyBar = y_predict[i] - y_predict_mean
        SSR += (diffxxBar * diffyyBar)
        varX += diffxxBar ** 2 # 求平方然后累计起来
        varY += diffyyBar ** 2 # 求平方然后累计起来    
    SST = math.sqrt(varX * varY)
    score = SSR/SST
return score

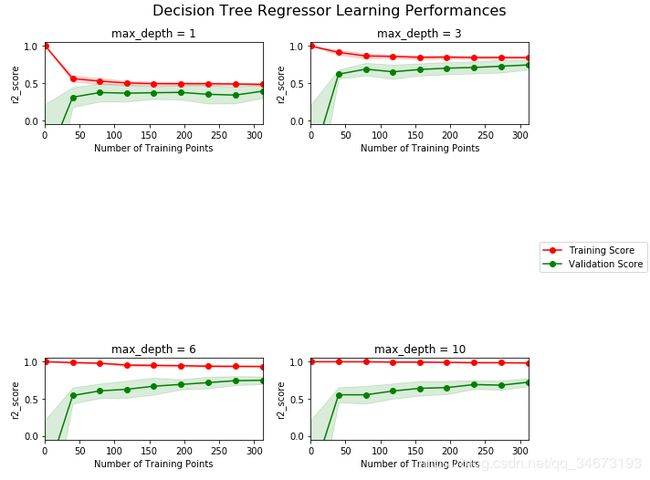
第四步：分析模型的表现（偏差方差）

#根据不同的训练集大小，和最大深度，生成学习曲线
vs.ModelLearning(X_train, y_train)

# 根据不同的最大深度参数，生成复杂度曲线
vs.ModelComplexity(X_train, y_train)

第五步：选择最优参数（网格搜索、交叉验证）

from sklearn.model_selection import KFold
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import make_scorer,accuracy_score
from sklearn.model_selection import GridSearchCV

def fit_model(X, y):
    """ 基于输入数据 [X,y]，利于网格搜索找到最优的决策树模型""" 
    cross_validator = KFold(n_splits = 10,shuffle = True, random_state = 42) #交叉验证
    regressor = DecisionTreeRegressor(random_state = 0) #决策树回归函数
    params = {'max_depth': range(1,11)}  #决策树最大深度
    scoring_fnc = make_scorer(performance_metric)   # 评分函数
    grid = GridSearchCV(regressor,params,cv = cross_validator,scoring = scoring_fnc)

    # 基于输入数据 [X,y]，进行网格搜索
    grid = grid.fit(X, y)
    # 返回网格搜索后的最优模型
return grid.best_estimator_

#基于训练数据，获得最优模型
optimal_reg = fit_model(X_train, y_train)

第六步：作出预测

# 生成三个客户的数据
client_data = [[5, 17, 15], # 客户 1
               [4, 32, 22], # 客户 2
               [8, 3, 12]]  # 客户 3
# 进行预测
predicted_price = optimal_reg.predict(client_data)
for i, price in enumerate(predicted_price):
print ("Predicted selling price for Client {}'s home: ${:,.2f}".format(i+1, price))
#计算决策系数r方
y_test_predicted_price = optimal_reg.predict(X_test)
r2 = performance_metric(y_test,y_test_predicted_price)
print ("Optimal model has R^2 score {:,.2f} on test data".format(r2))