机器学习之神经网络（机器学习技法）

神经网络的动机

感知器的线性融合

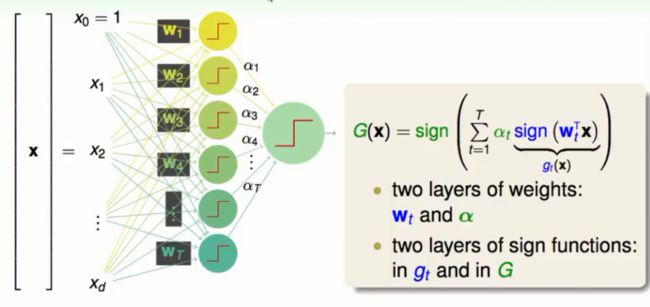
前面我们知道了将简单的模型进行融合之后会得到一个非常强大的模型。我们试着将感知器（简单的二元分类模型）做线性融合之后得到下图：

其中每一个节点都是一个感知器，其第一层的感知器都是由前一层X向量与W权重的线性组合，而第二层的感知器又是由前一层的得到的小的感知器g与新一轮的权重α线性组合而成。最后得到的线性模型如上图右所示。

用融合模型做逻辑运算

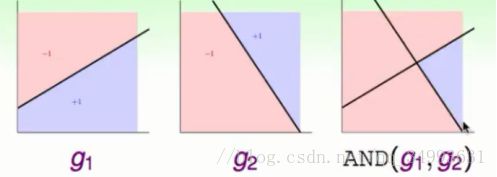
我们试着用上面的融合模型去解决两个感知器与运算的一个实例如下图所示：

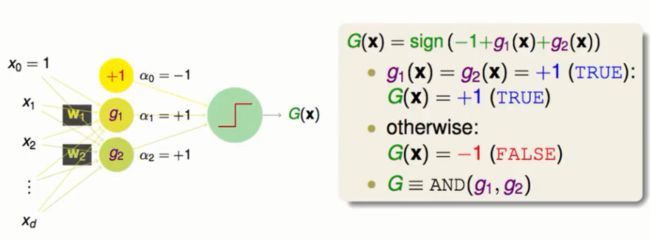
当两个模型都判定为1的时候我们的最终结果为1，其他的情况为0。再加上0维的向量我们会得到以下的融合图景：

在上面的模型中我们给定了三个维度的权重值(-1,1,1)。得到的模型为sign(-1+g1(x)+g2(x))，表达的意思就是只有两个g都判定为1的时候我们模型的值才会最终判定为1。同理我们还能解决OR(1,1,1)与NOT(1,-1,-1)的模型。

融合模型的极限

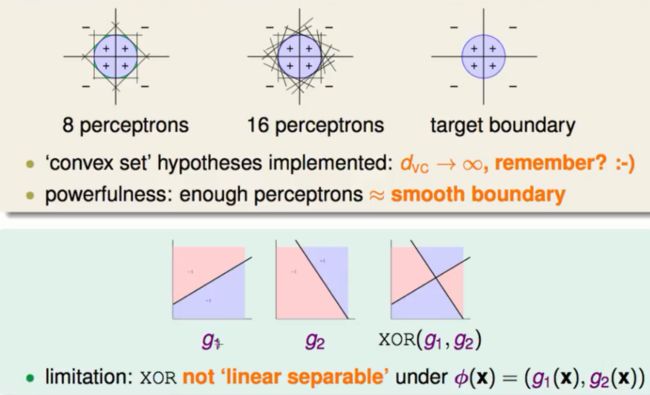
融合模型非常的强大，以致于能够分割出VC维度为无限大的凸多边形。当然这也免不了过拟合的危险。

除此之外融合模型也不是万能的比如它不能分割出一个异或的模型来如下图：

不能做出异或的原因就是如果我们把g当做是特征转换的话我们即使在转换后的空间也没有找到一个能够线性可分这笔资料的线，所以我们即使融合也无济于事。

多层的感知器：基础的神经网络

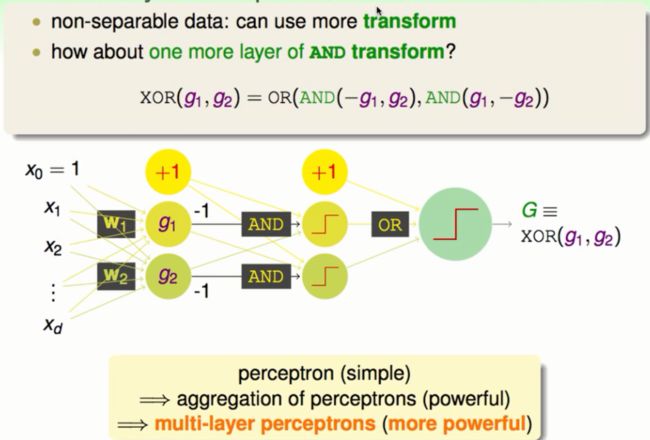
我们基于boolean逻辑运算的组合XOR(AND(-g1,g2),AND(g1,-g2))将神经网络再次扩大一层我们就可以解决上面的问题了：

由此我们可以看出，多层的感知器组合要比简单的融合更为强大，这也是神经网络的基础。

神经网络与生物学神经的关系

一句话，只是有简单的相似之处。神经网络归根结底是一个数学上的模型。就像我么造飞机一样我们只有简单的借鉴，其他的都是工程与科学的结合。我们不能做“鸟飞派”全盘的模仿。

神经网络的原理

为神经网络选择一个输出

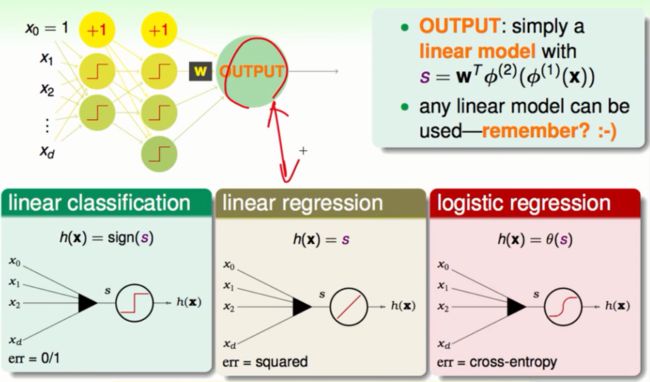
我们的最终目的就是要让输入的资料经过一层一层的转换然后经过线性的融合得到一个综合的模型。我们学过比较有代表性的线性模型就是线性二分、线性回归、逻辑回归。不同的模型会对应到每一层的转换会有不同的意义。为了计算的方便起见我们使用平方误差的线性回归：

为中间的转换选择一个函数

①不使用线性二分的函数

在前面的讨论中我们进行的是逻辑运算所以我们选择了二分函数。但是在比较复杂的问题下我们使用线性二分函数的话在最后优化的时候就会非常困难，所以不选择线性二分函数作为转换函数。

②不使用线性函数

由于我们已经选择了线性函数作为我们最后的融合模型。所以当我们转换和输出函数都是线性函数的时候我们所做的就只相当于将原来的输入只做了一个线性的融合这样的效果可想而知。没有发挥出神经网络转换与融合的特点来。

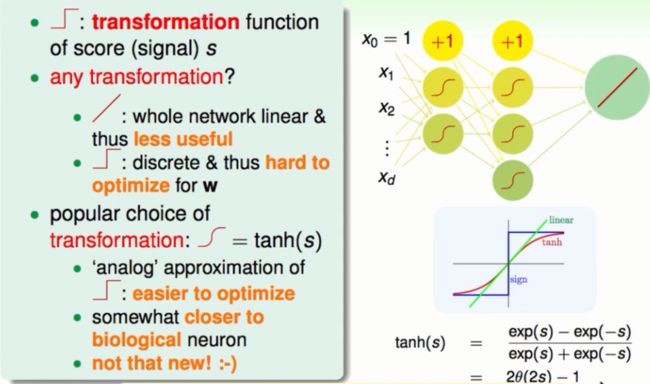
③使用tanh函数

tanh也是一个平滑的连续的s型函数。这个函数有这样的优点：首先，它比起线性二分函数更容易优化。其次，它是一个连续的函数这一点与生物学中的神经元运作很像。最后，这个函数与我们熟悉的逻辑回归函数十分相近（只是简单的平移与放缩）。

选择的过程与tanh函数如下图所示：

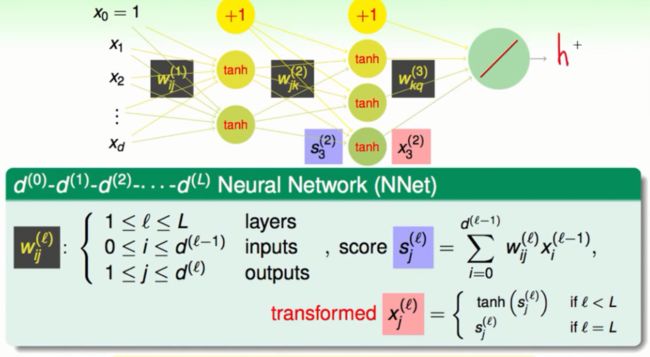
神经网络模型符号上的表示

我们把整个神经网络分为这样几个部分：

①将最原始资料输入的部分称为输入层，同时也是第0层。

②将最后输出的那一层称为输出层，同时也是第L层。

③中间不停的做转换的部分称为隐藏层，也是第l层(1<=l<=L)。

④Wij是第i层到第j层之间的权重。

⑤s是上一层的输出，也作为当前层的输入资料x。

对于每一个节点都会有一组不同的权重值，也就是对于每一个节点都会有一个不同的权重向量。

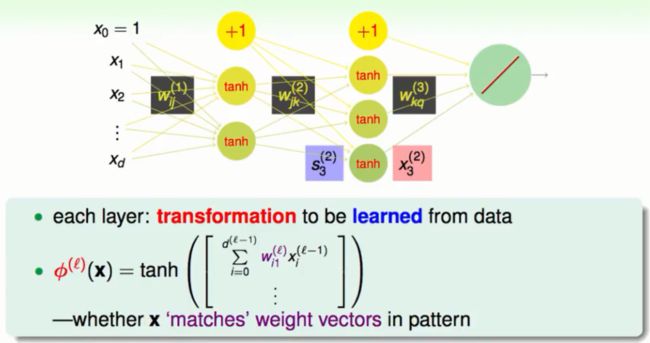
神经网络的物理意义

神经网络的节点中，每一个节点都会对应一个权重向量W。这个向量会与前面的输入所组合（透过tanh函数）组合后的输出又当做是新一轮的输入，那么这个过程就是对原来资料的一种特殊的转换。那么什么时候这个tanh函数会很大呢（也就是得到+1的结果）？就是WX内积很大的时候，内积很大说明了X与W的相似度很高，这两个向量越接近。所以我们的tanh函数很大时候的权重W就会与我们实际的数据有很高的相似性。也就是我们的W就是我们从数据中萃取出来的特性或者说是模式。

反向传播算法

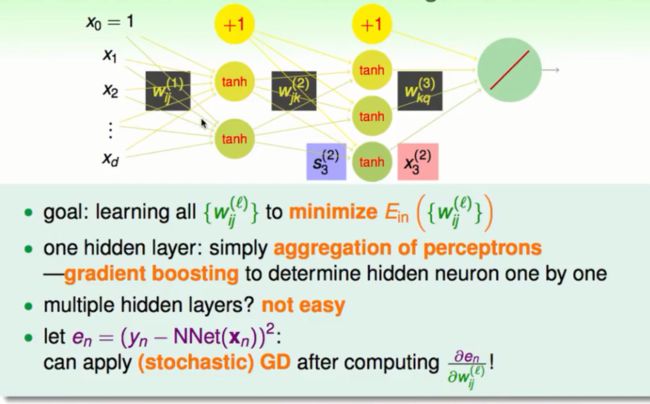
权重的决定

每一层的每个点应该对应什么权重这完全取决于我们结果的犯错误的大小，也就是损失函数的大小。我们总是希望能够有一组权重会使得我们的损失函数最小。这样的权重就是我们想要的最优权重。出于一般性的考虑我们需要知道每个节点所对应的权重（Wij）与我们最后犯的错误（en）有什么联系。也就是计算en与相对于每一个权重的偏微分，知道这个偏微分之后我们就能够知道使得错误变小的方向在哪里进而去朝这个方向更新我们的权重如下图所示：

反向传播算法

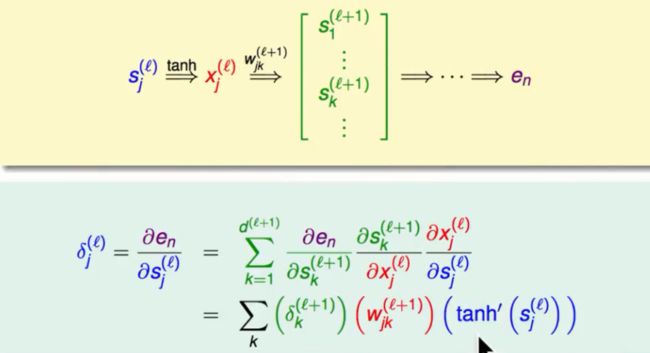
我们先计算最终的错误对于最后一层的权重的偏微分如下图所示：

我们很轻易的得到了这个关系如上图左方所示。依照这一步计算我们试图去计算en对第l层的某一个节点的权重的偏微分。其中有对第i-1层的输入X，还有一项为en对这个节点偏微分的结果我们称它为δ。我们的下一步就是计算δ。

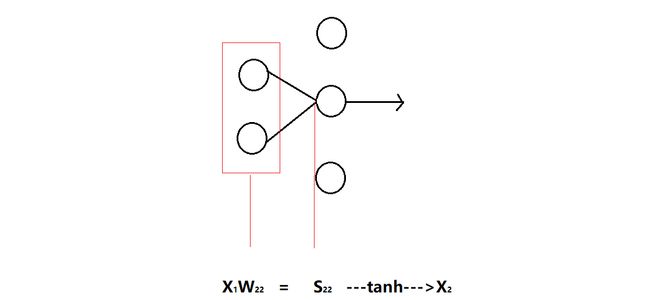
计算δ

单个节点的分数，权重与，输出关系如下：

我们继续使用微积分中的连锁率去计算δ，会得到如下的结果：

这样一来δ之间就会形成一个递推的关系，他们都能够由最后一个开始反向的计算出上一个直到地推到当前的δ为止。其中Wjk我们已经在手上了，tanh对于s的偏微分也可以计算，δ可以递推的计算出来。

这样我们得到了错误与我们一个点的权重我们也就可以重复上述步骤得到每个点对错误的影响，最后我们在根据这个影响调节每一个权重直到错误降到一个很低的值。

总的看来我们首先输入一组值得到一个错误率，然后通过错误率反过来计算每个节点对它的权重的影响，进而使用梯度下降法调节权重。整个过程我们称之为反向传播算法。如下图所示：

注意事项：

①最初的梯度我们随机给定。

②x的计算完全由首次的输入、权重与tanh函数来正向计算得来。

③在使用梯度下降法更新权重的时候每一次的更新都会将反向传播“跑一轮”比较耗时间。如果只使用一笔资料去更新的话会有一些不确定性在里面，如果使用所有的资料又显得计算量很大。所以我们选择了一个折中的方法就是选择其中的一批资料去计算梯度然后求平均，在更新的时候我们用到的梯度就是我们所求的平均的梯度。这种更新梯度的方式我们称之为mini-batch。

④最后返回的g就是从第一层开始不断做线性组合-->tanh--->多个模型融合这个过程,

g = (...tanh(Σw*tanh(Σw*x)))。

神经网络的优化

局部最小与全局最小

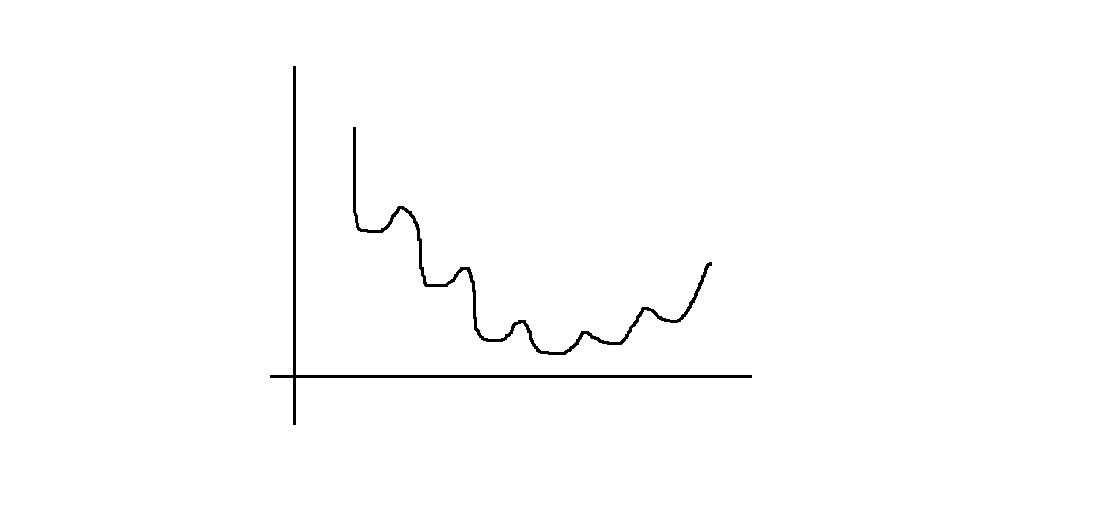
对于神经网络的优化我们使用的是梯度下降法，但是当隐藏层变多的时候我们的损失函数就变成了一个非凸函数如下图所示：

所以我们就很难使得错误率到达真正的最低点反而陷入局部最优的困境。

我们知道损失函数的最优解与我们的起始点有关，不同的起始点会有不同的最优解。一般来说权重大的时候我们的梯度较小下降速度较慢所以我们一般选择的初始权重的时候会遵循随机化与尽可能小的原则这样可能会得到更好的效果。

 

神经网络与VC维度

这里只给一个结论：dvc = (VD)，V代表神经元的数量，D代表权重的数量。这里给我们的启示就是：神经元越多我们的模型就能够做更多的事情，但是太多的神经元会使得我们有过拟合的危险。

神经网络的正则化

对于模型的正则化我们一般有L2与L1两种选择：

①单纯的选择L2的正则化，我们会使得权重变小但是只是同比的缩小，所以导致了虽然权重变小了但是大多数的权重值还不是0。这样并没有减少我们的运算量。

②单纯的使用L1的正则化，我们倒是可以得到一些稀疏的的解。但是L1的正则化下的模型是不可微分的，这样就破坏了我们神经网络可微分的体系。

③最后我们就选择了一种新的方式：将原来的L2正则化进行放缩，这次不是同比放缩而是固定的放缩。导致了一些小的权重值会趋向于0。这样我们就达到了稀疏学习的目的。改版后的正则化如下图所示：

其它的一些正则化

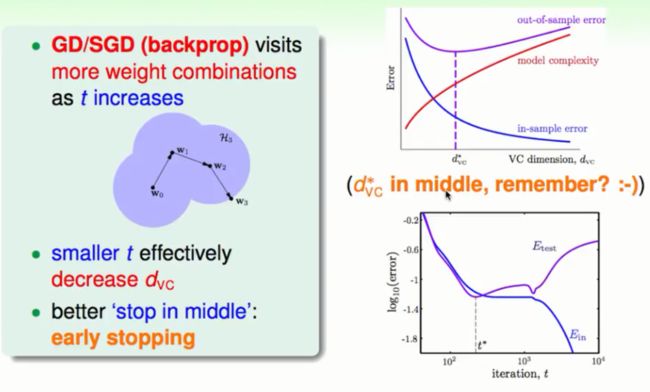
在梯度下降的过程中，我们会先看自己周围的一堆权重然后进行跟新，到了一个新的点上我们又会去执行以上相同的步骤。随着走的步数越多我们做的选择就越多，我们的复杂度就会越大也就越容易过拟合。所以我们选择早一点就停下来。

在VC里面的VC/Err图也说明了最优解不在复杂度很高的地方，也就是不在步数走的多的时候出现。

至于应该在什么时刻选择停止下来我们通常使用的就是模型检测validation。

实务上EarlyStopping的表现还是蛮不错的，如下图所示：