IMU原理与人体姿态检测
最近做了一套基于IMU的人体姿态检测系统,用来取代动作捕捉系统。一方面IMU的实时性和可开发性比动捕要好,另一方面IMU成本很低的同时精度也足以满足需求。本文介绍IMU的基本原理与基于IMU的人体姿态检测系统的设计。
1.IMU的组成与原理
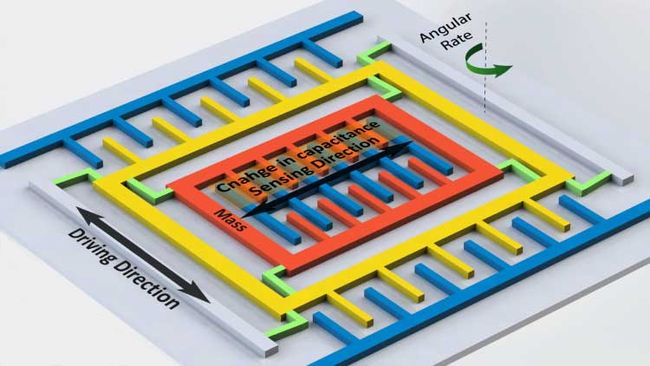
IMU可根据DOF的不同来加以区分,其中6DOF的IMU和9DOF的IMU比较常见,6DOF的IMU一般由一个三轴加速度计和一个三轴陀螺仪组成。9DOF的IMU会多一个三轴磁力计。模块所能感知状态量的个数即为DOF大小,DOF越多、精度越高的IMU也就越贵。
这里只讨论6DOF的IMU。
加速度计
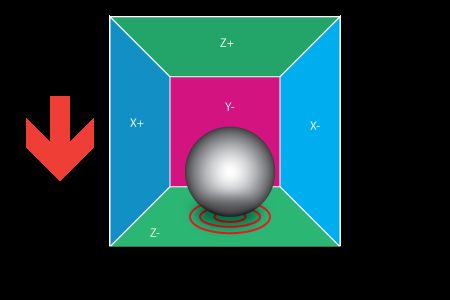
顾名思义,三轴加速度计能感受三轴的加速度,如上图中三个矢量所示。但要注意的是,当图示模块水平放置且静止,z轴方向加速度大小为-g,也就是说IMU测量的加速度与物体真实加速度相差一个重力加速度。
 ]
]
加速度计的物理实现是利用牛顿第二定律,如上图所示,中间红色物体为一个质量块,两头通过具有弹簧性质的长条结构与基底相连,红色的短栅与绿色的短栅分别为电容的极板。当基底在双箭头方向有加速度a时,由f=ma=kx,质量块会沿加速度相反的方向移动,红色极板与绿色极板之间的距离会发生变化,通过测量极板电容C的变化就可以得到加速度的大小。在三轴加速度计中,这样的结构在三个方向各有一个,且做到了微米的尺寸,并配合相应的测量电路集成在一个芯片中(如图一所示),构成一个微机电系统(MEMS)。
陀螺仪
角速度测量的原理比加速度要复杂一些,因为涉及了科里奥里力(Coriolis Force)。所以我们先来说一下Coriolis Force。科里奥里力是由坐标系的转动与物体在动坐标系中的相对运动引起的,其本质是物体的惯性。
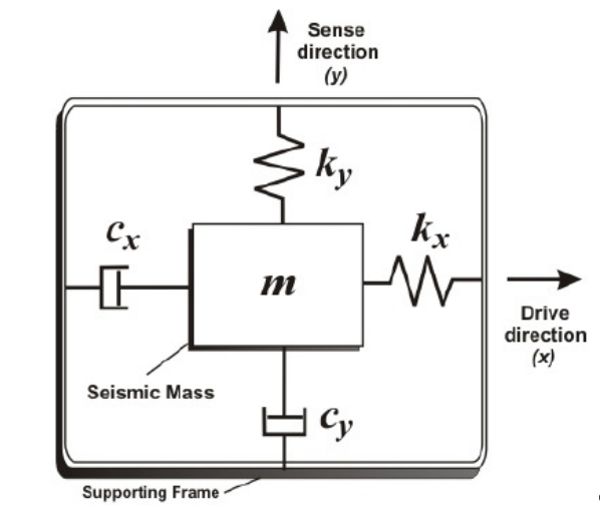
如果图示模块置于绝对静止的坐标系中,当在x方向施加一个驱动力使质量块运动时,根据牛顿第二定律,质量块只会在x方向上运动,而在y方向上不会运动。

但如果将图示模块置于一个旋转坐标系下,由于坐标系的旋转,使得当质量块沿x方向运动时,在y方向上会受到一个力,即科里奥里力F=-2mvω,从而使质量块沿y方向运动。地球上的很多自然现象,如热带气旋、季风带、河道两侧冲刷程度不同,都源于科里奥里力。
陀螺仪的物理实现如上图所示,外侧的蓝色与黄色部分为驱动电极,内部的红色与蓝色为测量电极。在模块的驱动方向施加正弦驱动电压,当模块发生旋转时,质量块在垂直方向受科里奥里力影响也会产生一个正弦运动,且正弦运动的幅值与平台的角速度成正比,通过垂直方向的电极测量出此幅值,便可以得到模块角速度。与三轴加速度计一样,这样的结构在三轴陀螺仪的三个方向上各有一个,从而测量出三个方向的角速度。
2. IMU姿态解算
现在我们能够从IMU中得到三轴的加速度和三轴的角速度,接下来就要从这些数据中解算出三个方向的角度。实际上,单独由加速度计或陀螺仪都可以解算出三轴的角度。
由加速度解算角度
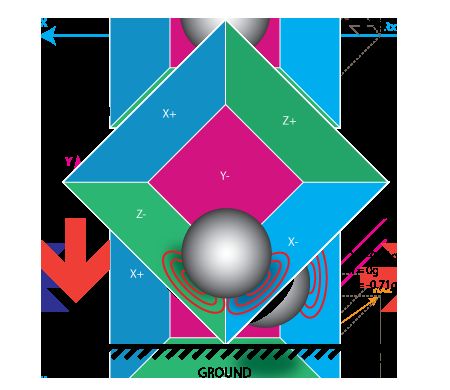
由于加速度计本质是测量力,所以在传感器静止的时候,测量的结果为重力加速度。当平台运动的加速度远小于重力加速度时,可认为传感器测量的结果全部为重力加速度,因此可以根据重力加速的在三轴分量的大小来解算出角度。
以上图为例,传感器沿y方向倾斜的角度为:
A n g l e A c c e l = a r c c o s a x − g Angle_{Accel} = arccos\frac{ax}{-g} AngleAccel=arccos−gax
由陀螺仪解算角度
由角速度解算角度很容易理解,当知道陀螺仪的初始角度时,对角速度进行积分就可以得到角度值。
A n g l e G y r o = A n g l e 0 + ∫ 0 t G y r o d t Angle_{Gyro}=Angle_0 + \int_0^t Gyro dt AngleGyro=Angle0+∫0tGyrodt
数据融合
现在我们可以从加速度和角速度分别解算出角度,但这两种方式都存在很大的问题。一方面由于加速度计容易受到振动的影响,噪声很大,所以解算角度的噪声也很大;另一方面虽然陀螺仪测量角速度的噪声不是很大,经过积分环节后噪声进一步被变小,但由于初始角度并不能准确得到,而且角速度存在零漂问题(即模块静止时角速度不完全为0,而是有一个偏置),经过积分后这个误差会被累积。
因此,两种方式解算出来的角度都无法直接使用,但我们可以采用数据融合的方法,把两种角度融合在一起,得到一个既没有累计误差、噪声又小的角度数据。
互补滤波
一阶互补滤波是最简单但却非常实用的数据融合算法,它把由加速度解算的角度和由角速度积分的角度按照一定比例加到一起,公式如下:
A n g l e = K ⋅ A n g l e a c c e l + ( 1 − K ) ⋅ ( A n g l e + ω ⋅ d t ) Angle = K\cdot Angle_{accel}+(1-K)\cdot (Angle + \omega\cdot dt) Angle=K⋅Angleaccel+(1−K)⋅(Angle+ω⋅dt)
其中参数K表示对加速度解算角度的置信程度,由于加速度的噪声很大,所以参数K一般很小,典型值为0.05,实际使用要根据效果来调整。
这样的互补滤波器可以看做是一个高通滤波和一个低通滤波的叠加:公式的第一项是为低通滤波部分,目的是滤除加速度的噪声;公式的第二项为高通滤波部分,目的是滤除角速度的直流偏置(零漂)。
Kalman滤波
互补滤波虽然简单实用易理解,但我们还有更好的算法来进行数据融合,比如Kalman滤波。关于Kalman滤波的原理,有一些非常好的论文和博客,感兴趣的同学可以移步这些网站:
Kalman先生1960年的论文
博客 How a Kalman filter works
上篇博客的中文版
论文 Understanding Kalman Filter
上篇论文的中文版
Kalman滤波的原理稍过复杂,这里并不打算深入讨论。但由于博客和论坛上关于用Kalman滤波融合加速度计和陀螺仪数据的建模方法介绍比较少,所以这里给出本问题状态空间方程的建立方法。
和一般系统的建模方法不同,本问题中的状态变量不是角度和角速度,而是角度和角速度的偏置:
S t a t e = [ A n g l e ( k ) G y r o b i a s ( k ) ] State = \begin{bmatrix} Angle(k) \\ Gyro_{bias}(k) \\ \end{bmatrix} State=[Angle(k)Gyrobias(k)]
状态空间模型考虑带控制量的形式,其中控制量为陀螺仪测量的角速度,观测方程中只有从加速度解算得到的角度,方程如下:
[ A n g l e ( k + 1 ) G y r o b i a s ( k + 1 ) ] = [ 1 − d t 0 1 ] [ A n g l e ( k ) G y r o b i a s ( k ) ] + [ d t 0 ] G y r o ( k ) + W ( k ) \begin{bmatrix} Angle(k+1) \\ Gyro_{bias}(k+1) \end{bmatrix} = \begin{bmatrix} 1 & -dt \\ 0 & 1 \end{bmatrix}\begin{bmatrix} Angle(k) \\ Gyro_{bias}(k) \end{bmatrix} + \begin{bmatrix} dt \\ 0 \end{bmatrix} Gyro(k) + W(k) [Angle(k+1)Gyrobias(k+1)]=[10−dt1][Angle(k)Gyrobias(k)]+[dt0]Gyro(k)+W(k)
A n g l e a c c e l ( k ) = [ 1 0 ] [ A n g l e ( k ) G y r o b i a s ( k ) ] + V ( k ) Angle_{accel}(k) =\begin{bmatrix} 1 & 0 \end{bmatrix} \begin{bmatrix} Angle(k) \\ Gyro_{bias}(k) \end{bmatrix} + V(k) Angleaccel(k)=[10][Angle(k)Gyrobias(k)]+V(k)
其中矩阵W和V分别为输入噪声矩阵和观测噪声矩阵,这两个矩阵的参数需要根据情况进行调整。对于本问题矩阵V的参数要比W的参数大很多,因为由加速度计观测角度的噪声很大。
3.使用IMU来测量关节角度
这里基于IMU设计了一套用来测量人体姿态的硬件,通过在身体每个肢段上放置一个IMU,测量每段肢体在空间中的姿态角,下位机使用单片机通过串口接收每个IMU模块的数据,然后通过CAN总线发送给上位机,上位机再解算出关节角度。制作的模块如下:
下图是测量大腿和小腿的数据,Matlab对接收的数据进行解算并实时显示出来。
下图是由IMU得到的行走状态下肢三关节的角度变化。初次实验采样频率设置的有点低,只有50HZ,所以波形看起来不太平滑。